Giải Toán 10 (Chân trời sáng tạo) Bài 3: Tích của một số với một vectơ
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 10 Bài 3: Tích của một số với một vectơ sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài 3. Mời các bạn đón xem:
Giải bài tập Toán 10 Bài 3: Tích của một số với một vectơ
1. Tích của một số với một vectơ và các tính chất
Lời giải:
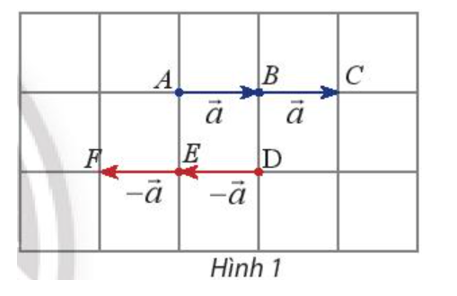
Vectơ →a+→a có hướng từ A sang C.
Vectơ (−→a)+(−→a) có hướng từ D sang F.
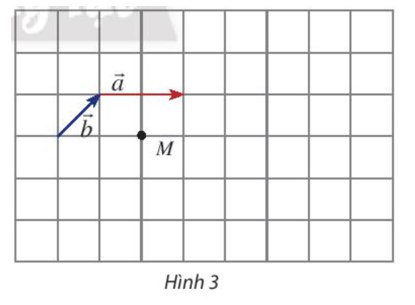
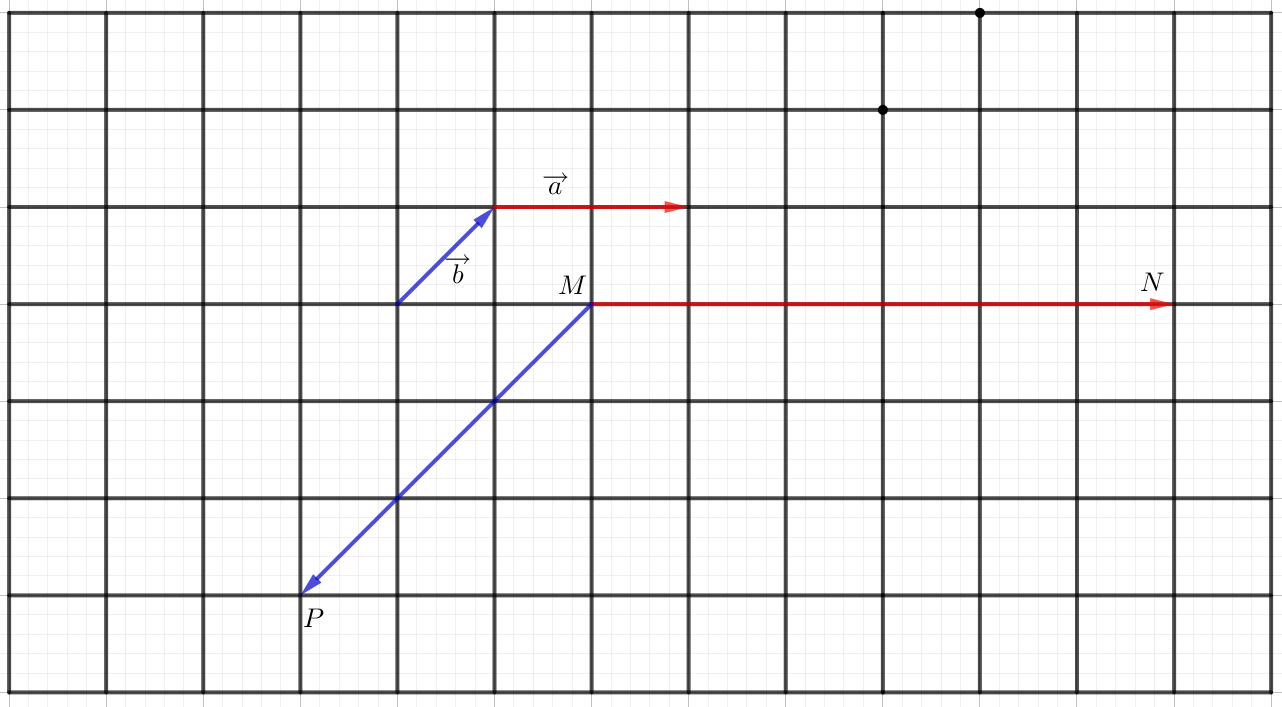
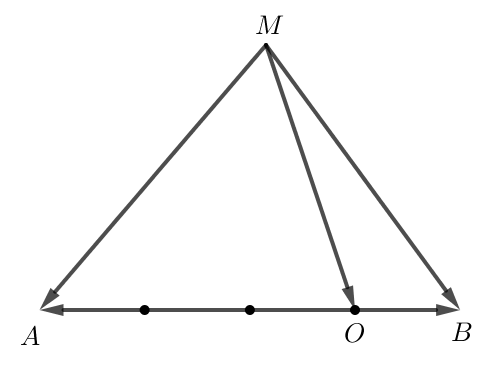
Thực hành 1 trang 95 Toán lớp 10 Tập 1: Cho hai vectơ →a,→b và một điểm M như Hình 3.
a) Hãy vẽ các vectơ →MN=3→a, →MP=−3→b .
b) Cho biết mỗi ô vuông có cạnh bằng 1. Tính: |3→b|, |−3→b|, |2→a+2→b|.
Lời giải:
a) Ta thấy 3 > 0 nên hai vectơ →MN và →a cùng hướng.
Do đó từ M kẻ đường thẳng d song song với đường thẳng a.
Trên đường thẳng d, về bên phải điểm M chọn điểm N sao cho MN = 6.
Khi đó →MN=3→a.
Do -3 < 0 nên hai vectơ →MP và →b ngược hướng.
Do đó từ M kẻ đường thẳng c song song với đường thẳng b.
Trên đường thẳng c, về bên trái điểm M chọn P sao cho MP = 3.
Khi đó →MP=−3→b.
Ta có hình vẽ như sau:
b) Ta thấy MP là độ dài cạnh huyền của 1 tam giác vuông cân có cạnh bằng 3.
Do đó MP = √32+32=3√2.
Ta thấy 3→b và −3→b là hai vectơ đối nên |3→b|=|−3→b|=|→MP|=3√2.
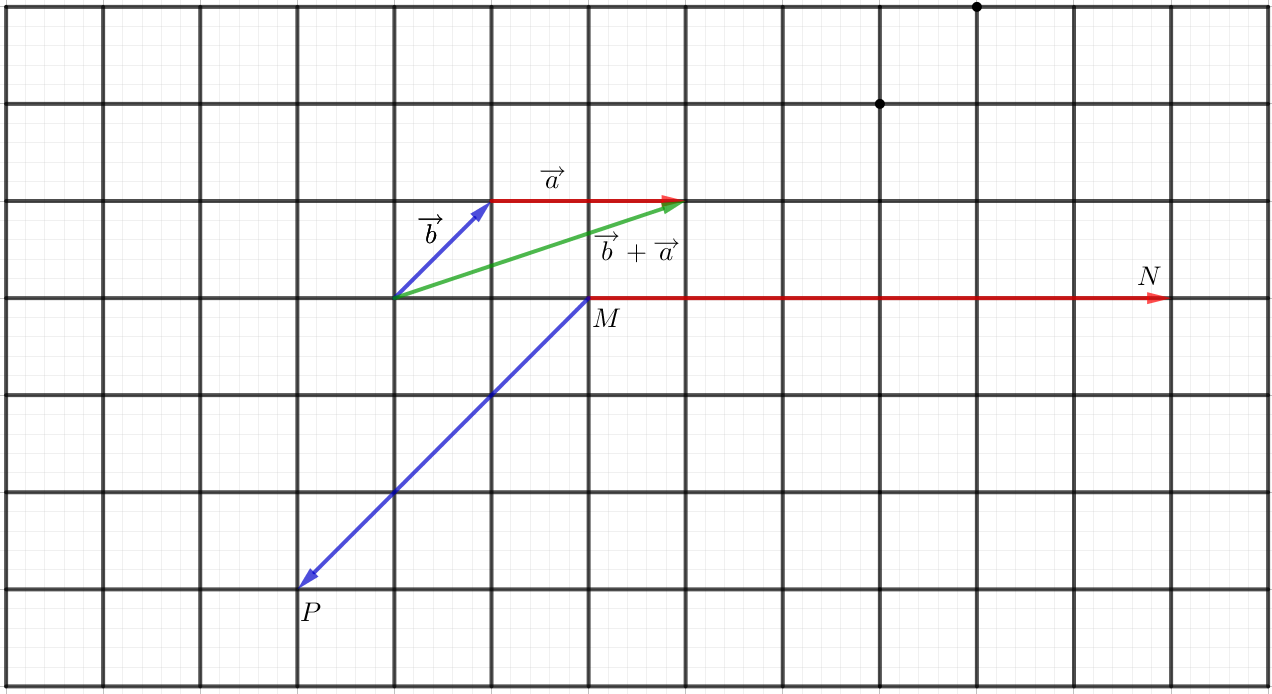
Ta thấy |→b+→a| là độ cạnh huyền của 1 tam giác vuông có độ dài 2 cạnh góc vuông lần lượt là 1 và 3.
Khi đó |→b+→a|=√32+12=√10.
Do đó |2→b+2→a|=|2→a+2→b|=2√10.
Vậy |3→b|=|−3→b|=3√2; |2→a+2→b|=2√10.
Lời giải:
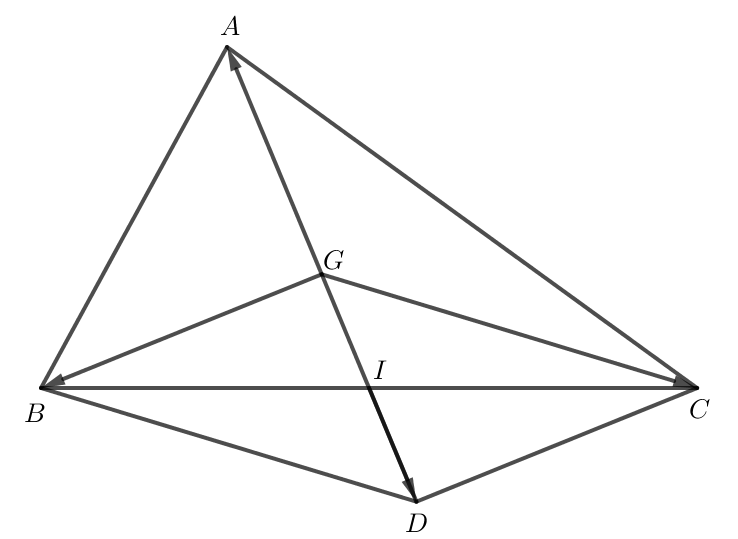
Phần thuận: G là trọng tâm của tam giác ABC thì →MA+→MB+→MC=3→MG.
Chứng minh:
Do G là trọng tâm của tam giác ABC nên →GA+→GB+→GC=→0.
Do đó →MG+→GA+→MG+→GB+→MG+→GC=3→MG hay →MA+→MB+→MC=3→MG.
Phần đảo: Tam giác ABC có →MA+→MB+→MC=3→MG thì G là trọng tâm của tam giác ABC.
Chứng minh:
→MA+→MB+→MC=3→MG
⇒→MG+→GA+→MG+→GB+→MG+→GC=3→MG
⇒→GA+→GB+→GC=→0
Dựng hình bình hành GBDC và gọi I là giao điểm của GD và BC.
Áp dụng quy tắc hình bình hành ta có →GB+→GC=→GD.
Mà →GA+→GB+→GC=→0 hay →GA+→GD=→0.
Do đó →GA=−→GD.
Khi đó |→GA|=|−→GD| hay GA = GD.
Hình bình hành GBDC có I là giao điểm hai đường chéo GD và BC nên I là trung điểm của BC và I là trung điểm của GD.
Do I là trung điểm của GD nên GI = 12GD = 12GA.
GI = 12GA nên AI = GI + GA = 12GA + GA = 32GA hay AG = 23AI.
Tam giác ABC có AI là đường trung tuyến, lại có AG = 23AI nên G là trọng tâm của tam giác ABC.
Vậy ta có điều phải chứng minh.
Lời giải:
Ta thấy hai vectơ →a và →b ngược hướng và |→b|=50; |→a|=20.
⇒|→b|=52|→a|.
Vậy →b=−52→a.
2. Điều kiện để hai vectơ cùng phương
Lời giải:
Ta thấy với →b khác →0 thì |→a||→b| ≥ 0.
Do đó hai vectơ →c và →b là hai vectơ cùng hướng.
Mà →a và →b là hai vectơ cùng phương nên hai vectơ →a và →c cùng hướng khi hai vectơ →a và →b cùng hướng; hai vectơ →a và →c ngược hướng khi hai vectơ →a và →b ngược hướng.
Do →c=|→a||→b|.→b nên |→c|=||→a||→b|.→b|=|→a||→b|.|→b|=|→a|.
Do đó độ dài của hai vectơ →a và →c bằng nhau.
Lời giải:
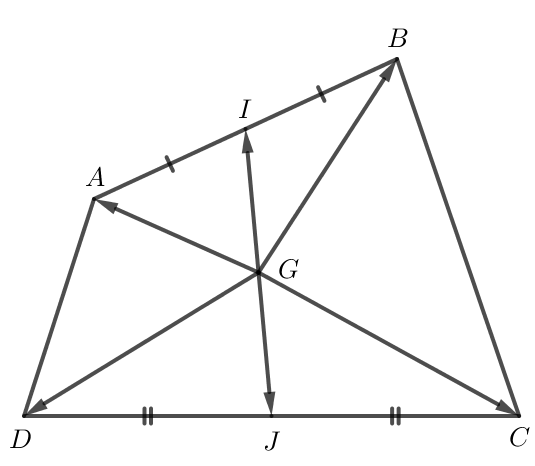
Do I là trung điểm của AB nên →GA+→GB=2→GI.
Do J là trung điểm của CD nên →GC+→GD=2→GJ.
Do đó →GA+→GB+→GC+→GD=2→GI+2→GJ hay →GI+→GJ=→0.
Do →GI+→GJ=→0 nên G là trung điểm của IJ.
Vậy I, G, J thẳng hàng.
Bài tập
Lời giải:
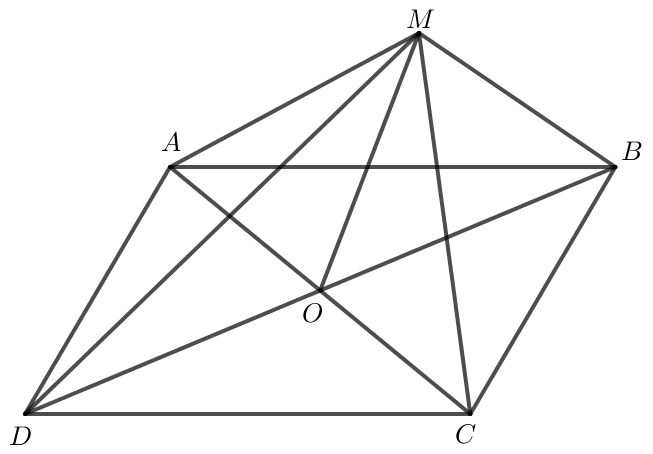
a) Hình bình hành ABCD có O là giao điểm hai đường chéo nên OA = OC, OB = OD.
Khi đó →OA và →OC là hai vectơ đối, →OB và →OD là hai vectơ đối.
Do đó →OA+→OB+→OC+→OD=→0.
Ta có →MA+→MB+→MC+→MD=→MG+→GA+→MG+→GB+→MG+→GC+→MG+→GD
=4→MG+(→GA+→GB+→GC+→GD)
=4→MG
Vậy →MA+→MB+→MC+→MD=4→MO.
b) Áp dụng quy tắc hình bình hành ta có →AB+→AD=→AC.
Do đó →AB+→AD+→AC=→AC+→AC hay →AB+→AC+→AD=2→AC.
Vậy →AB+→AC+→AD=2→AC.
Lời giải:
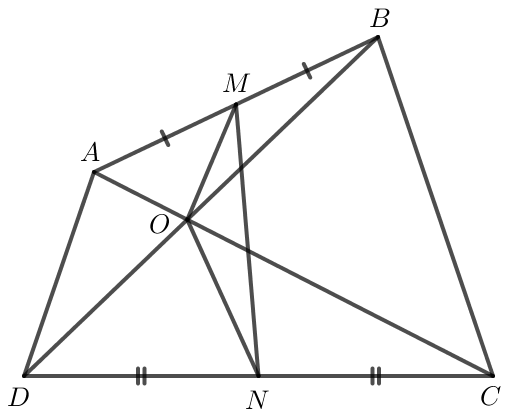
a) Gọi O là giao điểm hai đường chéo của tứ giác ABCD.
Do M là trung điểm của AB nên →OA+→OB=2→OM.
Do đó →AO+→BO=2→MO.
Do N là trung điểm của CD nên →OC+→OD=2→ON.
Do đó →AO+→BO+→OC+→OD=2→MO+2→ON.
hay →AO+→OC+→BO+→OD=2→MN.
Do đó →AC+→BD=2→MN.
b) Ta có →AD=→AC+→CD
Do đó →BC+→AD=→BC+→AC+→CD=→AC+(→BC+→CD)=→AC+→BD.
Vậy →AC+→BD=→BC+→AD.
Lời giải:
Do →MA+4→MB=→0 nên →MA=−4→MB do đó |→MA|=|−4||→MB|=4|→MB| hay MA = 4MB.
Ta thấy -4 < 0 nên hai vectơ →MA và →MB ngược hướng.
Do đó A và B nằm ở hai phía so với điểm M.
Ta thực hiện vẽ như sau:
Bước 1. Vẽ đường thẳng d, trên đường thẳng d xác định hai điểm M và B.
Bước 2. Trên đường thẳng d, xác định điểm A sao cho A và B nằm ở hai phía so với điểm M thỏa mãn MA = 4MB.
Ta có hình vẽ như sau:
Lời giải:
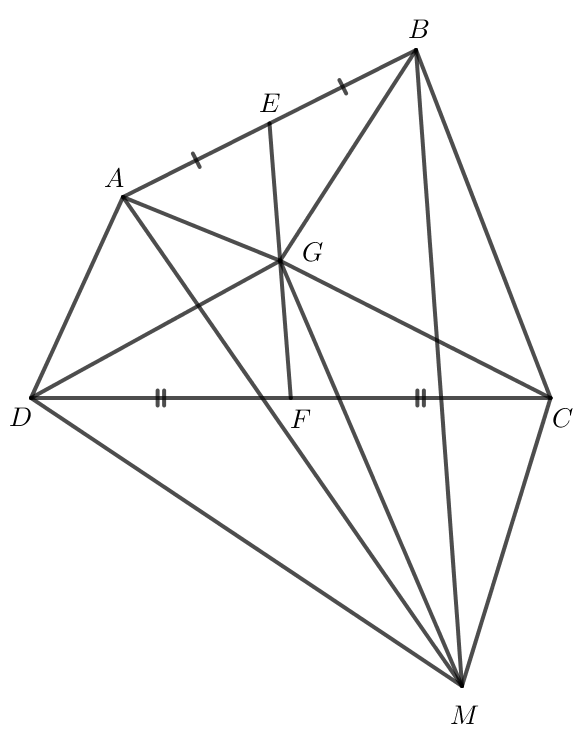
Do E là trung điểm của AB nên →GA+→GB=2→GE.
Do F là trung điểm của CD nên →GC+→GD=2→GF.
Do G là trung điểm của EF nên →GE+→GF=→0.
Do đó →GA+→GB+→GC+→GD=2→GE+2→GF=2(→GE+→GF)=→0.
Ta có →MA+→MB+→MC+→MD=→MG+→GA+→MG+→GB+→MG+→GC+→MG+→GD
=4→MG+(→GA+→GB+→GC+→GD)
=4→MG
Vậy →MA+→MB+→MC+→MD=4→MG.
Lời giải:
Ta thấy hai vectơ →a và →b ngược hướng và |→a| = 600, |→b| = 800.
Do đó |→b|=800600|→a|=43|→a| hay b = 43a.
Mà hai vectơ →a và →b ngược hướng nên →b=−43→a.
Vậy →b=−43→a.
Bài 6 trang 97 Toán lớp 10 Tập 1: Cho hai điểm phân biệt A và B.
a) Xác định điểm O sao cho →OA+3→OB=→0.
b) Chứng minh rằng với mọi điểm M, ta có →MA+3→MB=4→MO.
Lời giải:
a) Do →OA+3→OB=→0 nên →OA=−3→OB do đó |→OA|=|−3||→OB|=3|→OB| hay OA = 3OB.
Ta thấy -3 < 0 nên hai vectơ →OA và →OB ngược hướng.
Do đó A và B nằm ở hai phía so với điểm O.
Ta thực hiện vẽ như sau:
Bước 1. Vẽ đường thẳng d, trên đường thẳng d xác định hai điểm O và B.
Bước 2. Trên đường thẳng d, xác định điểm A sao cho A và B nằm ở hai phía so với điểm O thỏa mãn OA = 3OB.
Ta có hình vẽ như sau:
b)
Ta có →MA+3→MB=→MO+→OA+3(→MO+→OB)=4→MO+→OA+3→OB=4→MO.
Vậy →MA+3→MB=4→MO.
Bài 7 trang 97 Toán lớp 10 Tập 1: Cho tam giác ABC.
a) Xác định các điểm M, N, P thỏa mãn: →MB=12→BC, →AN=3→NB, →CP=→PA.
b) Biểu thị mỗi vectơ →MN, →MP theo hai vectơ →BC, →BA.
c) Chứng minh ba điểm M, N, P thẳng hàng.
Lời giải:
a) Do →MB=12→BC nên hai vectơ →MB và →BC cùng hướng.
Do đó M và C nằm ở hai phía so với điểm B sao cho MB = 12BC.
Do →AN=3→NB nên →AN+→NB=4→NB hay →AB=4→NB.
Do đó A và N nằm cùng phía so với điểm B sao cho NB = 14AB.
Do →CP=→PA nên →CP+→PA=2→PA hay →CA=2→PA.
Do đó P và C nằm cùng phía so với điểm A sao cho PA = 12CA.
Ta có hình vẽ sau:
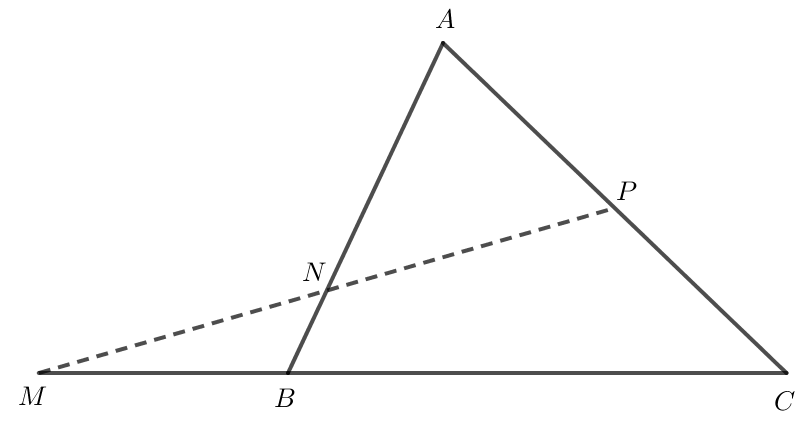
b) Ta có →MN=→BN−→BM.
Do →AN=3→NB nên →NA=3→BN⇒→BN+→NA=4→BN hay →BA=4→BN.
Do đó →BN=14→BA.
Do →MB=12→BC nên →BM=−12→BC.
Do đó →MN=→BN−→BM=14→BA+12→BC.
Ta có →MP=→BP−→BM.
Do đó P và C nằm cùng phía so với điểm A và PA = 12CA nên P là trung điểm của CA.
Do đó →BA+→BC=2→BP⇒→BP=12(→BA+→BC).
Do đó →MP=→BP−→BM=12(→BA+→BC)+12→BC=12→BA+→BC.
Ta thấy →MN=14→BA+12→BC; →MP=12→BA+→BC nên →MP=2→MN.
Do đó M, N, P thẳng hàng và N là trung điểm của MP.
