Giải bài tập Toán 10 Bài 2: Hàm số bậc hai

Khởi động trang 49 Toán lớp 10 Tập 1: Các hàm số này có chung đặc điểm gì?

y = ax²;

y = a(x – m)(x – n);

y = ax² + bx;

y = a(x – h)² + k;

y = ax² + bx + c.

Lời giải:

Ta có:

y = a(x – m)(x – n) = a(x² – xn – mx + mn) = ax² – anx – amx + amn = ax² – (n + m)ax + amn

y = a(x – h)² + k = a(x² – 2xh + h²) + k = ax² – 2ahx + ah² + k

y = ax²                            

y = ax² + bx          

y = ax² + bx + c

Tất cả các hàm số trên đều có lũy thừa bậc cao nhất của ẩn x là bậc hai.

1. Hàm số bậc hai

Khám phá 1 trang 49 Toán lớp 10 Tập 1: Khai triển biểu thức của các hàm số sau và sắp xếp theo thứ tự lũy thừa của x giảm dần (nếu có thể). Hàm số nào có lũy thừa bậc cao nhất của x là bậc hai?

a) y = 2x(x – 3);

b) y = x(x² + 2) – 5;

c) y = -5(x + 1)(x – 4).

Lời giải:

a) y = 2x(x – 3) = 2x² – 6x

Lũy thừa bậc cao nhất của x là bậc hai.

b) y = x(x² + 2) – 5 = x³ + 2x – 5.

Lũy thừa bậc cao nhất của x là bậc ba.

c) y = –5(x + 1)(x – 4) = –5(x² – 4x + x – 4) = –5.(x² – 3x – 4) = –5x² + 15x + 20

Lũy thừa bậc cao nhất của x là bậc hai.

Vậy các hàm số có lũy thừa bậc cao nhất của x là bậc hai là:

y = 2x(x – 3)

y = –5(x + 1)(x – 4).

Thực hành 1 trang 49 Toán lớp 10 Tập 1: Hàm số nào trong các hàm số đã cho ở hoạt động khám phá 1 là hàm số bậc hai?

Lời giải:

Các hàm số bậc hai là:

y = 2x(x – 3) = 2x² – 6x

y = –5(x + 1)(x – 4) = –5(x² – 4x + x – 4) = –5.(x² – 3x – 4) = –5x² + 15x + 20

2. Đồ thị hàm số bậc hai

Khám phá 2 trang 49 Toán lớp 10 Tập 1: a) Xét hàm số: y = f(x) = x² – 8x + 19 = (x – 4)² + 3 có bảng giá trị:

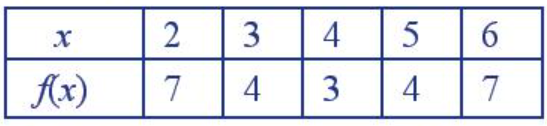
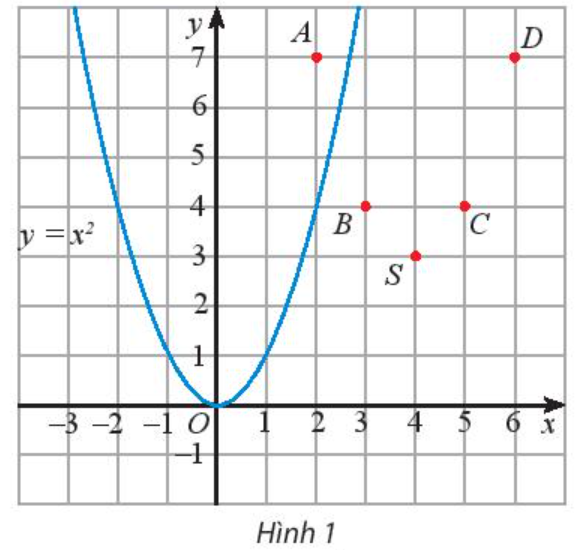
Trên mặt phẳng tọa độ, ta có các điểm (x; f(x)) với x thuộc bảng giá trị đã cho (Hình 1).

Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị của hàm số y = x² trên Hình 1.

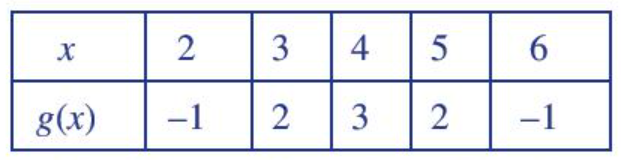
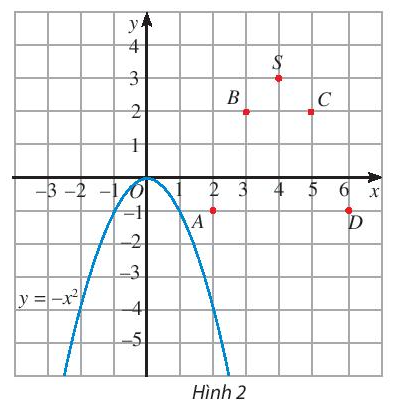
b) Tương tự, xét hàm số: y = g(x) = - x² + 8x – 13 = - (x – 4)² + 3 có bảng giá trị:

Trên mặt phẳng tọa độ, ta có các điểm (x; g(x)) với x thuộc bảng giá trị đã cho (Hình 2).

Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số y = - x² trên Hình 2.

Lời giải:

a)

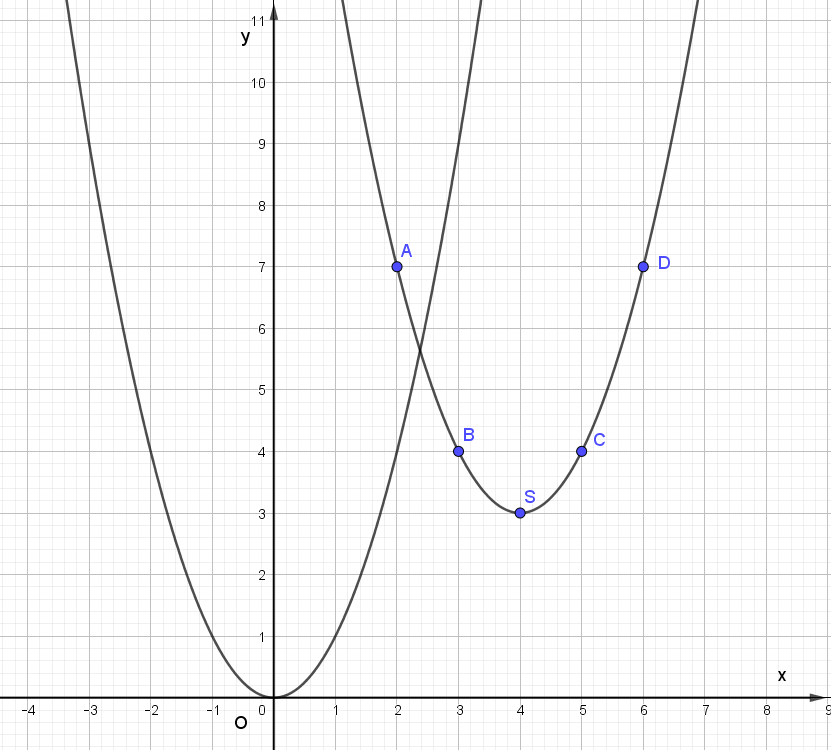
Ta thấy đường cong đi qua các điểm A, B, S, C, D có hình dạng giống với đồ thị của hàm số y = x² trên Hình 1.

b)

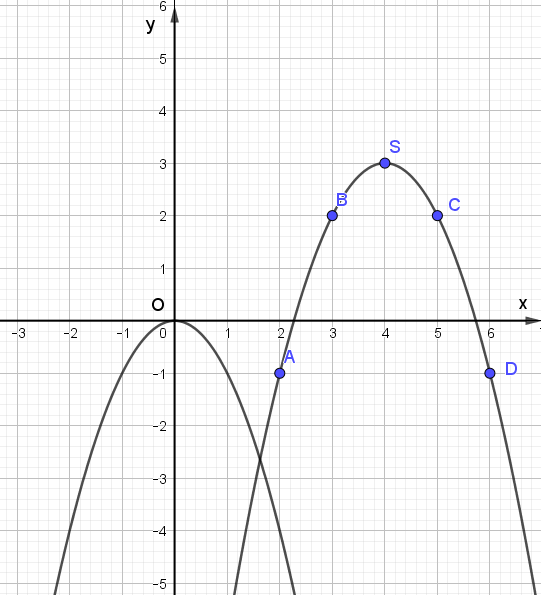
Ta thấy đường cong đi qua các điểm A, B, S, C, D có hình dạng giống với đồ thị của hàm số y = –x² trên Hình 2.

Thực hành 2 trang 52 Toán lớp 10 Tập 1: Vẽ đồ thị hàm số y = x² – 4x + 3 rồi so sánh đồ thị hàm số này với đồ thị hàm số ở ví dụ 2a. Nếu nhận xét về hai đồ thị này.

Lời giải:

Xét hàm số y = f(x) = x² – 4x + 3, ta có:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = x² – 4x + 3 là một parabol (P):

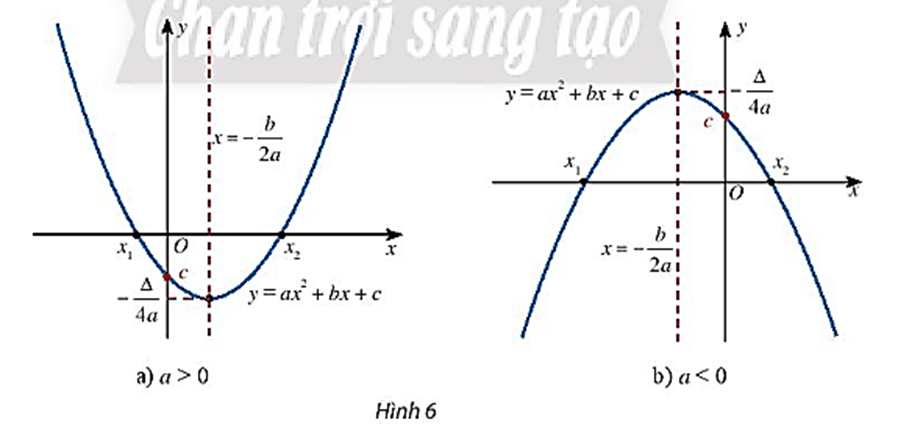
– Có đỉnh S với hoành độ x_S = 2, tung độ y_S­ = – 1;

– Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

– Bề lõm quay lên trên vì a = 1 > 0;

– Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).

– Ngoài ra, phương trình x² – 4x + 3 = 0 có hai nghiệm phân biệt x₁ = 1 và x₂ = 3 nên đồ thị hàm số cắt trục hành tại hai điểm có tọa độ (1; 0) và (3; 0).

Ta vẽ được đồ thị như hình dưới:

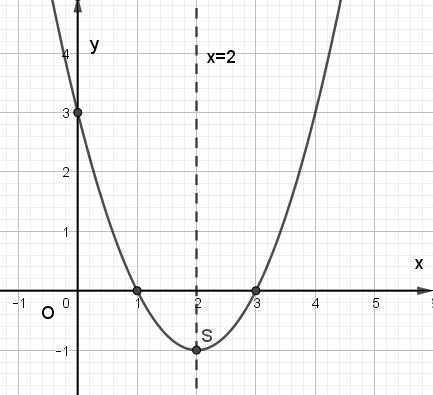
Ta thấy đồ thị hàm số y = f(x) = x² – 4x + 3 có hình dạng đảo ngược của đồ thị hàm số trong Ví dụ 2a. Chúng có đỉnh đối xứng nhau qua Ox, chung hai giao điểm với trục Ox, giao điểm với Oy của chúng đối xứng nhau qua Ox và bề lõm có hướng ngược nhau.

3. Sự biến thiên của hàm số bậc hai

Khám phá 3 trang 52 Toán lớp 10 Tập 1: Từ đồ thị của hàm số bậc hai cho ở hai hình sau, tìm khoảng đồng biến và nghịch biến của hàm số trong mỗi trường hợp.

Lời giải:

a) Trường hợp a > 0, ta có:

Trong khoảng $\left(-\infty ;-\frac{b}{2a}\right)$, ta thấy đồ thị hàm số đi xuống từ trái sang phải, do đó, hàm số nghịch biến trên khoảng $\left(-\infty ;-\frac{b}{2a}\right)$.

Trong khoảng $\left(-\frac{b}{2a};+\infty \right)$, ta thấy đồ thị hàm số đi lên từ trái sang phải, do đó, hàm số đồng biến trên khoảng $\left(-\frac{b}{2a};+\infty \right)$.

b) Trường hợp a < 0, ta có:

Trong khoảng $\left(-\infty ;-\frac{b}{2a}\right)$, ta thấy đồ thị hàm số đi lên từ trái sang phải, do đó, hàm số đồng biến trên khoảng $\left(-\infty ;-\frac{b}{2a}\right)$.

Trong khoảng $\left(-\frac{b}{2a};+\infty \right)$, ta thấy đồ thị hàm số đi xuống từ trái sang phải, do đó, hàm số nghịch biến trên khoảng $\left(-\frac{b}{2a};+\infty \right)$.

Thực hành 3 trang 53 Toán lớp 10 Tập 1: Tìm khoảng đồng biến, khoảng nghịch biến của hàm số y = 2x² – 6x + 11. Hàm số có thể đạt giá trị bằng – 1 không? Tại sao?

Lời giải:

Xét hàm số y = 2x² – 6x + 11.

Đỉnh S có tọa độ: $x_S=\frac{-b}{2a}=\frac{-(-6)}{2.2}=\frac{3}{2};y_S=2.{\left(\frac{3}{2}\right)}^2-6.\frac{3}{2}+11=\frac{13}{2}$.

Hay $S\left(\frac{3}{2};\frac{13}{2}\right)$.

Vì hàm số bậc hai có a = 2 > 0 nên ta có bảng biến thiên sau:

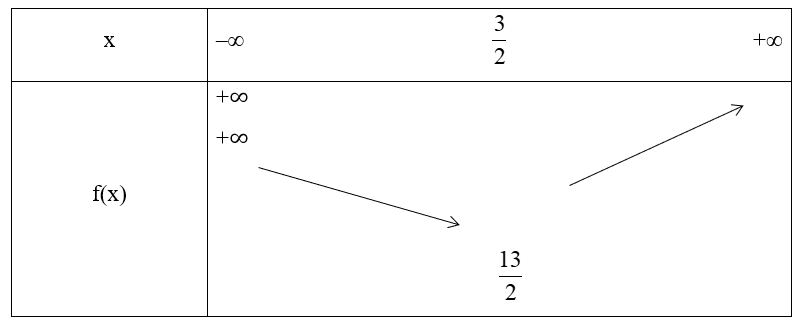
Khoảng đồng biến của hàm số là $\left(\frac{3}{2};+\infty \right)$ và khoảng nghịch biến của hàm số là $\left(-\infty ;\frac{3}{2}\right)$.

Hàm số đạt giá trị nhỏ nhất bằng $\frac{13}{2}$ khi $x=\frac{3}{2}$.

Do đó, hàm số không thể đạt giá trị bằng –1.

4. Ứng dụng của hàm số bậc hai

Vận dụng trang 55, 56 Toán lớp 10 Tập 1: Trong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được cho là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên).

a) Vận tốc xuất phát của cầu là 12m/s.

b) Vị trí phát cầu cách mặt đất là 1,3m.

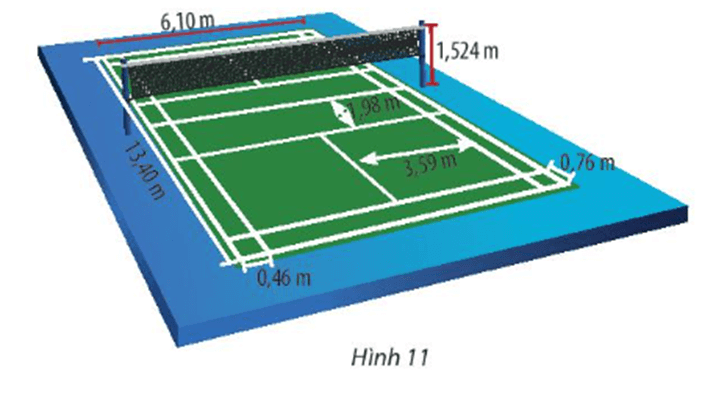
Lưu ý: Các thông số về sân cầu lông được cho trong Hình 11.

Lời giải:

a) Coi người chơi cầu lông có khuynh hướng phát cầu với góc 30 độ so với mặt đất, cầu rời mặt vợt ở độ cao 0,7 m so với mặt đất và vận tốc ban đầu của cầu là 12 m/s (bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng thẳng đứng).

Chọn hệ trục tọa độ như hình vẽ (vị trí rơi của cầu thuộc trục hoành và vị trí cầu rời mặt vợt thuộc trục tung).

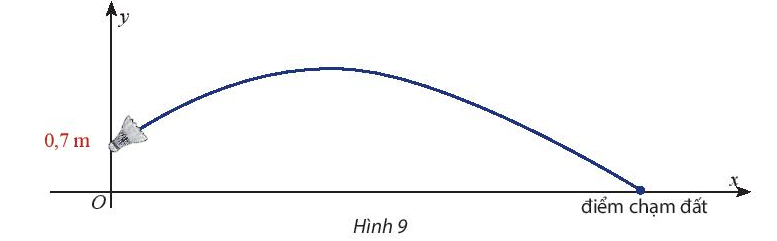
Với g = 9,8 m/s², góc phát cầu α = 30°, vận tốc ban đầu v₀ = 12 m/s, phương trình quỹ đạo của cầu là:$y=\frac{-9,8.x^2}{{2.12}^2.co{s}^2{30}^o}+\tan {30}^o.x+0,7=-\frac{49}{1080}{x}^2+\frac{\sqrt{3}}{3}x+0,7$

(với x ≥ 0).

Khi x = 4, ta có $y=-\frac{49}{1080}{.4}^2+\frac{\sqrt{3}}{3}.4+0,7\approx 2,283$> 1,524.

Như vậy, cầu đã vượt qua lưới. Điểm rơi của cầu là giao điểm của parabol và trục hoành nên giải phương trình:

$-\frac{49}{1080}{x}^2+\frac{\sqrt{3}}{3}x+0,7=0$ ta được: x_1­ ≈ 13,84 và x₂ ≈ –1,11.

Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 13,84 m.

Khoảng cách từ lưới đến điểm cầu rơi là: 13,84 – 4 = 9,84 (m)

Dựa vào các thông số về sân cầu lông đơn ta thấy:

Điểm biên trong cách lưới 1,98 m và điểm biển ngoài cách lưới là:

$\frac{13,40}{2}-0,76=5,94$ (m)

Ta có: 9,84 m > 5,94 m. Do đó, cầu bay ra khỏi biên ngoài nên lần phát cầu bị hỏng.

b)

Coi người chơi cầu lông có khuynh hướng phát cầu với góc 30 độ so với mặt đất, cầu rời mặt vợt ở độ cao 1,3 m so với mặt đất và vận tốc ban đầu của cầu là 8 m/s (bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng thẳng đứng).

Chọn hệ trục tọa độ như hình vẽ (vị trí rơi của cầu thuộc trục hoành và vị trí cầu rời mặt vợt thuộc trục tung).

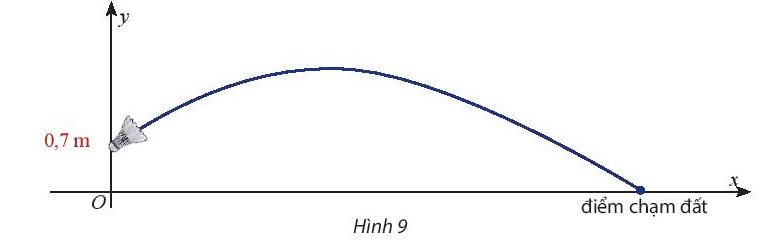
Với g = 9,8 m/s², góc phát cầu α = 30^o, vận tốc ban đầu v₀ = 8 m/s, phương trình quỹ đạo của cầu là:

 $y=\frac{-9,8.x^2}{{2.8}^2.co{s}^2{30}^o}+\tan {30}^o.x+1,3=-\frac{4,9}{48}{x}^2+\frac{\sqrt{3}}{3}x+1,3$ (với x ≥ 0)

Khi x = 4, ta có $y=\frac{4,9}{48}{.4}^2+\frac{\sqrt{3}}{3}.4+1,3\approx 1,976$ > 1,524 .

Như vậy, cầu đã vượt qua lưới. Điểm rơi của cầu là giao điểm của parabol và trục hoành nên giải phương trình:

 $-\frac{4,9}{48}{x}^2+\frac{\sqrt{3}}{3}x+1,3=0$ ta được: x1­ ≈ 7,38 và x2 ≈ –1,725.

Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 7,38 m.

Khoảng cách từ lưới đến điểm cầu rơi là: 7,38 – 4 = 3,38 (m)

Dựa vào các thông số về sân cầu lông đơn ta thấy:

Điểm biên trong cách lưới 1,98 m và điểm biển ngoài cách lưới là:

 $\frac{13,40}{2}-0,76=5,94$ (m)

Ta có: 1,98 m < 3,38 m < 5,94 m. Do đó, cầu nằm trong biên nên lần phát cầu hợp lệ.

Bài tập

Bài 1 trang 56 Toán lớp 10 Tập 1: Hàm số nào sau đây là hàm số bậc hai?

a) y = 9x² + 5x + 4;

b) y = 3x³ + 2x + 1;

c) y = -4(x + 2)³ + 2(2x³ + 1) + 5;

d) y = 5x² +  $\sqrt{x}$ + 2.

Lời giải:

a) y = 9x² + 5x + 4

Đây là hàm số bậc hai bởi nó có dạng ax² + bx + c = 0 với a = 9 ≠ 0, b = 5, c = 4 là các số thực.

b) y = 3x³ + 2x + 1

Đây không phải là hàm số bậc hai bởi nó không có dạng ax² + bx + c = 0.

c) y = –4(x + 2)³ + 2(2x³ + 1) + 5 = –4(x³ + 6x² + 12x + 8) + 4x³ + 2 + 5

= –4x³ – 24x² – 48x – 32 + 4x³ + 2 + 5

= – 24x² – 48x – 25

Đây là hàm số bậc hai bởi nó có dạng ax² + bx + c = 0 với a = –24 ≠ 0, b = –48, c = –25 là các số thực.

d) $y=5x^2+\sqrt{x}+2$

Đây không phải là hàm số bậc hai bởi nó không có dạng ax² + bx + c = 0.

Bài 2 trang 56 Toán lớp 10 Tập 1: Tìm điều kiện của m để mỗi hàm số sau là hàm số bậc hai.

a) y = mx⁴ + (m + 1)x² + x + 3;

b) y = (m – 2)x³ + (m – 1)x² + 5.

Lời giải:

a) Hàm số y = mx⁴ + (m + 1)x² + x + 3 là hàm số bậc hai khi và chỉ khi$\left\{\begin{array}{l}m=0\\ m+1\ne 0\end{array}\right.\iff \left\{\begin{array}{l}m=0\\ m\ne -1\end{array}\right.\iff m=0$

Vậy khi m = 0 thì hàm số y = mx⁴ + (m + 1)x² + x + 3 là hàm số bậc hai.

b) Hàm số y = (m – 2)x³ + (m – 1)x² + 5 là hàm số bậc hai khi và chỉ khi$\left\{\begin{array}{l}m-2=0\\ m-1\ne 0\end{array}\right.\iff \left\{\begin{array}{l}m=2\\ m\ne 1\end{array}\right.\iff m=2$

Vậy khi m = 2 thì hàm số y = (m – 2)x³ + (m – 1)x² + 5 là hàm số bậc hai.

Bài 3 trang 56 Toán lớp 10 Tập 1: Lập bảng biến thiên của hàm số y = x² + 2x + 3. Hàm số này có giá trị lớn nhất hay nhỏ nhất? Tìm giá trị đó.

Lời giải:

Xét hàm số y = x² + 2x + 3 ta có:

Đỉnh S có hoành độ là: $x_S=\frac{-b}{2a}=\frac{-2}{2}=-1$, có tung độ là: yS = (–1)2 + 2.(–1) + 3 = 2

Hay điểm S(– 1; 2).

Có a = 1 > 0, bề lõm hướng lên trên, nên có bảng biến thiên như sau:

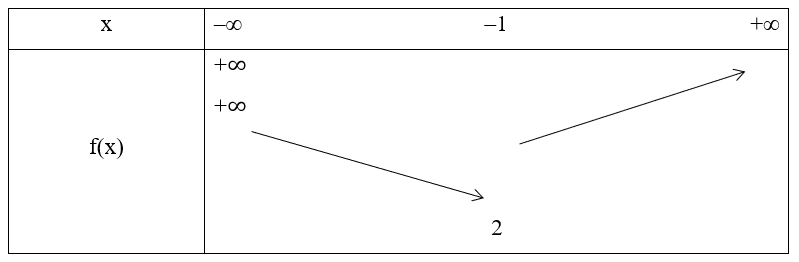
Vậy hàm số đạt giá trị nhỏ nhất là 2 tại x = – 1.

Bài 4 trang 56 Toán lớp 10 Tập 1: Cho hàm số bậc hai y = f(x) = ax² + bx + c có f(0) = 1, f(1) = 2, f(2) = 5.

a) Hãy xác định giá trị của các hệ số a, b, c.

b) Xác định tập giá trị và khoảng biến thiên của hàm số.

Lời giải:

a)

Theo đề bài ta có:

f(0) = a.0² + b.0 + c = 1 ⇒ c = 1

f(1) = a.1² + b.1 + c = a + b + 1 = 2 ⇒ a + b = 2 – 1 = 1 (2)

f(2) = a.2² + b.2 + c = 4a + 2b + 1 = 5 ⇒ 4a + 2b = 5 – 1 = 4 (3)

Từ (2) và (3) ta có hệ phương trình:$\left\{\begin{array}{l}a+b=1\\ 4a+2b=4\end{array}\right.\iff \left\{\begin{array}{l}2b=0\\ a+b=1\end{array}\right.\iff \left\{\begin{array}{l}b=0\\ a+0=1\end{array}\right.\iff \left\{\begin{array}{l}a=1\\ b=0\end{array}\right.$

Vậy a = 1, b = 0, c = 1.

b) Với a = 1, b = 0, c = 1.

Ta có hàm số: y = x² + 1

Đỉnh S của đồ thị có hoành độ là: $x_S=\frac{-b}{2a}=\frac{-0}{2.1}=0$ và yS = 02 + 1 = 1.

Hay điểm S(0; 1).

Do a = 1 > 0 nên bề lõm của đồ thị hướng lên, ta có bảng biến thiên như sau:

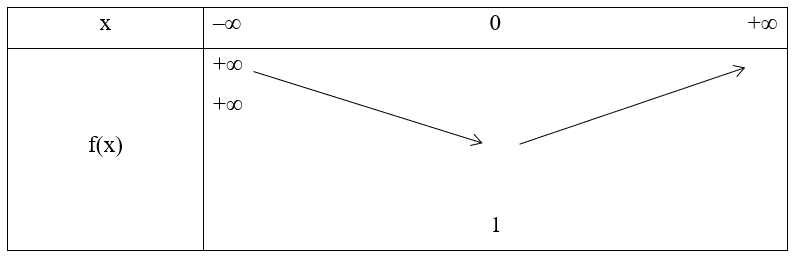
Vậy hàm số đồng biến trên khoảng (0; +∞) và nghịch biến trên khoảng (–∞; 0). Giá trị nhỏ nhất của hàm số là 1 tại x = 0. Tập giá trị của hàm số là T = [1; +∞).

Bài 5 trang 56 Toán lớp 10 Tập 1: Cho hàm số y = 2x² + x + m. Hãy xác định giá trị của m để hàm số đạt giá trị nhỏ nhất bằng 5.

Lời giải:

Xét hàm số y = 2x² + x + m có:

Đỉnh S có hoành độ là $x_S=\frac{-b}{2a}=\frac{-1}{2.2}=\frac{-1}{4}$ và tung độ là $y_S=2.{\left(\frac{-1}{4}\right)}^2-\frac{1}{4}+m=-\frac{1}{8}+m$

Ta có, a = 2 > 0, đồ thị có bề lõm hướng lên trên, ta có bảng biến thiên như sau:

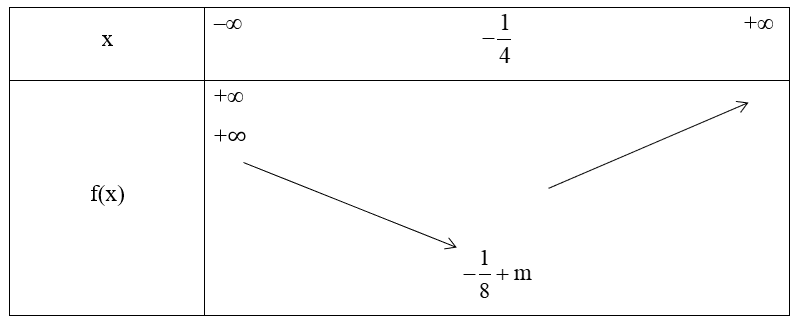
Vậy giá trị nhỏ nhất của hàm số là $-\frac{1}{8}+m$ tại $x=-\frac{1}{4}$

Để hàm số đạt giá trị nhỏ nhất bằng 5 khi và chỉ khi $-\frac{1}{8}+m=5\iff m=\frac{41}{8}$

Vậy $m=\frac{41}{8}$ thỏa mãn yêu cầu đề bài.

Bài 6 trang 56 Toán lớp 10 Tập 1: Vẽ đồ thị các hàm số sau:

a) y = 2x² + 4x – 1;

b) y = -x² + 2x + 3;

c) y = -3x² + 6x;

d) y = 2x² – 5.

Lời giải:

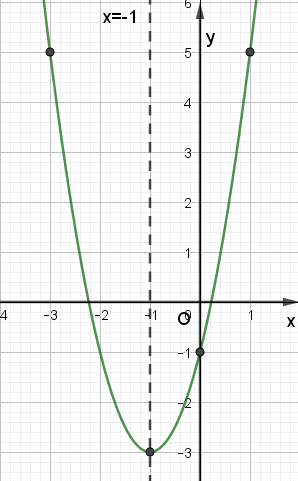
a) Xét hàm số y = 2x² + 4x – 1, ta có:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = 2x² + 4x – 1 là một parabol (P):

– Có đỉnh S với hoành độ x_S = –1, tung độ y_S­ = –3;

– Có trục đối xứng là đường thẳng x = –1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

– Bề lõm quay lên trên vì a = 2 > 0;

– Cắt trục tung tại điểm có tung độ bằng –1, tức là đồ thị đi qua điểm có tọa độ (0; –1);

– Ngoài ra, đồ thị hàm số y = f(x) còn đi qua hai điểm (–3; 5) và (1; 5).

Ta vẽ được đồ thị như hình dưới:

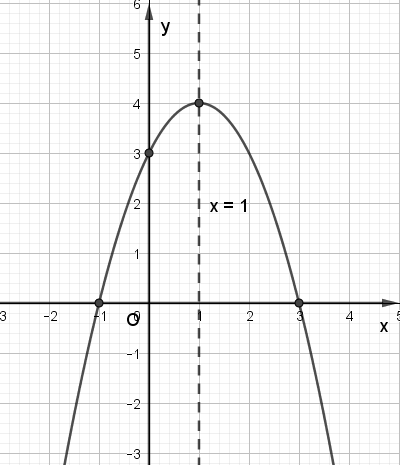
b) Xét hàm số y = –x² + 2x + 3, ta có:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –x² + 2x + 3 là một parabol (P):

– Có đỉnh S với hoành độ x_S = 1, tung độ y_S­ = 4;

– Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

– Bề lõm quay xuống dưới vì a = – 1 < 0;

– Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3);

– Ngoài ra, phương trình –x² + 2x + 3 = 0 có hai nghiệm phân biệt là x₁ = –1, x₂ = 3. Do đó, đồ thị còn đi qua hai điểm (–1; 0), (3; 0).

Ta vẽ được đồ thị như hình dưới:

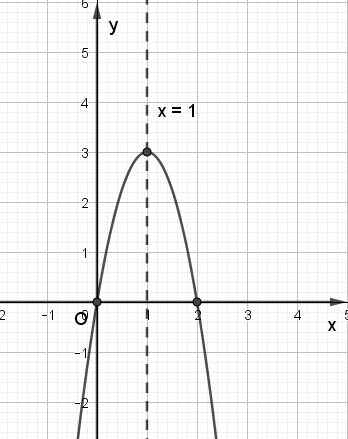
c) Xét hàm số y = –3x² + 6x, ta có:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = –3x² + 6x là một parabol (P):

– Có đỉnh S với hoành độ x_S = 1, tung độ y_S­ = 3;

– Có trục đối xứng là đường thẳng x = 1 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

– Bề lõm quay xuống dưới vì a < 0;

– Cắt trục tung tại điểm có tung độ bằng 0, tức là đồ thị đi qua điểm có tọa độ (0; 0);

– Ngoài ra, phương trình –3x² + 6x = 0 có hai nghiệm phân biệt là x₁ = 0, x₂ = 2. Do đó, đồ thị còn đi qua điểm (2; 0).

Ta vẽ được đồ thị như hình dưới:

d) Xét hàm số y = 2x² – 5, ta có:

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = 2x² – 5 là một parabol (P):

– Có đỉnh S với hoành độ x_S = 0, tung độ y_S­ = –5;

– Có trục đối xứng là đường thẳng x = 0 (đường thẳng này chính là trục Oy);

– Bề lõm hướng lên trên vì a > 0;

– Ngoài ra, đồ thị hàm số còn đi qua hai điểm (2; 3) và (–2; 3)

Ta vẽ được đồ thị như hình dưới:

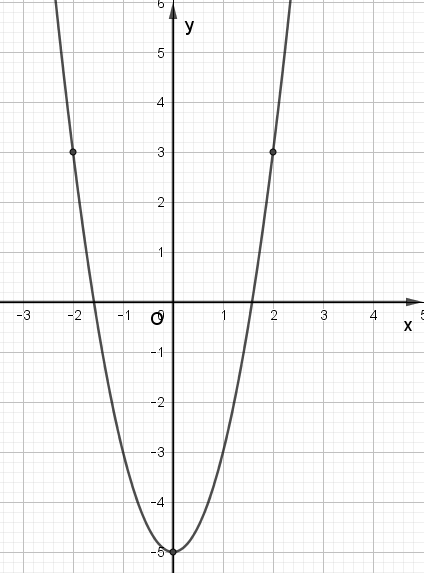
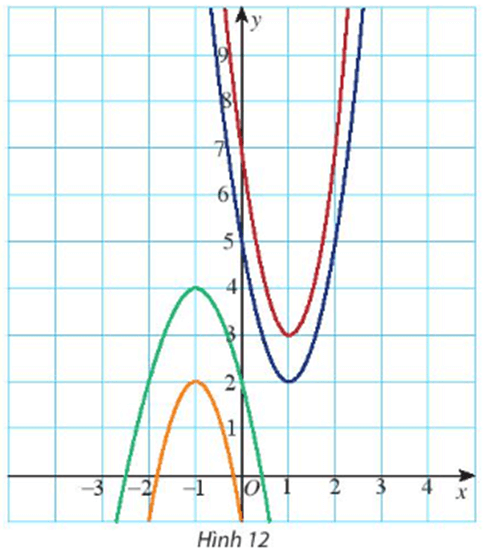
Bài 7 trang 56 Toán lớp 10 Tập 1: Hãy xác định đúng đồ thị của mỗi hàm số sau trên Hình 12.

(P₁): y = - 2x² – 4x + 2;

(P₂): y = 3x² – 6x + 5;

(P₃): y = 4x² – 8x + 7;

(P₄): y = -3x² – 6x + 1.

Lời giải:

(P₁): y = –2x² – 4x + 2 có đồ thị với bề lõm hướng xuống do a = –2 < 0 và cắt trục tung tại điểm (0; 2). Do đó, đồ thị (P₁) là đường parabol màu xanh lá.

(P₂): y = 3x² – 6x + 5 có đồ thị với bề lõm hướng lên do a = 3 > 0 và cắt trục tung tại điểm (0; 5). Do đó, đồ thị (P₂) là đường parabol màu xanh dương.

(P₃): y = 4x² – 8x + 7 có đồ thị với bề lõm hướng lên do a = 4 > 0 và cắt trục tung tại điểm (0; 7). Do đó, đồ thị (P₃) là đường parabol màu đỏ.

(P₄): y = –3x² – 6x – 1 có đồ thị với bề lõm hướng xuống do a = –3 < 0 và cắt trục tung tại điểm (0; –1). Do đó, đồ thị (P₄) là đường parabol màu cam.

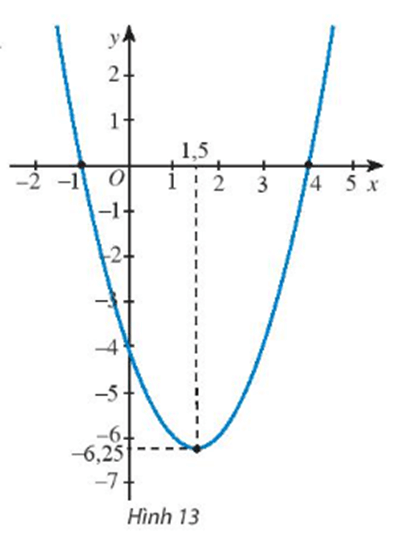
Bài 8 trang 57 Toán lớp 10 Tập 1: Tìm công thức của hàm số bậc hai có đồ thị như Hình 13.

Lời giải:

Gọi hàm số bậc hai có đồ thị như Hình 13 có dạng là y = ax² + bx + c (với a, b, c là các số thực, a ≠ 0).

Đồ thị hàm số cắt trục tung tại điểm (0; –4) nên ta có:

a.0² + b.0 + c = –4 ⇒ c = –4.

Đồ thị hàm số cắt trục hoành tại hai điểm (–1; 0) và (4; 0) nên ta có:

a.(–1)² + b.(–1) – 4 = 0 ⇒ a – b  = 4  (1)

a.4² + b.4 – 4 = 0 ⇒ 16a + 4b = 4 (2)

Từ (1) và (2) ta có hệ phương trình:

$\left\{\begin{array}{l}a-b=4\\ 16a+4b=4\end{array}\right.\iff \left\{\begin{array}{l}a-b=4\\ 20a=20\end{array}\right.\iff \left\{\begin{array}{l}1-b=4\\ a=1\end{array}\right.\iff \left\{\begin{array}{l}b=-3\\ a=1\end{array}\right.$

Vậy hàm số bậc hai cần tìm là y = x² – 3x – 4 .

Bài 9 trang 57 Toán lớp 10 Tập 1: Chiếc cầu dây văng một nhịp được thiết kế hai bên thành cầu có dạng parabol và được cố định bằng các dây cáp song song.

Dựa vào bản vẽ ở Hình 14, hãy tính chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên. Biết:

- Dây dài nhất là 5m, dây ngắn nhất là 0,8m. Khoảng cách giữa các dây bằng nhau.

- Nhịp cầu dài 30m.

- Cần tính thêm 5% chiều dài mỗi sợi dây cáp để neo cố định.

Lời giải:

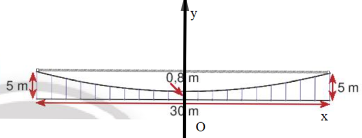
Chọn hệ trục tọa độ như hình vẽ.

Trong đó, khoảng cách giữa các dây bằng nhau và có 20 khoảng cách nên mỗi khoảng cách ứng với 30 : 20 = 1,5 m.

Gọi dạng parabol của thành cầu là đồ thị của hàm số y = ax² + bx + c (a, b, c là các số thực, a ≠ 0).

Đồ thị hàm số cắt trục tung tại điểm (0; 0,8) nên ta có:

a.0² + b.0 + c = 0,8 ⇒ c = 0,8

Tại hai đầu cầu, tức y = 5 thì ta có hai giá trị x thỏa mãn là x₁ = –15 và x₂ = 15

Từ đó ta có:

a.(–15)² + b.(–15) + 0,8 = 5 ⇒ 225a – 15b = 4,2      (1)

a.15² + b.15 + 0,8 = 5 ⇒ 225a + 15b = 4,2              (2)

Từ (1) và (2) ta có hệ phương trình $\left\{\begin{array}{l}225a-15b=4,2\\ 225a+15b=4,2\end{array}\right.\iff \left\{\begin{array}{l}a=\frac{7}{375}\\ b=0\end{array}\right.$ .

Vậy phương trình parabol cần tìm là: $y=\frac{7}{375}{x}^2+0,8$.

Độ dài mỗi dây ở vị trí hoành độ tương ứng là:

Tại x = 0, độ dài dây là: 0,8 + 5%.0,8 = 0,84 (m)

Tại x = 1,5 và x = –1,5 thì độ dài dây là:

$\frac{7}{375}.1,5^2+0,8+5\%.\left(\frac{7}{375}.1,5^2+0,8\right)=0,8841$ (m)

Tại x = 3 và x = –3 thì độ dài dây là:

$\frac{7}{375}{.3}^2+0,8+5\%.\left(\frac{7}{375}{.3}^2+0,8\right)=1,0164$ (m)

Tại x = 4,5 và x = –4,5 thì độ dài dây là:

$\frac{7}{375}.4,5^2+0,8+5\%.\left(\frac{7}{375}.4,5^2+0,8\right)=1,2369$ (m)

Tại x = 6 và x = –6 thì độ dài dây là:

$\frac{7}{375}{.6}^2+0,8+5\%.\left(\frac{7}{375}{.6}^2+0,8\right)=1,5456$ (m)

Tại x = 7,5 và x = –7,5 thì độ dài dây là:

 $\frac{7}{375}.7,5^2+0,8+5\%.\left(\frac{7}{375}.7,5^2+0,8\right)=1,9425$ (m)

Tại x = 9 và x = –9 thì độ dài dây là:

$\frac{7}{375}{.9}^2+0,8+5\%.\left(\frac{7}{375}{.9}^2+0,8\right)=2,4276$ (m)

Tại x = 10,5 và x = –10,5 thì độ dài dây là:

$\frac{7}{375}.10,5^2+0,8+5\%.\left(\frac{7}{375}.10,5^2+0,8\right)=3,0009$(m)

Tại x = 12 và x = –12 thì độ dài dây là:

$\frac{7}{375}{.12}^2+0,8+5\%.\left(\frac{7}{375}{.12}^2+0,8\right)=3,6624$ (m)

Tại x = 13,5 và x = –13,5 thì độ dài dây là:

$\frac{7}{375}.13,5^2+0,8+5\%.\left(\frac{7}{375}.13,5^2+0,8\right)=4,4121$ (m)

Tại x = 15 và x = –15 thì độ dài dây là:

5 + 5%.5 = 5,25 (m)

Chiều dài tổng cộng của các dây cáp dọc ở hai mặt bên của cầu là:

4.(0,84 + 0,8841 + 1,0164 + 1,2369 + 1,5456 + 1,9425 + 2,4276 + 3,0009 + 3,6624 + 4,4121) = 83,874 (m).