Giải Toán 10 (Chân trời sáng tạo) Bài 1: Vẽ đồ thị hàm số bậc hai bằng phần mềm Geogebra
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 10 Bài 1: Vẽ đồ thị hàm số bậc hai bằng phần mềm Geogebra sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài 1. Mời các bạn đón xem:
Giải bài tập Toán 10 Bài 1: Vẽ đồ thị hàm số bậc hai bằng phần mềm Geogebra
Thực hành 1 trang 88 Toán lớp 10 Tập 2: Vẽ đồ thị các hàm bậc hai sau:
a) y = – x2 + 4x – 3;
b) y = x2 + 2;
c) y = x2 + x + 1;
d) y = x2 – 4x + 4.
Lời giải:
a) y = – x2 + 4x – 3;
Bước 1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online.
Bước 2. Các bước thao tác trên Geogebra:
Nhập phương trình bậc hai theo cú pháp y = – x^2 + 4x – 3 vào vùng nhập lệnh như hình dưới đây:
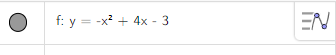
Ta có paraabol hiện trên vùng làm việc như hình vẽ sau:
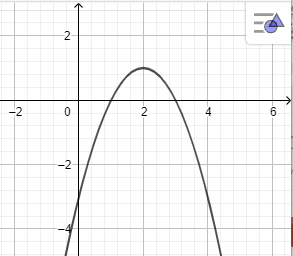
b) y = x2 + 2;
Bước 1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online.
Bước 2. Các bước thao tác trên Geogebra:
Nhập phương trình bậc hai theo cú pháp y = x^2 + 2 vào vùng nhập lệnh như hình dưới đây:
![]()
Ta có paraabol hiện trên vùng làm việc như hình vẽ sau:
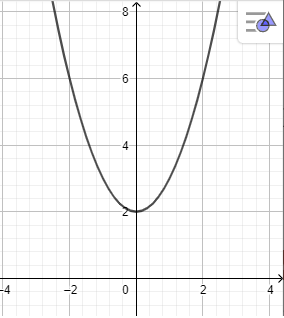
c) y = x2 + x + 1;
Bước 1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online.
Bước 2. Các bước thao tác trên Geogebra:
Nhập phương trình bậc hai theo cú pháp y = 1/2x^2 + x + 1 vào vùng nhập lệnh như hình dưới đây:
![]()
Ta có paraabol hiện trên vùng làm việc như hình vẽ sau:
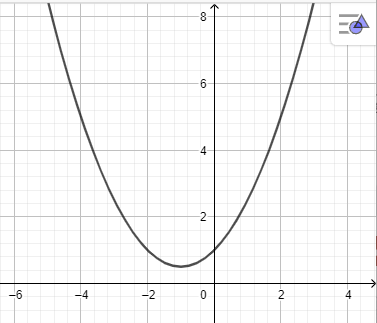
d) y = x2 – 4x + 4.
Bước 1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online.
Bước 2. Các bước thao tác trên Geogebra:
Nhập phương trình bậc hai theo cú pháp y = x^2 – 4x + 4 vào vùng nhập lệnh như hình dưới đây:

Khi đó ta có hình vẽ sau:
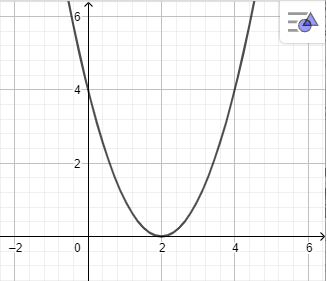
Thực hành 2 trang 89 Toán lớp 10 Tập 2: Điều chỉnh a, b, c để vẽ được nhiều dạng parabol khác nhau:
a) y = x2 – 3x + 2;
b) y = x2;
c) y = –x2;
d) y = 2x2 + 1;
e) y = x2 + 4.
Lời giải:
Bước 1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online.
Bước 2. Các bước thao tác trên Geogebra:
- Tạo các thanh trượt biểu thị các tham số a, b, c bằng cách nhấp chuột liên tiếp vào thanh công cụ ![]() và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.
và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.
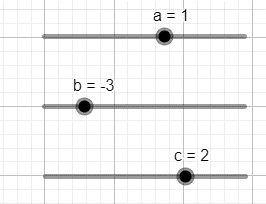
- Nhập công thức hàm số bậc hai y = ax2 + bx + c tại vùng nhập lệnh theo cú pháp: y = ax^2 + bx + c.
- Nhập công thức ∆ = b2 – 4ac bằng cách gõ D = b^2 – 4ac.
a) y = x2 – 3x + 2
- Dùng chuột điều chỉnh các thanh trượt a, b, c để a = 1, b = –3, c = 2 ta được đồ thị trên vùng làm việc như hình vẽ dưới đây:
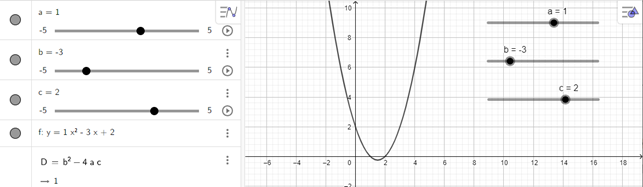
b) y = x2
- Dùng chuột điều chỉnh các thanh trượt a, b, c để a = 1, b = 0, c = 0 ta được đồ thị trên vùng làm việc như hình vẽ dưới đây:
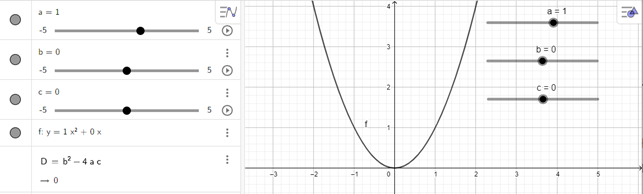
c) y = –x2
- Dùng chuột điều chỉnh các thanh trượt a, b, c để a = –1, b = 0, c = 0 ta được đồ thị trên vùng làm việc như hình vẽ dưới đây:
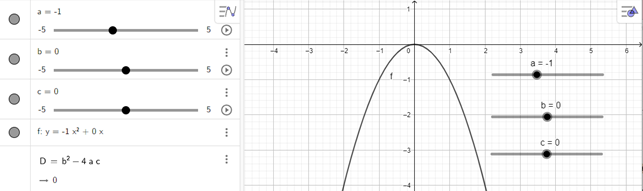
d) y = 2x2 + 1;
- Dùng chuột điều chỉnh các thanh trượt a, b, c để a = 2, b = 0, c = 1 ta được đồ thị trên vùng làm việc như hình vẽ dưới đây:
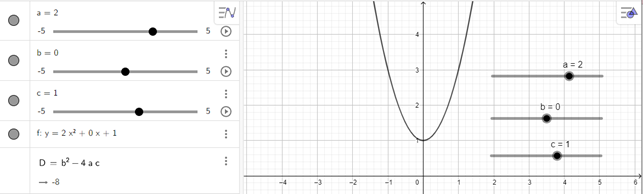
e) y = x2 + 4.
- Dùng chuột điều chỉnh các thanh trượt a, b, c để a = –0,5; b = 0; c = 4 ta được đồ thị trên vùng làm việc như hình vẽ dưới đây:
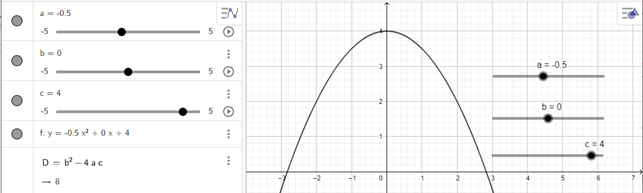
Thực hành 3 trang 90 Toán lớp 10 Tập 2: Hãy tự thiết kế một cổng chào hình parabol.
Lời giải:
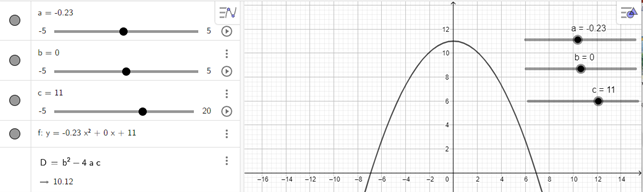
Một cổng chào hình parabol có chiều cao là 7 m và khoảng cách giữa hai chân cổng là 11 m.
– Ta chọn hệ tọa độ để parabol có phương trình y = –ax2 + h.
– Ta có h = 7 m, d = 11 m, suy ra điểm M(5,5; 0) thuộc parabol.
– Thay tọa độ điểm M vào phương trình parabol ta được:
0 = –a.5,52 + 7
– Vậy phương trình parabol là y = –0,23x2 + 11.
– Dùng Geogebra theo cách vẽ đồ thị hàm số bậc hai đã hướng dẫn trong Hoạt động 1, ta vẽ được parabol biểu diễn cổng chào như hình sau: