Cho hàm số bậc hai y = f(x) = ax^2 + bx + c có f(0) = 1, f(1) = 2, f(2) = 5
Lời giải Bài 4 trang 56 Toán 10 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.
Giải Toán lớp 10 Bài 2: Hàm số bậc hai
Bài 4 trang 56 Toán lớp 10 Tập 1: Cho hàm số bậc hai y = f(x) = ax2 + bx + c có f(0) = 1, f(1) = 2, f(2) = 5.
a) Hãy xác định giá trị của các hệ số a, b, c.
b) Xác định tập giá trị và khoảng biến thiên của hàm số.
Lời giải:
a)
Theo đề bài ta có:
f(0) = a.02 + b.0 + c = 1 ⇒ c = 1
f(1) = a.12 + b.1 + c = a + b + 1 = 2 ⇒ a + b = 2 – 1 = 1 (2)
f(2) = a.22 + b.2 + c = 4a + 2b + 1 = 5 ⇒ 4a + 2b = 5 – 1 = 4 (3)
Từ (2) và (3) ta có hệ phương trình:
Vậy a = 1, b = 0, c = 1.
b) Với a = 1, b = 0, c = 1.
Ta có hàm số: y = x2 + 1
Đỉnh S của đồ thị có hoành độ là: và yS = 02 + 1 = 1.
Hay điểm S(0; 1).
Do a = 1 > 0 nên bề lõm của đồ thị hướng lên, ta có bảng biến thiên như sau:
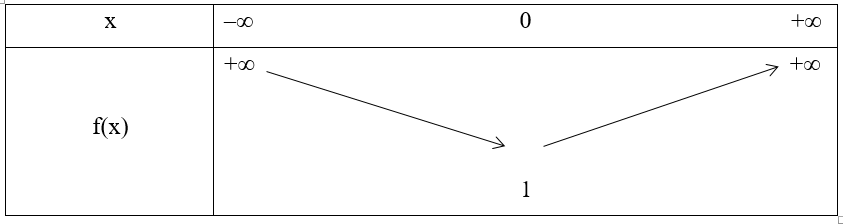
Vậy hàm số đồng biến trên khoảng (0; +∞) và nghịch biến trên khoảng (–∞; 0). Giá trị nhỏ nhất của hàm số là 1 tại x = 0. Tập giá trị của hàm số là T = [1; +∞).


