Xét hàm số: y = f(x) = x^2 – 8x + 19 = (x – 4)^2 + 3 có bảng giá trị
Lời giải Khám phá 2 trang 49 Toán 10 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.
Giải Toán lớp 10 Bài 2: Hàm số bậc hai
Khám phá 2 trang 49 Toán lớp 10 Tập 1: a) Xét hàm số: y = f(x) = x2 – 8x + 19 = (x – 4)2 + 3 có bảng giá trị:
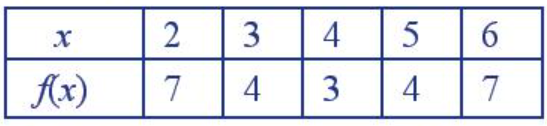
Trên mặt phẳng tọa độ, ta có các điểm (x; f(x)) với x thuộc bảng giá trị đã cho (Hình 1).
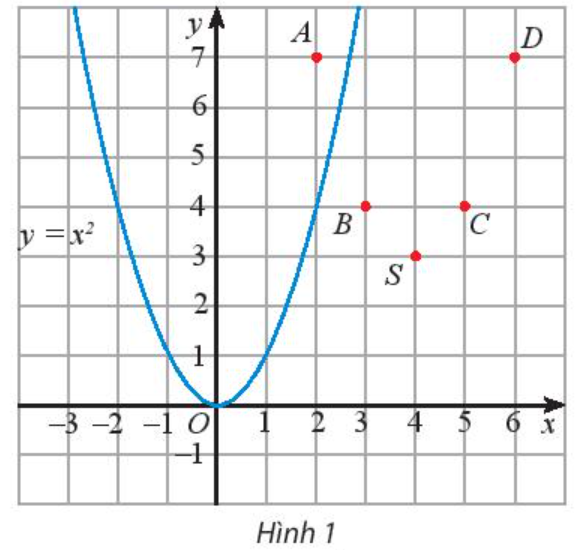Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị của hàm số y = x2 trên Hình 1.
b) Tương tự, xét hàm số: y = g(x) = - x2 + 8x – 13 = - (x – 4)2 + 3 có bảng giá trị:
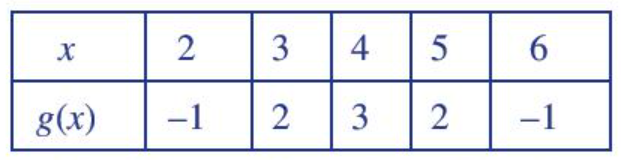
Trên mặt phẳng tọa độ, ta có các điểm (x; g(x)) với x thuộc bảng giá trị đã cho (Hình 2).
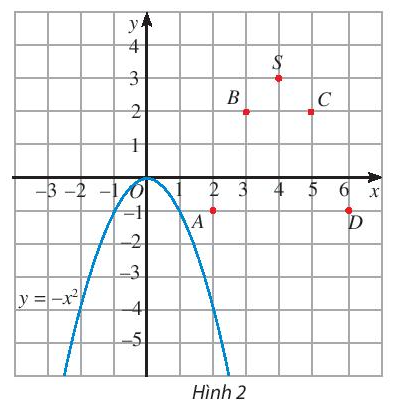
Hãy vẽ đường cong đi qua các điểm A, B, S, C, D và nêu nhận xét về hình dạng của đường cong này so với đồ thị hàm số y = - x2 trên Hình 2.
Lời giải:
a)
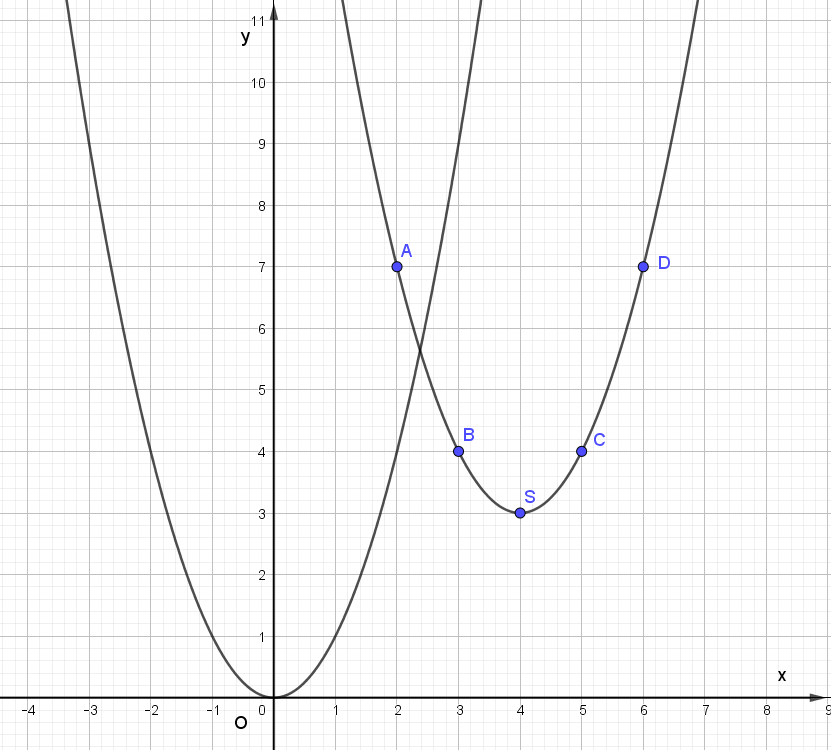
Ta thấy đường cong đi qua các điểm A, B, S, C, D có hình dạng giống với đồ thị của hàm số y = x2 trên Hình 1.
b)
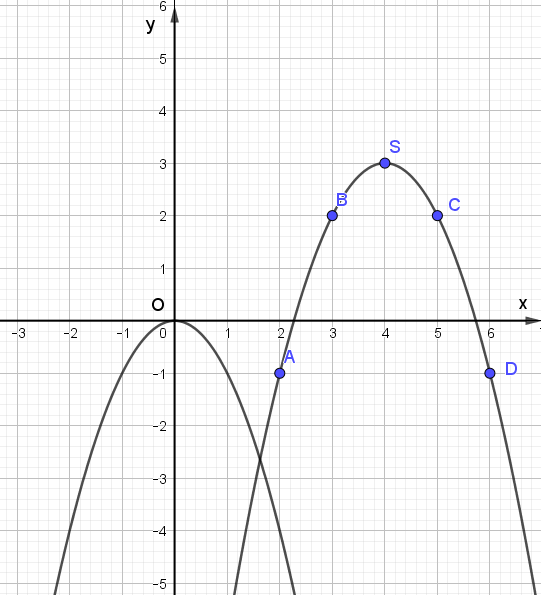
Ta thấy đường cong đi qua các điểm A, B, S, C, D có hình dạng giống với đồ thị của hàm số y = –x2 trên Hình 2.
