Tam giác vuông có hai cạnh bằng nhau được gọi là tam giác vuông cân. Hãy giải thích các khẳng định
Lời giải Bài 4.26 trang 84 Toán 7 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7 Tập 1.
Giải Toán 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Bài 4.26 trang 84 Toán 7 Tập 1: Tam giác vuông có hai cạnh bằng nhau được gọi là tam giác vuông cân.
Hãy giải thích các khẳng định sau:
a) Tam giác vuông cân thì cân tại đỉnh góc vuông;
b) Tam giác vuông cân có hai góc nhọn bằng 45o;
c) Tam giác vuông có một góc nhọn bằng 45o là tam giác vuông cân.
Lời giải:
a)
|
GT |
là tam giác vuông cân;
|
|
KL |
cân tại A. |
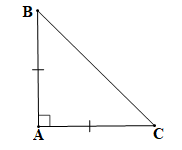
Tam giác ABC vuông tại A nên hai góc nhọn của tam giác phụ nhau suy ra
Khi đó số đo của góc B và góc C sẽ nhỏ hơn 90°.
+) Nếu tam giác ABC cân tại B nên (tính chất tam giác cân).
Mà nên (vô lí vì )
Suy ra tam giác ABC vuông tại A thì không thể cân tại B.
+) Nếu tam giác ABC cân tại C nên (tính chất tam giác cân).
Mà nên (vô lí vì )
Suy ra tam giác ABC vuông tại A thì không thể cân tại C.
Do vậy tam giác ABC vuông tại A và cân tại A.
b)
|
GT |
là tam giác vuông cân. |
|
KL |
Hai góc nhọn bằng 45°. |
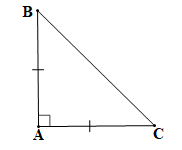
Tam giác ABC vuông cân nên tam giác ABC cân tại đỉnh A (theo câu a).
Suy ra (tính chất tam giác cân).
Mà trong một tam giác vuông, hai góc nhọn phụ nhau nên ta có: .
Do đó
Khi đó
c)
|
GT |
vuông tại A, |
|
KL |
là tam giác vuông cân. |
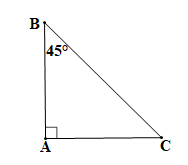
Tam giác ABC vuông tại A (theo giả thiết) nên hai góc nhọn phụ nhau.
Do đó
Suy ra
Khi đó suy ra tam giác ABC cân tại A.
Mà tam giác ABC vuông tại A nên tam giác ABC vuông cân tại A.
Vậy tam giác ABC vuông cân tại A.
Xem thêm lời giải bài tập Toán 7 Tập 1 Kết nối tri thức hay, chi tiết khác:
Mở đầu trang 80 Toán 7 Tập 1: Theo em, trên bản thiết kế làm thế nào để xác định được chính xác điểm C thể hiện đỉnh ngôi nhà
Câu hỏi trang 80 Toán 7 Tập 1: Hãy nêu tên tất cả các tam giác cân trong Hình 4.59. Với mỗi tam giác cân đó, hãy nêu tên cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của chúng
HĐ 1 trang 81 Toán 7 Tập 1: Quan sát tam giác ABC cân tại A như Hình 4.60. Lấy D là trung điểm của đoạn thẳng BC
HĐ 2 trang 81 Toán 7 Tập 1: Cho tam giác MNP có góc M = góc N. Vẽ tia phân giác PK của góc MPN (K ∈ MN )
Luyện tập 1 trang 81 Toán 7 Tập 1: Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62
Thử thách nhỏ trang 81 Toán 7 Tập 1: Một tam giác có gì đặc biệt nếu thỏa mãn một trong các điều kiện sau: a)Tam giác có ba góc bằng nhau
HĐ 3 trang 81 – 82 Toán 7 Tập 1: Đánh dấu hai điểm A và B nằm trên hai mép tờ giấy A4, nối A và B để được đoạn thẳng AB
Câu hỏi trang 82 Toán 7 Tập 1: Trong Hình 4.64, bạn Lan vẽ đường trung trực của các đoạn thẳng. Theo em, hình nào Lan vẽ đúng
HĐ 4 trang 82 Toán 7 Tập 1: Trên mảnh giấy trong Hoạt động 3, lấy điểm M bất kì trên đường thẳng d
Luyện tập 2 trang 83 Toán 7 Tập 1: Cho M là một điểm nằm trên đường trung trực của đoạn thẳng AB. Biết AM = 3 cm và góc MAB = 60 độ (H.4.67)
Thực hành trang 83 Toán 7 Tập 1: Sử dụng thước thẳng và compa để vẽ đường trung trực của đoạn thẳng AB như sau
Bài 4.23 trang 84 Toán 7 Tập 1: Cho tam giác ABC cân tại A và các điểm E, F lần lượt nằm trên các cạnh AC, AB sao cho BE vuông góc với AC
Bài 4.24 trang 84 Toán 7 Tập 1: Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC
Bài 4.25 trang 84 Toán 7 Tập 1: Cho tam giác ABC và M là trung điểm của đoạn thẳng BC. a) Giả sử AM vuông góc với BC. Chứng minh tam giác ABC cân tại A
Bài 4.26 trang 84 Toán 7 Tập 1: Tam giác vuông có hai cạnh bằng nhau được gọi là tam giác vuông cân. Hãy giải thích các khẳng định
Bài 4.27 trang 84 Toán 7 Tập 1: Trong Hình 4.70, đường thẳng nào là đường trung trực của đoạn thẳng AB
Bài 4.28 trang 84 Toán 7 Tập 1: Cho tam giác ABC cân tại A có đường cao AD. Chứng minh rằng đường thẳng AD là đường trung trực của đoạn thẳng BC
Bài viết liên quan
- Giải Toán 7 (Kết nối tri thức) Luyện tập chung trang 74
- Giải Toán 7 (Kết nối tri thức) Bài 15: Các trường hợp bằng nhau của tam giác vuông
- Giải Toán 7 (Kết nối tri thức) Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
- Giải Toán 7 (Kết nối tri thức) Luyện tập chung trang 85, trang 86
- Giải Toán 7 (Kết nối tri thức) Bài tập cuối chương 4 trang 87
