Giải bài tập Toán 7 Bài 12: Tổng các góc trong một tam giác

Video giải bài tập Toán 7 Bài 12: Tổng các góc trong một tam giác

Mở đầu 

Mở đầu trang 60 Toán 7 Tập 1: Người ta có thể xếp các viên gạch hình tam giác giống hệt nhau để trang trí như Hình 4.1. Em có nhận xét gì về ba góc tại mỗi đỉnh chung của ba tam giác? Từ đó em rút ra kết luận gì về vị trí của ba điểm A, B, C?

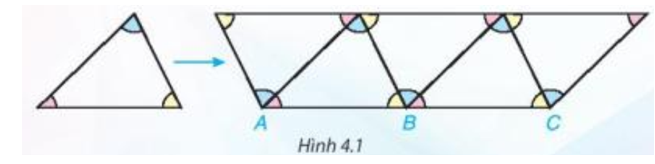
Lời giải:

Nhận xét: Khi xếp các viên gạch hình tam giác giống hệt nhau để trang trí như Hình 4.1 ta thấy ba góc tại mỗi đỉnh chung của ba tam giác (như trên hình vẽ ba góc tại đỉnh B) có tổng số đo bằng 180°.

Kết luận: ba điểm A, B, C thẳng hàng.

Tổng các góc trong một tam giác

HĐ 1 trang 60 Toán 7 Tập 1: Vẽ tam giác MNP bất kì, đo ba góc của tam giác đó.

- Tổng số đo ba góc của tam giác MNP bằng bao nhiêu?

- So sánh kết quả của em với các bạn và rút ra nhận xét.

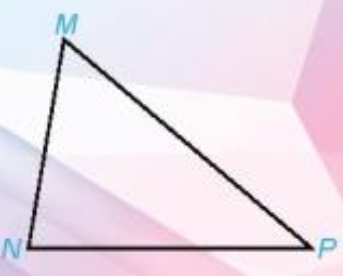
Lời giải:

a) Tổng số đo ba góc của tam giác MNP bằng 180°.

b) Kết quả của em giống kết quả của các bạn khác.

Nhận xét: Tổng số đo ba góc của tam giác bằng 180°.  

HĐ 2 trang 61 Toán 7 Tập 1: Cắt một hình tam giác bằng giấy bất kì (H.4.2a). Đánh dấu ba góc là x, y, z. Cắt hai góc y, z và ghép lên góc x như Hình 4.2b. Từ đó, em hãy dự đoán tổng số đo các góc x, y, z của tam giác ban đầu.

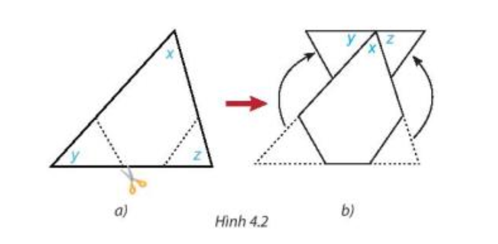
Lời giải:

Sau khi cắt ghép ta được Hình 4.2b, tại điểm chung gốc của 3 góc x, y, z có tổng số đo ba góc bằng 180° nên ta dự đoán tổng số đo các góc x, y, z của tam giác ban đầu bằng 180°.  

Câu hỏi trang 61 Toán 7 Tập 1: Trở lại tình huống mở đầu, tổng ba góc tại mỗi đỉnh chung của ba tam giác (chẳng hạn tại B trong Hình 4.1) bằng bao nhiêu độ? Ba điểm A, B, C có thẳng hàng không?

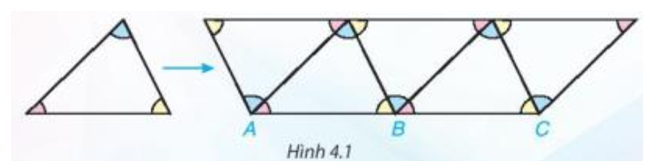
Lời giải:

Trong hình vẽ trên, tổng số đo ba góc tại đỉnh chung B của ba tam giác bằng 180°.

Khi đó ba điểm A, B, C thẳng hàng. 

Luyện tập trang 62 Toán 7 Tập 1: Cho tam giác ABC vuông tại A. Tính tổng hai góc B và C.

Lời giải:

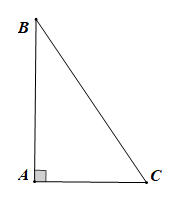
Chứng minh (Hình vẽ trên):

Theo giả thiết tam giác ABC vuông tại A nên $\widehat{A}=90°.$ 

Trong tam giác ABC ta có $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (Định lí tổng ba góc trong một tam giác).

Suy ra $\widehat{B}+\widehat{C}=180°-\widehat{A}=180°-90°=90°.$ 

Vậy $\widehat{B}+\widehat{C}=90°.$  

Vận dụng trang 62 Toán 7 Tập 1: Cho tam giác ABC và Cx là tia đối của tia CB (H.4.5).

Chứng minh rằng $\widehat{ACx}=\widehat{BAC}+\widehat{CBA}.$

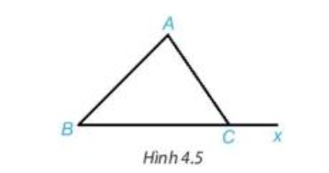
Lời giải:

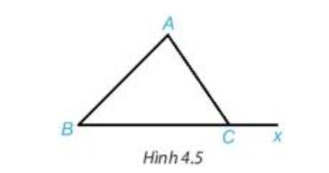
Chứng minh (Hình vẽ trên):

Theo giả thiết Cx là tia đối của tia CB nên hai góc ACB và Acx là hai góc kề bù, hay $\widehat{ACB}+\widehat{ACx}=180°$ (tính chất hai góc kề bù).

Suy ra $\widehat{ACx}=180°-\widehat{ACB}$ (1).

Trong tam giác ABC ta có $\widehat{BAC}+\widehat{ACB}+\widehat{CBA}=180°$ (Định lí tổng ba góc trong một tam giác).

Suy ra $\widehat{BAC}+\widehat{CBA}=180°-\widehat{ACB}$ (2).

Từ (1) và (2) ta có $\widehat{ACx}=\widehat{BAC}+\widehat{CBA}\left(=180°-\widehat{ACB}\right)$.

Vậy $\widehat{ACx}=\widehat{BAC}+\widehat{CBA}.$ 

Bài tập

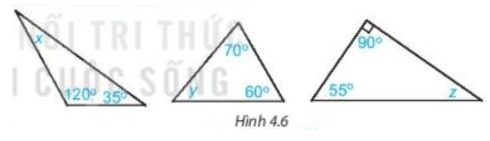
Bài 4.1 trang 62 Toán 7 Tập 1: Tính số đo các góc x, y, z trong Hình 4.6.

Lời giải:

+)

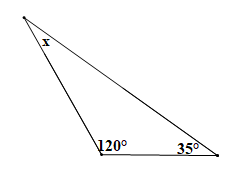
Áp dụng định lí tổng ba góc trong một tam giác cho tam giác trên hình vẽ ta có:

x + 120° + 35° = 180° suy ra x = 180° – 120° – 35° = 25°.

Vậy x = 25°.

+)

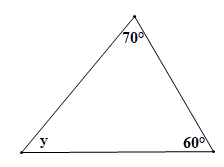
Áp dụng định lí tổng ba góc trong một tam giác cho tam giác trên hình vẽ ta có:

y + 60° + 70° = 180° suy ra y = 180° – 60° – 70° = 50°.

Vậy y = 50°.

+)

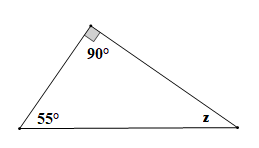
Tam giác trong hình vẽ là tam giác có một góc có số đo bằng 90° nên là tam giác vuông, do đó hai góc nhọn phụ nhau.

Suy ra z + 55° = 90°

z = 90° – 55°

z = 35°.

Vậy z = 35°. 

Bài 4.2 trang 62 Toán 7 Tập 1: Trong các tam giác (H.4.7), tam giác nào là tam giác nhọn, tam giác vuông, tam giác tù?

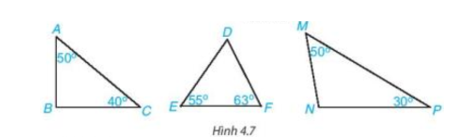
Lời giải:

+)

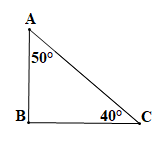
Trên hình vẽ, tam giác ABC có $\widehat{A}=50°,\widehat{C}=40°,$ áp dụng định lí tổng ba góc trong một tam giác ta có $\widehat{A}+\widehat{B}+\widehat{C}=180°$.

Suy ra $\widehat{B}=180°-\widehat{A}-\widehat{C}$

$\widehat{B}=180°-50°-40°$ 

$\widehat{B}=90°$

Ta thấy trong tam giác ABC có $\widehat{B}=90°$ là một góc vuông nên tam giác ABC là tam giác vuông tại B.

Vậy tam giác ABC là tam giác vuông tại B.

+)

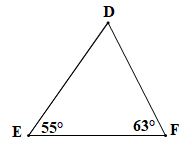
Trên hình vẽ, tam giác DEF có $\widehat{E}=55°,\widehat{F}=63°,$ áp dụng định lí tổng ba góc trong một tam giác ta có $\widehat{D}+\widehat{E}+\widehat{F}=180°$.

Suy ra $\widehat{D}=180°-\widehat{E}-\widehat{F}$

$\widehat{D}=180°-55°-63°$ 

$\widehat{D}=62°$

Ta thấy trong tam giác DEF có $\widehat{D}=62°,\widehat{E}=55°,\widehat{F}=63°$ là ba góc nhọn nên tam giác DEF là tam giác nhọn.

Vậy tam giác DEF là tam giác nhọn.

+)

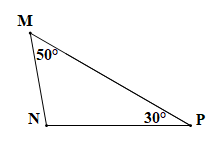
Trên hình vẽ, tam giác MNP có $\widehat{M}=50°,\widehat{P}=30°,$ áp dụng định lí tổng ba góc trong một tam giác ta có $\widehat{M}+\widehat{N}+\widehat{P}=180°$.

Suy ra $\widehat{N}=180°-\widehat{M}-\widehat{P}$

$\widehat{N}=180°-50°-30°$ 

$\widehat{N}=100°$

Ta thấy trong tam giác MNP có $\widehat{N}=100°$ là một góc tù nên tam giác MNP là tam giác tù.

Vậy tam giác MNP là tam giác tù. 

Bài 4.3 trang 62 Toán 7 Tập 1: Tính các số đo x, y, z trong Hình 4.8.

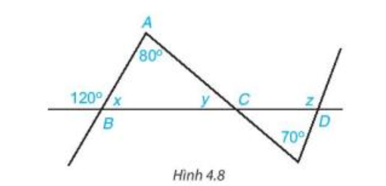
Lời giải:

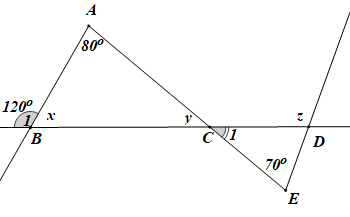
+) Trên hình vẽ ta thấy góc B₁ và góc ABC là hai góc kề bù nên $\widehat{B_1}+\widehat{ABC}=180°$ (tính chất hai góc kề bù).

Suy ra $\widehat{ABC}=180°-\widehat{B_1}$ 

Hay $x=\widehat{ABC} =180°–120°=60°.$ 

+) Xét tam giác ABC có $\widehat{ABC}=60°,\widehat{CAB}=80°,$ áp dụng định lí tổng ba góc trong một tam giác ta có $\widehat{ABC}+\widehat{BCA}+\widehat{CAB}=180°$ 

Suy ra $\widehat{BCA}=180°-\widehat{CAB}-\widehat{ABC}$

Hay  $y=\widehat{BCA}=180°–80°–60° =40°.$ 

+) Góc C₁ và góc $\widehat{ACB}$ là hai góc đối đỉnh nên $\widehat{C_1}=\widehat{ACB}=y$ (tính chất hai góc đối đỉnh).

Mà y = 40°.

Do đó $\widehat{C_1}=40°.$ 

+) Xét tam giác CDE có góc z là góc ngoài của tam giác tại đỉnh D, do đó $z=\widehat{C_1}+\widehat{E}$ (tính chất góc ngoài của một tam giác).

Suy ra z = 40° +  70° = 110°.

Vậy x = 60°, y = 40° và z = 110°.