Giải bài tập Toán 7 Luyện tập chung trang 35 

Bài 7.18 trang 35 Toán 7 Tập 2:

Cho các đơn thức: 2x⁶; -5x³; -3x⁵; x³; $\frac{3}{5}$x²; $-\frac{1}{2}$x²; 8; -3x. Gọi A là tổng của các đơn thức đã cho.

a) Hãy thu gọn tổng A và sắp xếp các hạng tử để được một đa thức.

b) Tìm hệ số cao nhất, hệ số tự do và hệ số của x² của đa thức thu được.

Lời giải:

a) A = 2x⁶ + (-5x³) + (-3x⁵) + x³ + $\frac{3}{5}$x² + ($-\frac{1}{2}$x²) + 8 + (-3x)

        = 2x⁶ - 3x⁵ + (-5x³ + x³) + $\left(\frac{3}{5}{x}^2-\frac{1}{2}{x}^2\right)$ - 3x + 8

        = 2x⁶ - 3x⁵ + (-4x³) + $\left(\frac{6}{10}{x}^2-\frac{5}{10}{x}^2\right)$ - 3x + 8

        = 2x⁶ - 3x⁵ - 4x³ + $\frac{1}{10}$x² - 3x + 8.

Vậy A = 2x⁶ - 3x⁵ - 4x³ + $\frac{1}{10}$x² - 3x + 8.

b) Trong đa thức A, hạng tử có bậc cao nhất là 2x⁶ nên hệ số cao nhất của đa thức A là 2.

Hạng tử có bậc bằng 0 là 8 nên hệ số tự do của đa thức A là 0.

Hệ số của x² của đa thức A là $\frac{1}{10}$.

Bài 7.19 trang 35 Toán 7 Tập 2:

Một bể chứa nước có dạng hình hộp chữ nhật được thiết kế với kích thước theo tỉ lệ:

Chiều cao : chiều rộng : chiều dài = 1 : 2 : 3.

Trong bể hiện còn 0,7 m³ nước. Gọi chiều cao của bể là x (mét).

Hãy viết đa thức biểu thị số mét khối nước cần phải bơm thêm vào bể để bể đầy nước. Xác định bậc của đa thức đó.

Lời giải:

Do chiều cao : chiều rộng : chiều dài = 1 : 2 : 3 nên chiều rộng bằng 2 lần chiều cao và chiều dài bằng 3 lần chiều cao.

Khi chiều cao của bể là x (m) thì chiều rộng của bể là 2x (m), chiều dài của bể là 3x (m).

Thể tích của bể là:

 x . 2x . 3x = 2 . 3 . x . x . x = 6x³ (m³).

Do trong bể có 0,7 m³ nước nên số nước cần phải bơm thêm để bể đầy bước là:

6x³ - 0,7 (m³).

Vậy đa thức biểu thị số mét khối nước cần phải bơm thêm vào bể để bể đầy nước là 6x³ - 0,7 (m³).

Đa thức trên có hạng tử có bậc cao nhất là 6x³ nên bậc của đa thức trên bằng 3.

Bài 7.20 trang 35 Toán 7 Tập 2:

Ngoài thang nhiệt độ Celsius (độ C), nhiều nước còn dùng thang nhiệt độ Fahrenheit, gọi là độ F để đo nhiệt độ trong dự báo thời tiết. Muốn tính xem x °C tương ứng với bao nhiêu độ F, ta dùng công thức:

T(x) = 1,8x + 32.

Chẳng hạn, 0°C tương ứng với T(0) = 32 (°F).

a) Hỏi 0°F tương ứng với bao nhiêu độ C?

b) Nhiệt độ vào một ngày mùa hè ở Hà Nội là 35 °C. Nhiệt độ đó tương ứng với bao nhiêu độ F?

c) Nhiệt độ vào một ngày mùa đông ở New York (Mỹ) là 41 °F. Nhiệt độ đó tương ứng với bao nhiêu độ C?

Lời giải:

a) Ta có T(x) = 0 (°F)

Do đó 1,8x + 32 = 0

1,8x = -32

x = -32 : 1,8

x = $\frac{-320}{18}$ ≈ -17,8.

Vậy 0°F tương ứng với khoảng -17,8 °C.

b) Ta có T(35) = 1,8 . 35 + 32 = 63 + 32 = 95.

Do đó 35°C tương ứng với 95°F.

c) Ta có T(x) = 41

Do đó 1,8x + 32 = 41

1,8x = 41 - 32

1,8x = 9

x = 9 : 1,8

x = 5.

Vậy 41°F tương ứng với 5°C.

Bài 7.21 trang 35 Toán 7 Tập 2:

Cho hai đa thức P = -5x⁴ + 3x³ + 7x² + x - 3 và Q = 5x⁴ - 4x³ - x² + 3x + 3.

a) Xác định bậc của mỗi đa thức P + Q và P - Q.

b) Tính giá trị của mỗi đa thức P + Q và P - Q tại x = 1; x = -1.

c) Đa thức nào trong hai đa thức P + Q và P - Q có nghiệm là x = 0?

Lời giải:

a) Đặt tính cộng P + Q như sau:

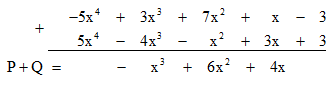
Do đó P + Q = – x³ + 6x² + 4x. Đa thức này có hạng tử bậc cao nhất là – x³ nên bậc của đa thức P + Q là 3.

Đặt tính trừ P – Q như sau:

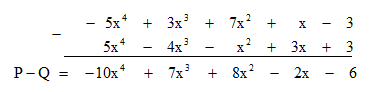
Do đó P – Q = –10x⁴ + 7x³ + 8x² – 2x – 6. Đa thức này có hạng tử bậc cao nhất là -10x⁴ nên bậc của đa thức P – Q là 4.

b) Thay x = 1 vào đa thức P + Q ta có:

P + Q = -1³ + 6 . 1² + 4 . 1 = -1 + 6 + 4 = 9.

Thay x = -1 vào đa thức P + Q ta có:

P + Q = -(-1)³ + 6 . (-1)² + 4 . (-1) = -(-1) + 6 . 1 - 4 = 1 + 6 - 4 = 3.

Thay x = 1 vào đa thức P - Q ta có:

P - Q = -10 . 1⁴ + 7 . 1³ + 8 . 1² - 2 . 1 - 6 = -10 + 7 + 8 - 2 - 6 = -3.

Thay x = -1 vào đa thức P - Q ta có:

P - Q = -10 . (-1)⁴ + 7 . (-1)³ + 8 . (-1)² - 2 . (-1) - 6

          = - 10 . 1 + 7 . (-1) + 8 . 1 + 2 - 6

          = - 10 - 7 + 8 + 2 - 6

          = - 13.

c) Ta thấy đa thức P + Q = – x³ + 6x² + 4x có hệ số tự do bằng 0 nên đa thức P + Q có nghiệm x = 0.

Thay x = 0 vào đa thức P - Q ta có:

P - Q = -10 . 0⁴ + 7 . 0³ + 8 . 0² - 2 . 0 - 6 = -6.

Do đó x = 0 không là nghiệm của đa thức P – Q.

Vậy x = 0 là nghiệm của đa thức P + Q.

Bài 7.22 trang 35 Toán 7 Tập 2:

Một xe khách đi từ Hà Nội lên Yên Bái (trên đường cao tốc Hà Nội - Lào Cai) với vận tốc 60 km/h. Sau đó 25 phút, một xe du lịch cũng đi từ Hà Nội lên Yên Bái (đi cùng đường với xe khách) với vận tốc 85 km/h. Cả hai xe đều không nghỉ dọc đường.

a) Gọi D(x) là đa thức biểu thị quãng đường xe du lịch đi được và K(x) là đa thức biểu thị quãng đường xe khách đi được kể từ khi xuất phát cho đến khi xe du lịch đi được x giờ. Tìm D(x) và K(x).

b) Chứng tỏ rằng đa thức f(x) = K(x) - D(x) có nghiệm x = 1. Hãy giải thích ý nghĩa nghiệm x = 1 của đa thức f(x).

Lời giải:

a) Đổi 25 phút = $\frac{5}{12}$ giờ.

Do xe du lịch đi sau xe khách 25 phút nên khi xe du lịch đi được x giờ thì xe khách đi được x + $\frac{5}{12}$ giờ.

Quãng đường xe du lịch đi được trong x giờ là: 85x (km).

Quãng đường xe khách đi được trong x + $\frac{5}{12}$ giờ là:

60$\left(x+\frac{5}{12}\right)$ = 60x + 60 . $\frac{5}{12}$ = 60x + 25 (km).

Vậy D(x) = 85x (km) và K(x) = 60x + 25 (km).

b) Ta có:

f(x) = K(x) - D(x) = 60x + 25 - 85x = 25 + (60x - 85x) = 25 - 25x.

Thay x = 1 vào đa thức f(x) ta được f(1) = 25 - 25 . 1 = 25 – 25 = 0.

Do đó x = 1 là nghiệm của đa thức f(x).

D(x) là đa thức biểu thị quãng đường xe du lịch đi được và K(x) là đa thức biểu thị quãng đường xe khách đi được kể từ khi xuất phát cho đến khi xe du lịch đi được x giờ nên

f(x) =  K(x) - D(x) là khoảng cách giữa hai xe tại thời điểm xe xu lịch đi được x giờ.

Khi x = 1 thì f(x) = 0 tức khoảng cách giữa hai xe bằng 0.

Do đó lúc này hai xe gặp nhau, xe du lịch đuổi kịp xe khách.

Vậy sau 1 giờ kể từ khi xe du lịch xuất phát thì xe du lịch đuổi kịp xe khách.