Giải bài tập Toán 7 Bài tập cuối chương 4 trang 87 

Bài 4.33 trang 87 Toán 7 Tập 1: Tính các số đo x, y trong các tam giác dưới đây (H.4.75).

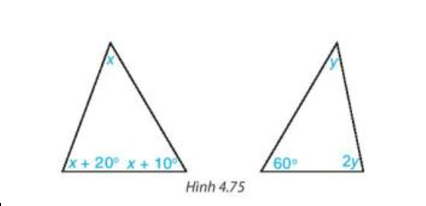
Lời giải: 

+)

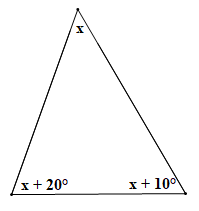
Áp dụng định lí tổng ba góc trong tam giác ta có: x + (x + 10°) + (x + 20°) = 180°.

Suy ra x + x + 10° + x + 20° = 180°.

3.x + 30° = 180°.

3.x = 180° – 30°

3.x = 150°

x = 50°

Vậy x = 50°.

+)

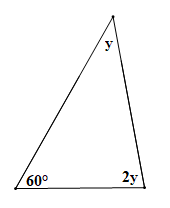
Áp dụng định lí tổng ba góc trong tam giác ta có: y + 2y + 60° = 180°.

Suy ra 3.y + 60° = 180°

3.y = 120°

y = 40°

Vậy y = 40°. 

Bài 4.34 trang 87 Toán 7 Tập 1: Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng $\widehat{MAN}=\widehat{MBN}.$

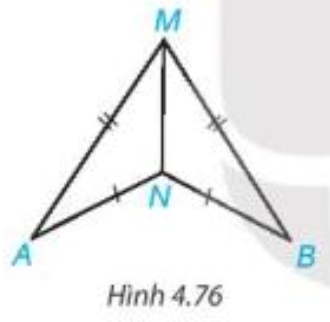
Lời giải: 

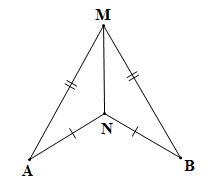
Xét tam giác AMN và tam giác BMN có:

AM = BM (theo giả thiết);

MN là cạnh chung;

AN = BN (theo giả thiết).

Vậy $\Delta AMN=\Delta BMN$ (c.c.c).

Suy ra $\widehat{MAN}=\widehat{MBN}$ (hai góc tương ứng). 

Bài 4.35 trang 87 Toán 7 Tập 1: Trong Hình 4.77, có AO = BO, $\widehat{OAM}=\widehat{OBN}.$ Chứng minh rằng AM = BN.

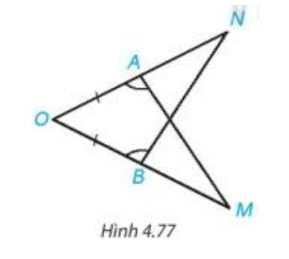
Lời giải: 

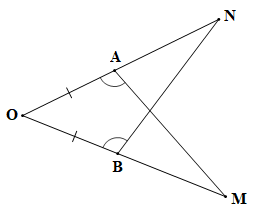
Xét tam giác OAM và tam giác OBN có:

$\widehat{OAM}=\widehat{OBN}$ (theo giả thiết);

OA = OB (theo giả thiết);

$\widehat{MON}$ là góc chung.

Vậy $\Delta OAM=\Delta OBN$ (g.c.g).

Suy ra AM = BN (hai cạnh tương ứng). 

Bài 4.36 trang 87 Toán 7 Tập 1: Trong Hình 4.78, ta có AN = BM, $\widehat{BAN}=\widehat{ABM}.$ Chứng minh rằng $\widehat{BAM}=\widehat{ABN}.$

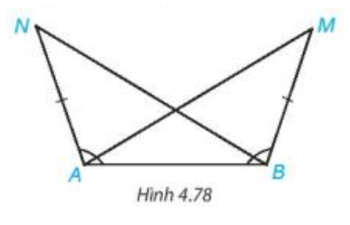
Lời giải: 

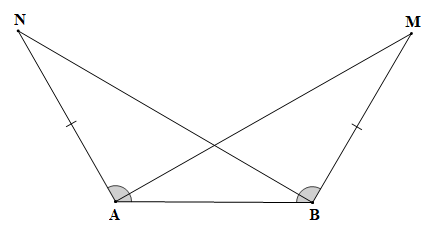
Xét tam giác ABN và tam giác BAM có:

AN = BM (theo giả thiết);

$\widehat{BAN}=\widehat{ABM}$ (theo giả thiết);

AB là cạnh chung.

Vậy $\Delta ABN=\Delta BAM$ (c.g.c).

Suy ra $\widehat{ABN}=\widehat{BAM}$ (hai góc tương ứng).

Bài 4.37 trang 87 Toán 7 Tập 1: Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Chứng minh rằng MB = NB và góc AMB bằng góc ANB.

Lời giải: 

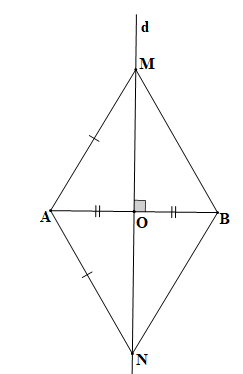
M và N là hai điểm phân biệt nằm trên đường trung trực của AB với AM = AN nên M và N có vị trí như hình vẽ trên.

Gọi O là giao điểm của AB và MN, d là đường trung trực của AB nên $d\perp AB$ tại trung điểm O của AB.

Xét tam giác OAM (vuông tại O) và tam giác OAN (vuông tại O) có:

OA là cạnh chung;

AM = AN (theo giả thiết).

Vậy $\Delta OAM=\Delta OAN$ (cạnh huyền – cạnh góc vuông).

Suy ra OM = ON (hai cạnh tương ứng) và $\widehat{AMO}=\widehat{ANO}$ (hai góc tương ứng).

Xét tam giác OBM (vuông tại O) và tam giác OBN (vuông tại O) có:

OB là cạnh chung;

OM = ON (chứng minh trên).

Vậy $\Delta OBM=\Delta OBN$ (hai cạnh góc vuông).

Suy ra MB = NB (hai cạnh tương ứng) và $\widehat{BMO}=\widehat{BNO}$ (hai góc tương ứng).

Ta có $\widehat{AMO}=\widehat{ANO}$ (chứng minh trên) và $\widehat{BMO}=\widehat{BNO}$ (chứng minh trên) nên $\widehat{AMO}+\widehat{BMO}=\widehat{ANO}+\widehat{BNO}.$

Mà $\widehat{AMB}=\widehat{AMO}+\widehat{BMO}$ và $\widehat{ANB}=\widehat{ANO}+\widehat{BNO}.$

Suy ra $\widehat{AMB}=\widehat{ANB}.$ 

Bài 4.38 trang 87 Toán 7 Tập 1: Cho tam giác ABC cân tại A có $\widehat{A}=120°.$ Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:

a) $\Delta BAM=\Delta CAN;$

b) Các tam giác ANB, AMC lần lượt cân tại N, M.

Lời giải: 

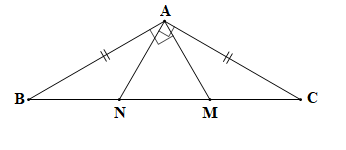
a) Tam giác ABC cân tại A (theo giả thiết) nên AB = AC và $\widehat{B}=\widehat{C}$.

$MA\perp AB$ tại A (theo giả thiết) nên $\widehat{BAM}=90°;$ $NA\perp AC$ tại A (theo giả thiết) nên $\widehat{NAC}=90°;$

Xét tam giác BAM (vuông tại A) và tam giác CAN (vuông tại A) có:

AB = AC (chứng minh trên);

$\widehat{B}=\widehat{C}$ (chứng minh trên).

Vậy $\Delta BAM=\Delta CAN$ (cạnh góc vuông – góc nhọn kề).

b) Trong tam giác ABC có $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng ba góc trong một tam giác).

Suy ra $\widehat{B}+\widehat{C}=180°-\widehat{A}$.

Mà $\widehat{A}=120°$ (theo giả thiết) và $\widehat{B}=\widehat{C}$ (chứng minh trên).

Do đó $\widehat{B}+\widehat{B}=180°-120°$

$2\widehat{B}=60°$ 

$\widehat{B}=30°$ 

Khi đó $\widehat{B}=\widehat{C}=30°.$        (1)

Ta có: $\widehat{BAM}<\widehat{BAC}$ (do 90° < 120°) nên tia AM nằm giữa hai tia AB và AC.

Do đó $\widehat{BAC}=\widehat{BAM}+\widehat{MAC}$.

Suy ra $\widehat{MAC}=\widehat{BAC}-\widehat{BAM}=120°-90°=30°$.   

Vậy $\widehat{MAC}=30°.$            (2)

Tương tự ta cũng có $\widehat{BAC}=\widehat{BAN}+\widehat{NAC}$.

Suy ra $\widehat{BAN}=\widehat{BAC}-\widehat{NAC}=120°-90°=30°.$ 

Vậy $\widehat{BAN}=30°$.            (3)

Từ (1), (2) và (3) ta có: $\widehat{B}=\widehat{C}=\widehat{MAC}=\widehat{BAN}\left(=30°\right).$

Do đó tam giác ABN cân tại N (do $\widehat{B}=\widehat{BAN}$);

Và tam giác ACM cân tại M (do $\widehat{C}=\widehat{MAC}$). 

Bài 4.39 trang 87 Toán 7 Tập 1: Cho tam giác ABC vuông tại A có $\widehat{B}=60°.$ Trên cạnh BC lấy điểm M sao cho $\widehat{CAM}=30°.$ Chứng minh rằng:

a) Tam giác CAM cân tại M;

b) Tam giác BAM là tam giác đều;

c) M là trung điểm của đoạn thẳng BC.

Lời giải: 

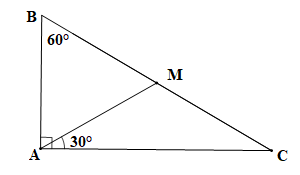
a) Tam giác ABC vuông tại A (theo giả thiết) nên hai góc nhọn phụ nhau, do đó $\widehat{B}+\widehat{C}=90°.$

Suy ra $\widehat{C}=90°-\widehat{B}$ 

Mà  $\widehat{B}=60°$ nên $\widehat{C}=90°-60°=30°$ 

Xét tam giác CAM có $\widehat{CAM}=\widehat{C}=30°$ nên tam giác CAM là tam giác cân tại M.

b) Ta có $\widehat{CAM}<\widehat{CAB}$ (do 30° < 90°) nên tia AM nằm giữa hai tia AB và AC.

Khi đó $\widehat{CAB}=\widehat{CAM}+\widehat{MAB}$.

Suy ra $\widehat{MAB}=\widehat{CAB}-\widehat{CAM}=90°-30°=60°$.

Áp dụng định lí tổng ba góc trong tam giác cho tam giác BAM có: $\widehat{MAB}+\widehat{B}+\widehat{AMB}=180°$.

Suy ra $\widehat{AMB}=180°-\widehat{B}-\widehat{MAB}.$ 

$\widehat{AMB}=180°-60°-60°=60°.$

Khi đó $\widehat{AMB}=\widehat{B}=\widehat{MAB}=60°$.

Suy ra tam giác BAM là tam giác đều.

c) Tam giác AMC cân tại M (chứng minh câu a) nên MA = MC (định nghĩa tam giác cân).

Tam giác BAM là tam giác đều (chứng minh câu b) nên MA = MB (định nghĩa tam giác đều).

Suy ra MB = MC (= MA).

Mà M nằm trên cạnh BC (theo giả thiết)

Do đó M là trung điểm của BC.