Giải Toán 7 (Kết nối tri thức) Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 7 Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài 13. Mời các bạn đón xem:
Giải bài tập Toán 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Video giải bài tập Toán 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Lời giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Hai tam giác ABC và bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau, nghĩa là:
Khi đó ta viết
Vậy để kiểm tra xem hai tam giác có bằng nhau không ta sẽ kiểm tra các cạnh tương ứng và các góc tương ứng của hai tam giác đó có bằng nhau hay không.
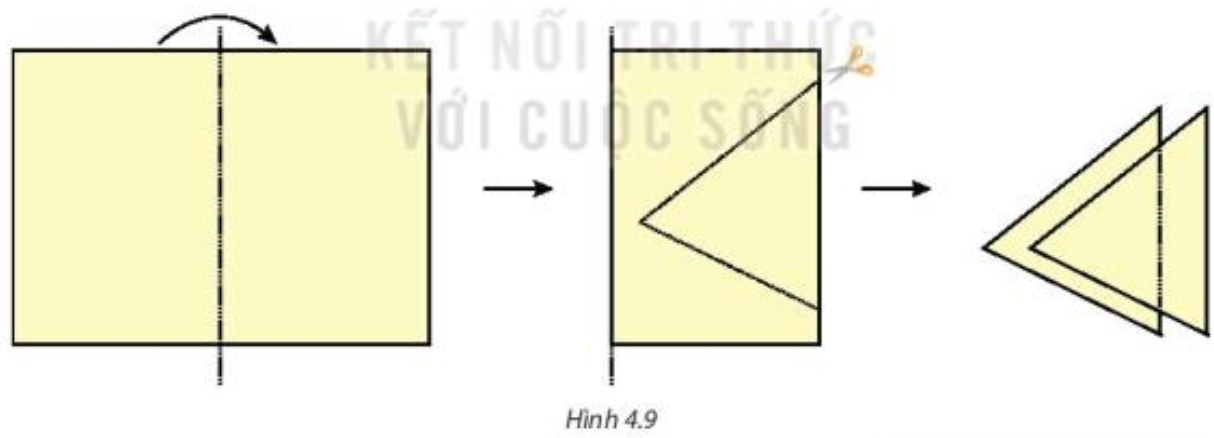
HĐ 1 trang 62 Toán 7 Tập 1: Gấp đôi một tờ giấy rồi cắt như Hình 4.9.
Phần được cắt ra là hai tam giác “chồng khít” lên nhau.
- Các cạnh tương ứng có bằng nhau không?
- Các góc tương ứng có bằng nhau không?
Lời giải:
Sau khi cắt ghép ta thấy:
- Các cạnh tương ứng của hai tam giác có độ dài bằng nhau nên bằng nhau.
- Các góc tương ứng của hai tam giác có số đo bằng nhau nên bằng nhau.
Lời giải:
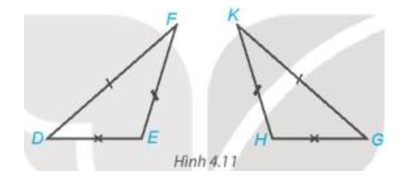
Hai tam giác DEF và GHK (Hình 4.11) bằng nhau nên ta có:
- Các cặp cạnh tương ứng bằng nhau: DE = GH, EF = HK, DF = GK.
- Các cặp góc tương ứng bằng nhau:
Khi đó ta viết
Lời giải:
|
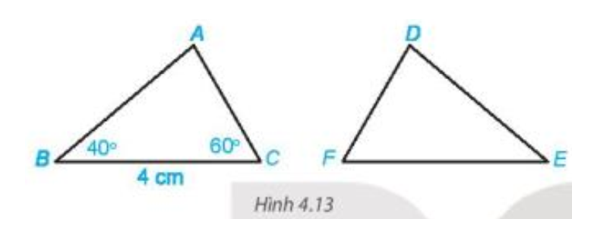
GT |
; BC = 4 cm, |
|
KL |
Tính EF và số đo góc EDF. |
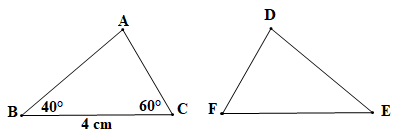
Chứng minh (Hình vẽ trên):
Xét tam giác ABC có áp dụng định lí tổng ba góc trong một tam giác ta có
Suy ra
Vậy
Theo giả thiết ta có
Suy ra BC = EF (hai cạnh tương ứng) và (hai góc tương ứng).
Mà BC = 4 cm (theo giả thiết) và (chứng minh trên).
Do đó EF = 4 cm,
Vậy EF = 4 cm,
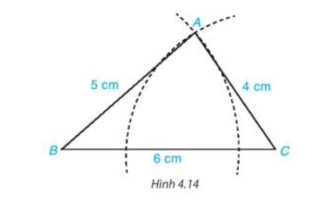
HĐ 2 trang 65 Toán 7 Tập 1: Vẽ tam giác ABC có AB = 5 cm, AC = 4 cm, BC = 6 cm theo các bước sau:
- Dùng thước thẳng có vạch chia vẽ đoạn thẳng BC = 6 cm.
- Vẽ các đoạn thẳng AB, AC ta được tam giác ABC.
Lời giải:
Bước 1. Dùng thước thẳng có vạch chia vẽ đoạn thẳng BC = 6 cm ta được hình vẽ sau:
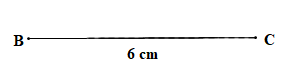
Bước 2. Vẽ cung tròn tâm B bán kính 5 cm và cung tròn tâm C bán kính 4 cm sao cho hai cung tròn cắt nhau tại điểm A, ta được hình vẽ như sau:
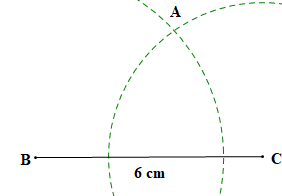
Bước 3. Vẽ các đoạn thẳng AB, AC ta được tam giác ABC như hình vẽ sau:
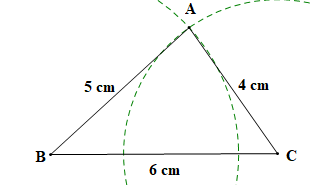
- Hai tam giác ABC và A'B'C' có bằng nhau không?
Lời giải:
Vẽ tam giác A'B'C' tương tự như tam giác ABC ta được hình vẽ dưới đây.
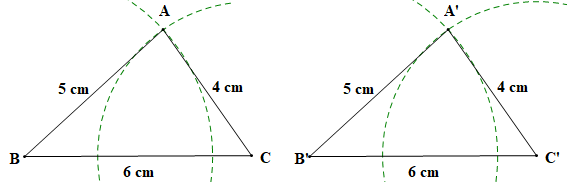
- Dùng thước đo góc ta được kết quả
- Hai tam giác ABC và A'B'C' có:
AB = A'B' (= 5 cm), BC = B'C' (= 6 cm), CA = C'A' (= 4 cm);
.
Vậy hai tam giác ABC và A'B'C' có các cạnh và các góc tương ứng bằng nhau.
Do đó
Câu hỏi trang 66 Toán 7 Tập 1: Trong Hình 4.15, những cặp tam giác nào bằng nhau?
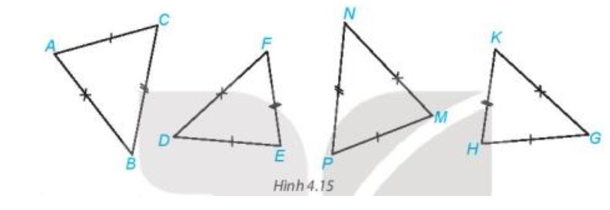
Lời giải:
Xét tam giác ABC và tam giác MNP có:
AB = MN, BC = NP, CA = PM.
Do đó ΔABC = ΔMNP (c – c – c).
Xét tam giác DEF và tam giác GHK có:
DE = GH, EF = HK, FD = KG.
Do đó ΔDEF = ΔGHK (c – c – c).
Vậy trong hình vẽ đã cho, ta có hai cặp tam giác bằng nhau là: tam giác ABC và tam giác MNP, tam giác DEF và tam giác GHK.
Luyện tập 2 trang 66 Toán 7 Tập 1: Cho Hình 4.17, biết AB = AD, BC = DC.

Lời giải:
|
GT |
AB = AD, BC = DC. |
|
KL |
|
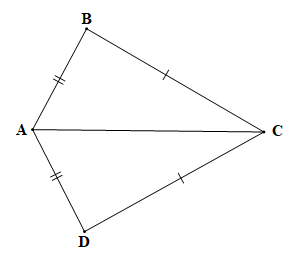
Chứng minh (hình vẽ trên):
Hai tam giác ABC và ADC có:
AB = AD (theo giả thiết);
BC = DC (theo giả thiết);
AC là cạnh chung.
Vậy
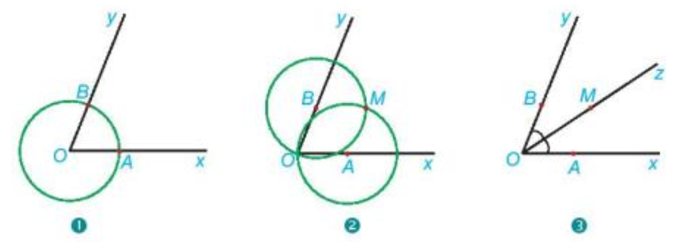
(1) Vẽ đường tròn tâm O cắt Ox, Oy lần lượt tại A và B.
Em hãy giải thích vì sao tia OM là tia phân giác của góc xOy.
Lời giải:
|
GT |
Đường tròn (O) cắt tia Ox tại A, cắt tia Oy tại B; Đường tròn (A; AO) và đường tròn (B; BO) cắt nhau tại M; Tia Oz đi qua M. |
|
KL |
Tia Oz là tia phân giác của góc xOy. |
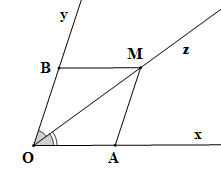
Chứng minh (hình vẽ trên):
Nối BM và AM.
Vì đường tròn (O) cắt tia Ox tại A, cắt tia Oy tại B (theo giả thiết) nên ta có OA = OB.
Đường tròn (A; AO) và đường tròn (B; BO) cắt nhau tại M nên AM = AO và BM = BO.
Mà OA = OB (chứng minh trên).
Do đó AM = BM.
Hai tam giác OAM và OBM có:
OA = OB (chứng minh trên);
AM = BM (chứng minh trên);
OM là cạnh chung.
Vậy
Suy ra (hai góc tương ứng).
Do đó tia Oz là tia phân giác của góc xOy.
Bài 4.4 trang 67 Toán 7 Tập 1: Cho hai tam giác ABC và DEF như Hình 4.18.
Trong các khẳng định sau, khẳng định nào đúng?
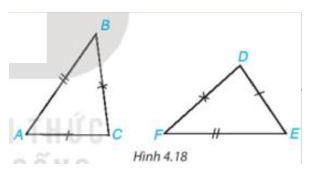
Lời giải:
|
GT |
AB = EF, BC = FD, CA = DE. |
|
KL |
Viết kí hiệu của hai tam giác bằng nhau. |
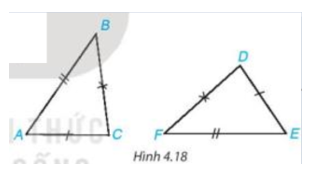
Chứng minh (hình vẽ trên):
Hai tam giác ABC và DEF có:
AB = EF (theo giả thiết);
BC = FD (theo giả thiết);
CA = DE (theo giả thiết).
Vậy
Suy ra (các cặp góc tương ứng).
Tức là đỉnh A tương ứng với đỉnh E, đỉnh B tương ứng với đỉnh F, đỉnh C tương ứng với đỉnh D.
Do đó trong các khẳng định (1), (2), (3) và (4) thì khẳng định đúng là khẳng định (2) và khẳng định 4.
Bài 4.5 trang 67 Toán 7 Tập 1: Trong Hình 4.19, hãy chỉ ra hai cặp tam giác bằng nhau.
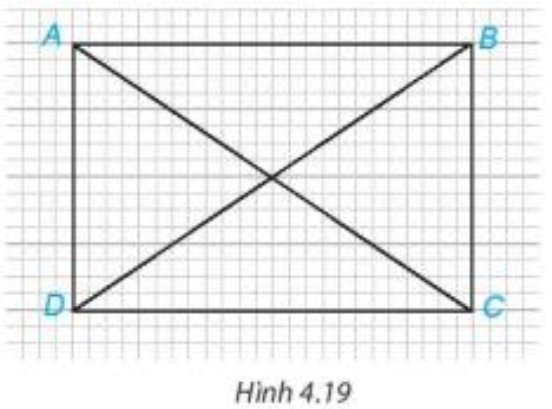
Lời giải:
Trong Hình 4.19, hai cặp tam giác bằng nhau là :
Giải thích:
AB = CD (do ABCD là hình chữ nhật)
BC = DA (do ABCD là hình chữ nhật)
AC chung
Giải thích:
AB = CD (do ABCD là hình chữ nhật)
AD = CB (do ABCD là hình chữ nhật)
BD chung
Bài 4.6 trang 67 Toán 7 Tập 1: Cho Hình 4.20, biết AB = CB, AD = CD,
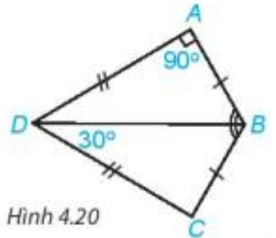
Lời giải:
|
GT |
AB = CB, AD = CD, |
|
KL |
a) b) Tính |
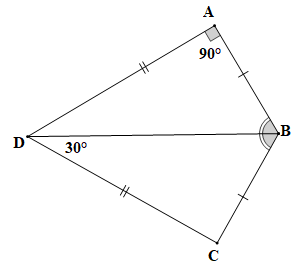
a) Chứng minh (hình vẽ trên):
Hai tam giác ABD và CBD có:
AB = CB (theo giả thiết);
AD = CD (theo giả thiết);
BD là cạnh chung.
Vậy
b) Vì (chứng minh câu a)
Nên (hai góc tương ứng) và (hai góc tương ứng).
Mà (theo giả thiết), do đó
Trong tam giác ABD có nên là tam giác vuông tại A, khi đó hai góc nhọn của tam giác ABD phụ nhau.
Do đó
Suy ra
Tia BD nằm giữa hai tia BA và BC nên .
Mà (chứng minh trên), do đó
Hay
Vậy