Giải Toán 7 (Kết nối tri thức) Luyện tập chung trang 85, trang 86
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 7 Luyện tập chung trang 85, trang 86 sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Luyện tập chung trang 85, trang 86. Mời các bạn đón xem:
Giải bài tập Toán 7 Luyện tập chung trang 85, trang 86
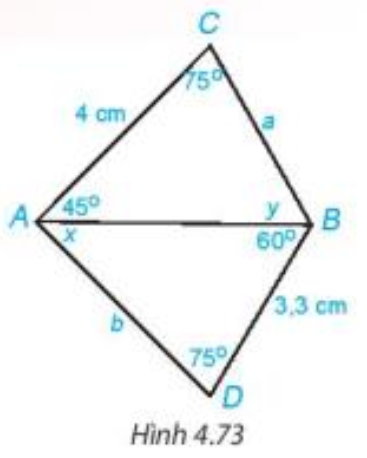
Lời giải:
|
GT |
AC = 4 cm, BD = 3,3 cm;
|
|
KL |
Tìm x, y và tính a, b. |
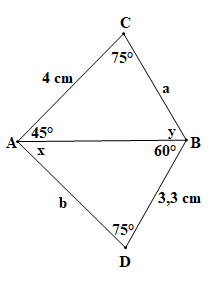
+) Xét tam giác ABD có , theo định lí tổng ba góc trong một tam giác ta có .
Suy ra
Hay x = 180° – 60° – 75°
x = 45°.
Xét tam giác ABC có , theo định lí tổng ba góc trong một tam giác ta có .
Suy ra
Hay y = 180° – 45° – 75°
y = 60°.
+) Xét tam giác ABC và tam giác ABD có:
(cùng có số đo bằng 45°);
AB là cạnh chung;
(cùng có số đo bằng 60°).
Vậy (g.c.g).
Suy ra BC = BD (hai cạnh tương ứng) và AC = AD (hai cạnh tương ứng).
Mà BD = 3,3 cm và AC = 4 cm.
Do đó a = BC = 3,3 cm và b = AD = 4 cm.
Vậy x = 45°, y = 60°, a = 3,3 cm và b = 4 cm.
Lời giải:
|
GT |
; OA = OB, OM = ON, OA > OM. |
|
KL |
a) b) |
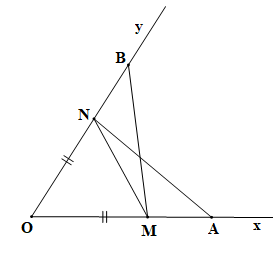
a) Xét tam giác OAN và tam giác OBM có:
OA = OB (theo giả thiết);
là góc chung;
ON = OM (theo giả thiết).
Vậy (c.g.c).
b) Do B, N cùng nằm trên tia Oy, OA = OB, OM = ON và OA > OM (theo giả thiết) nên OB > ON, khi đó OB = ON + NB suy ra NB = OB – ON.
Do A, M cùng nằm trên tia Ox, OA > OM (theo giả thiết) nên OA = OM + MA suy ra MA = OA – OM.
Lại có OA = OB, OM = ON (theo giả thiết) nên OA – OM = OB – ON.
Hay MA = NB.
Từ (chứng minh ở câu a) suy ra AN = BM (hai cạnh tương ứng).
Xét tam giác AMN và tam giác BNM có:
AN = BM (chứng minh trên);
MN là cạnh chung;
MA = NB (chứng minh trên).
Vậy
Bài 4.31 trang 86 Toán 7 Tập 1: Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:
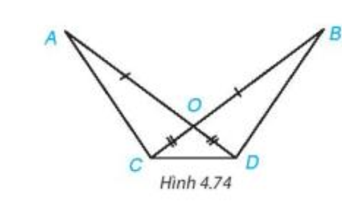
Lời giải:
|
GT |
OA = OB, OC = OD. |
|
KL |
a) AC = BD; b) |
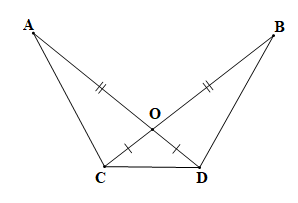
a) Xét tam giác OAC và tam giác OBD có:
OA = OB (theo giả thiết);
(hai góc đối đỉnh);
OC = OD (theo giả thiết).
Vậy (c.g.c).
Suy ra AC = BD (hai cạnh tương ứng).
b) Ta có AD = AO + OD và BC = BO + OC.
Mà OA = OB, OC = OD (theo giả thiết) nên AO + OD = BO + OC hay AD = BC.
Xét tam giác ACD và tam giác BDC có:
AC = BD (chứng minh ở câu a);
AD = BC (chứng minh trên);
CD là cạnh chung.
Vậy (c.c.c).
Lời giải:
|
GT |
vuông tại M, , MA = MB. |
|
KL |
Tam giác ABC là tam giác đều. |
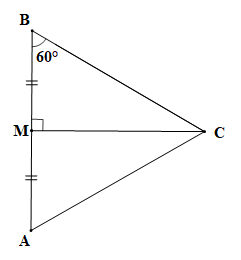
Xét tam giác MBC (vuông tại M) và tam giác MAC (vuông tại M) có:
MB = MA (theo giả thiết);
MC là cạnh chung.
Vậy (hai cạnh góc vuông).
Suy ra (hai góc tương ứng)
Mà nên .
Tam giác ABC có , theo định lí tổng ba góc trong một tam giác ta có
Suy ra hay
Do đó suy ra tam giác ABC đều.
Vậy tam giác ABC đều.


