Giải bài tập Toán 7 Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác 

A. Các câu hỏi trong bài

Mở đầu trang 59 Toán 7 Tập 2:

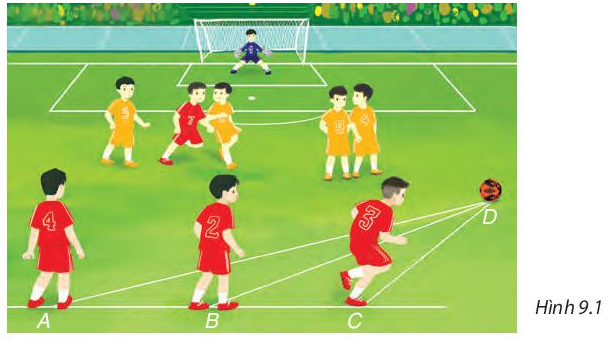
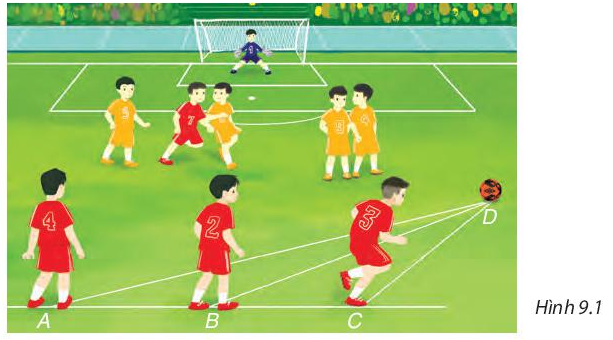
Trong trận bóng đá, trái bóng đang ở vị trí D, ba cầu thủ đứng thẳng hàng tại vị trí A, B, C trên sân với số áo lần lượt là 4, 2, 3 như Hình 9.1. Theo em, cầu thủ nào gần trái bóng nhất, cầu thủ nào xa trái bóng nhất? Tại sao? (Biết rằng góc ACD là góc tù).

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Xét DBCD có góc BCD là góc tù nên góc BCD là góc lớn nhất trong tam giác.

Khi đó BD > CD (1)

Ta có góc ABD là góc ngoài tại đỉnh B của tam giác BCD nên ta có:

$\widehat{ABD}=\widehat{BCD}+\widehat{BDC}>\widehat{BCD}$

Mà góc BCD là góc tù nên góc ABD là góc tù.

Xét DABD có góc ABD là góc tù nên góc ABD là góc lớn nhất trong tam giác.

Khi đó AD > BD (2)

Từ (1) và (2) suy ra AD > BD > CD.

Vậy cầu thủ mang áo số 3 gần trái bóng nhất và cầu thủ mang áo số 4 xa trái bóng nhất.

Hoạt động 1 trang 60 Toán 7 Tập 2:

Quan sát ê ke có góc 60° (H.9.2a). Kí hiệu đỉnh góc vuông là A, đỉnh góc 60° là B và đỉnh góc 30° là C.

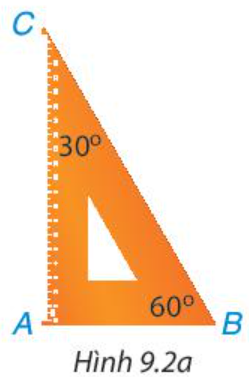
• Sắp xếp độ dài các cạnh theo thứ tự từ bé đến lớn. Sắp xếp độ lớn các góc theo thứ tự từ bé đến lớn.

• Góc lớn nhất đối diện với cạnh nào? Góc bé nhất đối diện với cạnh nào?

Lời giải:

• Sắp xếp độ dài các cạnh theo thứ tự từ bé đến lớn: AB < AC < BC.

Sắp xếp độ lớn các góc theo thứ tự từ bé đến lớn: $\widehat{C}$ < $\widehat{B}$ < $\widehat{A}$.

• Góc A lớn nhất đối diện với cạnh BC.

Góc C bé nhất đối diện với cạnh AB.

Hoạt động 2 trang 60 Toán 7 Tập 2:

Em hãy vẽ một tam giác ABC có AB = 3 cm, AC = 5 cm. Quan sát hình vừa vẽ và dự đoán xem trong hai góc B và C, góc nào lớn hơn.

Lời giải:

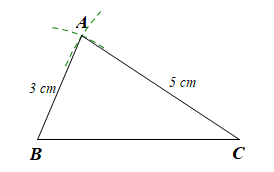
Ta dự đoán trong tam giác ABC với AB = 3 cm và AC = 5 cm thì góc B lớn hơn góc C.

Luyện tập 1 trang 60 Toán 7 Tập 2:

Cho tam giác MNP có độ dài các cạnh: MN = 3 cm, NP = 5 cm, MP = 7 cm. Hãy xác định góc đối diện với từng cạnh rồi sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn.

Lời giải:

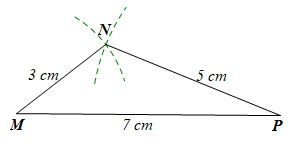
Góc đối diện với cạnh NP là góc M.

Góc đối diện với cạnh MN là góc P.

Góc đối diện với cạnh MP là góc N.

Do MN < NP < MP  (3 cm < 5 cm < 7 cm) nên $\widehat{P}<\widehat{M}<\widehat{N}$.

Các góc của tam giác MNP theo thứ tự từ bé đến lớn là: $\widehat{P};\widehat{M};\widehat{N}.$

Hoạt động 3 trang 61 Toán 7 Tập 2:

Quan sát tam giác ABC trong Hình 9.4a.

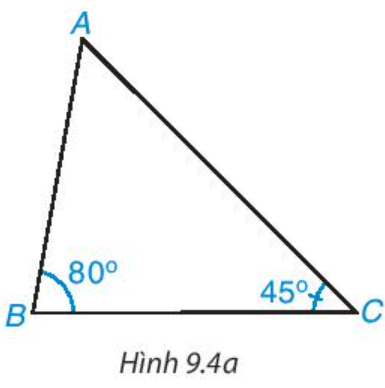
Em hãy dự đoán xem giữa hai cạnh đối diện với hai góc B và C (tức là cạnh AC và AB) thì cạnh nào lớn hơn.

Lời giải:

Cạnh đối diện với góc B và C lần lượt là cạnh AC, AB.

Dự đoán AC > AB.

Hoạt động 3 trang 61 Toán 7 Tập 2:

Quan sát tam giác ABC trong Hình 9.4a.

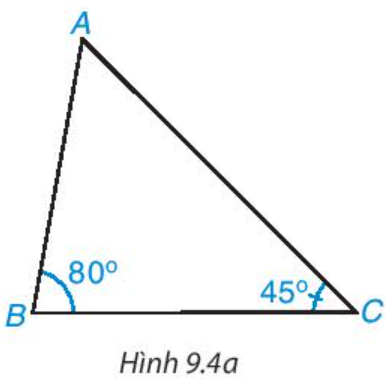
Em hãy đo độ dài hai cạnh AC và AB để kiểm tra lại dự đoán của mình trong HĐ3.

Lời giải:

Sử dụng thước đo độ dài, đo được AB = 3,2 cm; AC = 4,4 cm.

Do 4,4 cm > 3,2 cm nên AC > AB.

Luyện tập 2 trang 61 Toán 7 Tập 2:

Cho tam giác MNP có $\widehat{M}$ = 47°, $\widehat{N}$ = 53°. Hãy viết các cạnh của tam giác đó theo thứ tự độ dài từ bé đến lớn.

Lời giải:

Xét $∆$MNP có $\widehat{M}+\widehat{N}+\widehat{P}=180°$ (tổng ba góc trong một tam giác)

Do đó $\widehat{P}=180°-\widehat{M}-\widehat{N}=180°-47°-53°=80°$.

Do 47° < 53° < 80° nên $\widehat{M}<\widehat{N}<\widehat{P}$.

Cạnh đối diện với góc M, góc N, góc P lần lượt là NP, MP, MN.

Do đó NP < MP < MN.

Vậy các cạnh theo thứ tự từ bé đến lớn là: NP, MP, MN.

Tranh luận trang 61 Toán 7 Tập 2:

Cho tam giác ABC có góc A là góc tù.

Vuông: “Tam giác ABC có cạnh AB lớn nhất”.

Tròn: “Không đúng, tam giác ABC có cạnh BC lớn nhất chứ!”.

Theo em, bạn nào nói đúng? Vì sao?

Lời giải:

Bạn Tròn nói đúng vì:

Tam giác ABC có góc A là góc tù nên góc A là góc lớn nhất trong tam giác.

Cạnh đối diện với góc A trong tam giác ABC là cạnh BC.

Do đó cạnh BC là cạnh lớn nhất trong tam giác ABC.

Vận dụng trang 62 Toán 7 Tập 2:

Em hãy trả lời câu hỏi trong tình huống mở đầu.

Lời giải:

Xét DBCD có góc BCD là góc tù nên góc BCD là góc lớn nhất trong tam giác.

Khi đó BD > CD (1)

Ta có góc ABD là góc ngoài tại đỉnh B của tam giác BCD nên ta có:

$\widehat{ABD}=\widehat{BCD}+\widehat{BDC}>\widehat{BCD}$

Mà góc BCD là góc tù nên góc ABD là góc tù.

Xét DABD có góc ABD là góc tù nên góc ABD là góc lớn nhất trong tam giác.

Khi đó AD > BD (2)

Từ (1) và (2) suy ra AD > BD > CD.

Vậy cầu thủ mang áo số 3 gần trái bóng nhất và cầu thủ mang áo số 4 xa trái bóng nhất.

B. Bài tập

Bài 9.1 trang 62 Toán 7 Tập 2:

Cho tam giác ABC có $\widehat{A}$ = 105°, $\widehat{B}$ = 35°.

a) Tam giác ABC là tam giác gì?

b) Tìm cạnh lớn nhất của tam giác ABC.

Lời giải:

a) Vì $\widehat{A}$ = 105° > 90° nên $\widehat{A}$ là góc tù, do đó tam giác ABC là tam giác tù.

b) Trong tam giác tù ABC có góc A là góc tù nên cạnh đối diện với góc tù A là cạnh lớn nhất.

Mà cạnh đối diện với góc A là cạnh BC.

Vậy cạnh BC là cạnh lớn nhất của tam giác ABC.

Bài 9.2 trang 62 Toán 7 Tập 2:

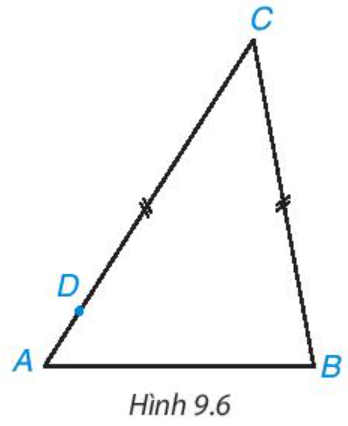
Trong Hình 9.6 có hai đoạn thẳng BC và DC bằng nhau, D nằm giữa A và C. Hỏi kết luận nào trong các kết luận sau là đúng? Tại sao?

a) $\widehat{A}=\widehat{B}$.

b) $\widehat{A}>\widehat{B}$.

c) $\widehat{A}<\widehat{B}$.

Lời giải:

Ta có: AD + DC = AC.

Mà AB = DC nên AC = AD + AB > AB.

Lại có, AC đối diện góc B và AB đối diện góc A.

Do đó, $\widehat{B}>\widehat{A}$ hay $\widehat{A}<\widehat{B}$.

Vậy c đúng.

Bài 9.3 trang 62 Toán 7 Tập 2:

Trong tam giác cân có một góc bằng 96°, hỏi cạnh lớn nhất trong tam giác cân đó là cạnh bên hay cạnh đáy? Vì sao?

Lời giải:

Giả sử ta có tam giác cân ABC với $\widehat{A}$ = 96°.

Ta có: 96° > 90° nên góc A là góc tù.

Do một tam giác không thể có hai góc tù nên đỉnh A chính là đỉnh cân.

Mà trong một tam giác, góc tù là góc lớn nhất trong ba góc nên cạnh đối diện với góc tù là cạnh lớn nhất trong ba cạnh.

Vậy cạnh lớn nhất là cạnh đáy (cạnh đáy là cạnh đối diện với góc ở đỉnh) trong tam giác cân.

Bài 9.4 trang 62 Toán 7 Tập 2:

Ba bạn Mai, Việt và Hà đi đến trường tại địa điểm D lần lượt theo ba con đường AD, BD và CD (H.9.7). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng, B nằm giữa A và C, $\widehat{AC\text{D}}$ là góc tù. Hỏi bạn nào đi xa nhất, bạn nào đi gần nhất? Vì sao?

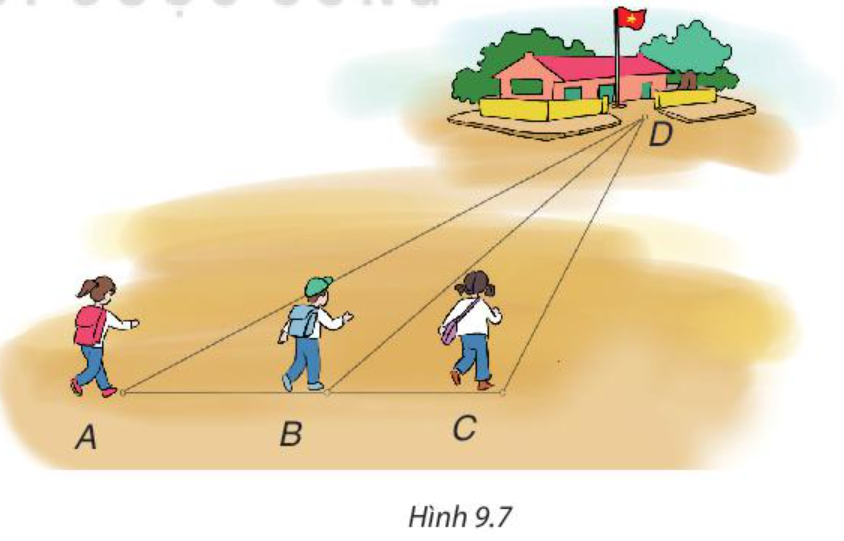
Lời giải:

Xét DBCD có $\widehat{BC\text{D}}$ là góc tù nên $\widehat{BC\text{D}}$ là góc lớn nhất trong tam giác.

Cạnh đối diện với $\widehat{BC\text{D}}$ trong DBCD là cạnh BD.

Do đó cạnh BD là cạnh lớn nhất trong DBCD.

Khi đó BD > CD (1).

Ta có $\widehat{AB\text{D}}$ là góc ngoài tại đỉnh B của DBCD nên $\widehat{AB\text{D}}=\widehat{B\text{D}C}+\widehat{BC\text{D}}>\widehat{BC\text{D}}$.

Mà $\widehat{BC\text{D}}$ là góc tù nên $\widehat{AB\text{D}}$ là góc tù.

Xét DABD có $\widehat{AB\text{D}}$ là góc tù nên $\widehat{AB\text{D}}$ là góc lớn nhất trong tam giác.

Cạnh đối diện với $\widehat{AB\text{D}}$ trong DABD là cạnh AD.

Do đó cạnh AD là cạnh lớn nhất trong DABD.

Khi đó AD > BD (2).

Từ (1) và (2) suy ra AD > BD > CD.

Vậy bạn Mai đi xa nhất, bạn Hà đi gần nhất.

Bài 9.5 trang 62 Toán 7 Tập 2:

Ba địa điểm A, B, C là ba đỉnh của một tam giác ABC với $\widehat{A}$ tù, AC = 500 m. Đặt một loa truyền thanh tại một điểm nằm giữa A và B thì tại C có thể nghe tiếng loa không nếu bán kính để nghe rõ tiếng của loa là 500 m?

Lời giải:

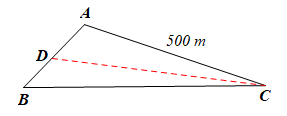
Giả sử D là điểm đặt loa (D nằm giữa A và B).

Xét DACD có $\widehat{CA\text{D}}$ là góc tù nên $\widehat{CA\text{D}}$ là góc lớn nhất trong DACD.

Do đó cạnh đối diện với $\widehat{CA\text{D}}$ là cạnh lớn nhất trong DACD.

Cạnh đối diện với $\widehat{CA\text{D}}$ trong $∆$ACD là cạnh DC.

Do đó DC > AC = 500 m.

Tức là khoảng cách từ vị trí đặt loa D đến điểm C lớn hơn 500.

Mà bán kính để nghe rõ tiếng của loa là 500 m nên tại C không thể nghe rõ tiếng loa.

Vậy nếu đặt loa truyền thanh tại một điểm nằm giữa A và B thì tại C không thể nghe rõ tiếng loa.