Giải bài tập Toán 7 Bài 32: Quan hệ đường giữa đường vuông góc và đường xiên 

A. Các câu hỏi trong bài

Mở đầu trang 63 Toán 7 Tập 2:

Bạn Nam tập bơi ở một bể bơi hình chữ nhật, trong đó có ba đường bơi OA, OB và OC. Biết rằng OA vuông góc với cạnh của bể bơi (H.9,8).

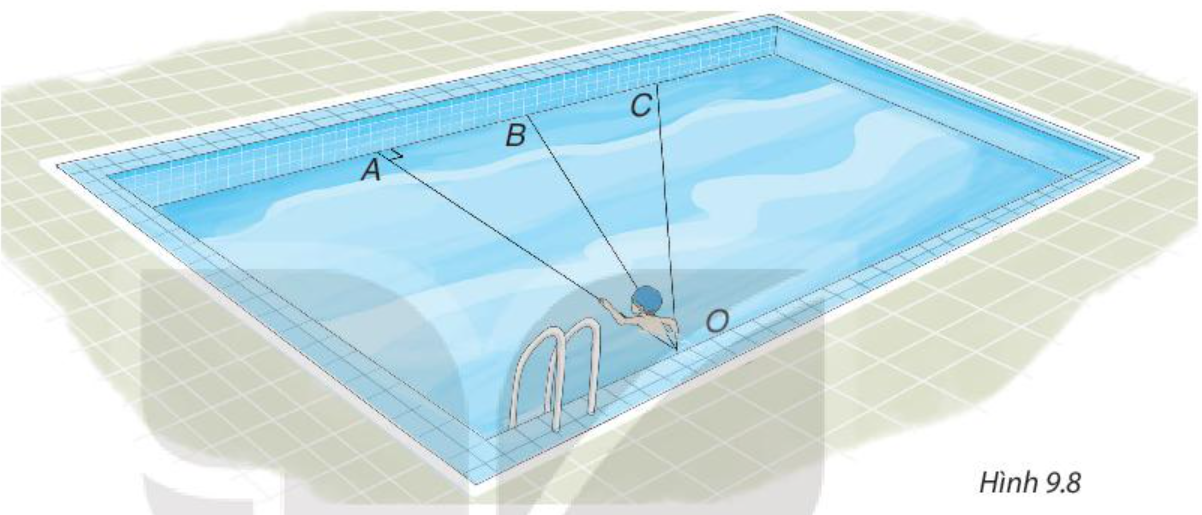
Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì bạn Nam nên chọn đường bơi nào?

Lời giải:

Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì quãng đường bơi phải ngắn nhất.

$∆$OAB có $\widehat{OAB}$ = 90° nên $\widehat{OAB}$ là góc lớn nhất trong $∆$OAB.

Do đó OB > OA (1).

$\widehat{OBC}$ là góc ngoài tại đỉnh B của $∆$OAB nên $\widehat{OBC}=\widehat{BOA}+\widehat{OAB}>\widehat{OAB}$.

Mà $\widehat{OAB}$ = 90° nên $\widehat{OBC}$ > 90° là góc tù.

Xét $∆$BOC có $\widehat{OBC}$ là góc tù nên $\widehat{OBC}$ là góc lớn nhất trong $∆$BOC.

Do đó OC là cạnh lớn nhất trong $∆$BOC.

Khi đó OC > OB (2).

Từ (1) và (2) suy ra OC > OB > OA.

Vậy để bơi sang bờ bên kia nhanh nhất thì Nam nên chọn đường bơi OA.

Hoạt động trang 64 Toán 7 Tập 2:

Cho điểm A không nằm trên đường thẳng d.

a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d.

b) Em hãy giải thích vì sao AH < AM.

Lời giải:

a) 

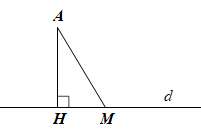
b) Do AH ⊥ d nên $\widehat{AHM}$ = 90°.

Nên tam giác AHM là tam giác vuông có AM là cạnh huyền.

Mà trong tam giác vuông cạnh huyền là cạnh lớn nhất nên AM > AH.

Luyện tập trang 64 Toán 7 Tập 2:

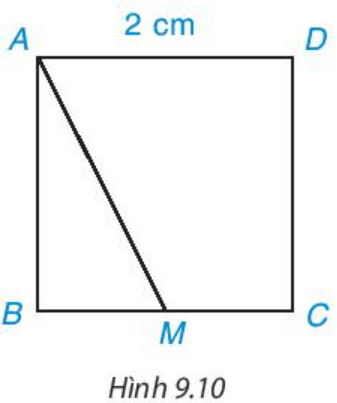
Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10.

a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.

b) So sánh hai đoạn thẳng AB và AM.

c) Tìm khoảng cách từ điểm C đến đường thẳng AB.

Lời giải:

a) Đường vuông góc kẻ từ A đến đường thẳng BC là đoạn thẳng AB.

Đường xiên kẻ từ A đến đường thẳng BC là đoạn thẳng AM.

b) Do AM là đường xiên kẻ từ A đến BC và AB là đường vuông góc kẻ từ A đến BC nên AM > AB.

c) Đường vuông góc kẻ từ điểm C đến đường thẳng AB là đoạn thẳng CB.

Do đó khoảng cách từ C đến đường thẳng AB bằng độ dài đoạn thẳng BC.

Do ABCD là hình vuông nên BC = AD = 2 cm.

Vậy khoảng cách từ C đến đường thẳng AB bằng 2 cm.

Vận dụng trang 64 Toán 7 Tập 2:

Em hãy trả lời câu hỏi trong tình huống mở đầu.

Lời giải:

Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì quãng đường bơi phải ngắn nhất.

Bài toán đưa về tìm đoạn ngắn nhất trong ba đoạn thẳng OA, OB và OC.

Ta có OA là đường vuông góc kẻ từ O đến AC.

          OB và OC là các đường xiên kẻ từ O đến AC

Do đó OA là đoạn thẳng có độ dài ngắn nhất.

Vậy để bơi sang bờ bên kia nhanh nhất thì Nam nên chọn đường bơi OA.

Thử thách nhỏ trang 64 Toán 7 Tập 2:

a) Quan sát Hình 9.11, ta thấy khi M thay đổi trên d, M càng xa H thì độ dài AM càng lớn, tức là nếu HM < HN thì AM < AN. Hãy chứng minh khẳng định này nhờ quan hệ giữa góc và cạnh đối diện trong tam giác AMN.

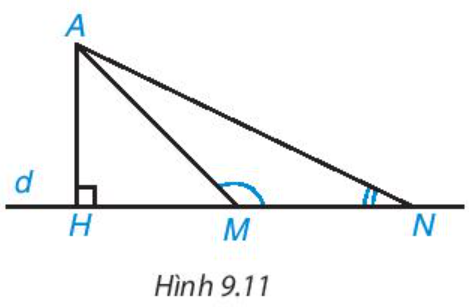
b) Xét hình vuông ABCD và một điểm M tùy ý nằm trên các cạnh của hình vuông. Hỏi với vị trí nào của M thì AM lớn nhất? Vì sao?

Lời giải:

a) Xét DAHM có HM < HN thì $\widehat{AMN}$ là góc ngoài tại đỉnh M của $∆$AHM

Do đó $\widehat{AMN}=\widehat{AHM}+\widehat{HAM}>\widehat{AHM}$.

Mà $\widehat{AHM}=90°$ nên $\widehat{AMN}>90°$ là góc tù.

Xét DAMN có $\widehat{AMN}$ là góc tù nên $\widehat{AMN}$ là góc lớn nhất trong $∆$AMN.

Do đó AN là cạnh lớn nhất trong $∆$AMN hay AM < AN.

b)

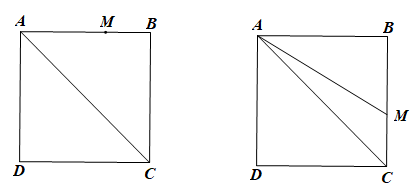
• Nếu M nằm trên AB thì AM ≤ AB.

Tương tự, nếu M nằm trên AD thì AM ≤ AD.

Mà AB = AD (do ABCD là hình vuông)

Do đó nếu M nằm trên cạnh AB hoặc AD thì AM ≤ AB (1).

• Nếu M nằm trên BC thì BM ≤ BC

Theo câu a, khi đó ta có AM ≤ AC.

Tương tự, nếu M nằm trên DC thì AM ≤ AC

Do đó nếu M nằm trên cạnh BC hoặc DC thì AM ≤ AC (2).

• Ta có AB là đường vuông góc kẻ từ A đến BC, AC là đường xiên kẻ từ A đến BC nên

AC ≥ AB (3).

Do đó từ (1), (2) và (3) suy ra AM ≤ AB ≤ AC.

Khi đó AM lớn nhất khi AM = AC, tức điểm M trùng điểm C.

Vậy điểm M trùng điểm C thì AM lớn nhất.

B. Bài tập

Bài 9.6 trang 65 Toán 7 Tập 2:

Chiều cao của tam giác ứng với một cạnh của nó có phải là khoảng cách từ đỉnh đối diện đến đường thẳng chứa cạnh đó không?

Lời giải:

Giả sử tam giác ABC có AH là đường cao ứng với cạnh BC.

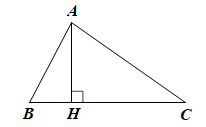
Khi đó AH là khoảng cách từ A đến đường thẳng BC.

Vậy chiều cao của tam giác ứng với một cạnh của nó là khoảng cách từ đỉnh đối diện đến đường thẳng chứa cạnh đó.

Bài 9.7 trang 65 Toán 7 Tập 2:

Cho hình vuông ABCD. Hỏi trong bốn đỉnh của hình vuông

a) Đỉnh nào cách đều hai điểm A và C?

b) Đỉnh nào cách đều hai đường thẳng AB và AD?

Lời giải:

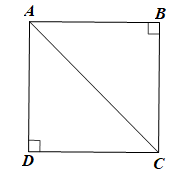
a) Do ABCD là hình vuông nên AB = BC = CD = DA.

Do DA = DC nên điểm D cách đều hai điểm A và C.

Do BA = BC nên điểm B cách đều hai điểm A và C.

Vậy hai đỉnh B và D cách đều hai điểm A và C.

b) Ta có CB là khoảng cách từ C đến AB, CD là khoảng cách từ C đến AD.

Do BC = CD nên khoảng cách từ C đến AB bằng khoảng cách từ C đến AD.

Do đó C là điểm cách đều hai đường thẳng AB và AD.

Ta cũng có AB ⊥ AD tại A nên điểm A cũng cách đều hai đường thẳng AB và AD.

Vậy hai đỉnh C, A cách đều hai đường thẳng AB và AD.

Bài 9.8 trang 65 Toán 7 Tập 2:

Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.12).

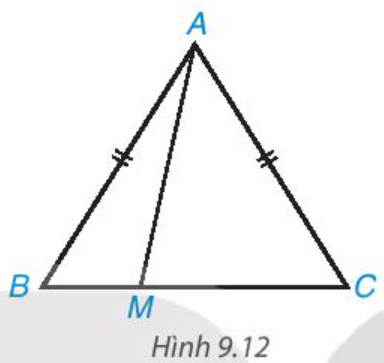
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.

b) Chứng minh rằng với mọi điểm M thì AM < AB.

Lời giải:

a) Kẻ AH vuông góc với BC tại H.

Khi M di chuyển trên BC thì tạo ra các đường xiên AM kẻ từ A xuống BC.

Trường hợp đặc biệt khi M trùng với H thì AM là đường vuông góc.

Mà trong các đường xiên và đường vuông góc kẻ từ một điểm nằm ngoài đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.

Vậy M là chân đường cao kẻ từ A đến BC thì độ dài AM nhỏ nhất.

b)

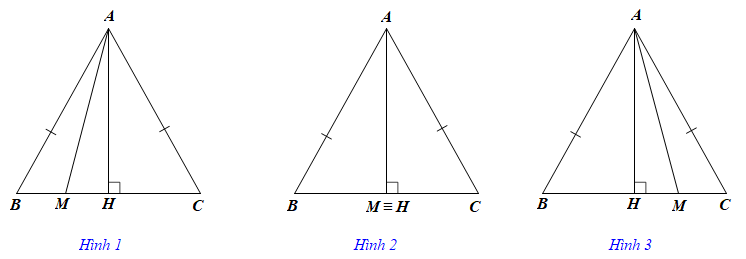
Ta xét các trường hợp sau:

• M nằm giữa B và H (Hình 1):

$\widehat{AMB}$ là góc tù nên $∆$ABM là tam giác tù.

Khi đó cạnh AB đối diện với $\widehat{AMB}$ là cạnh lớn nhất của $∆$ABM.

Hay AM < AB (1)

• M trùng với H (Hình 2):

AH, AB lần lượt là đường vuông góc và đường xiên kẻ từ A đến BC.

Khi đó AH là đường ngắn nhất nên AH = AM < AB (2)

• M nằm giữa H và C (Hình 3):

$\widehat{AMC }$ là góc tù nên $∆$AMC là tam giác tù.

Khi đó cạnh AC đối diện với $\widehat{AMC}$ là cạnh lớn nhất của $∆$AMC.

Hay AM < AC

Mà AB = AC (do $∆$ABC cân tại A).

Do đó AM < AB (3)

Từ (1), (2) và (3) ta có AM < AB.

Vậy AM < AB.

Bài 9.9 trang 65 Toán 7 Tập 2:

Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC (M, N không phải là đỉnh của tam giác) (H.9.13). Chứng minh rằng MN < BC.

(Gợi ý. So sánh MN với NB, NB với BC).

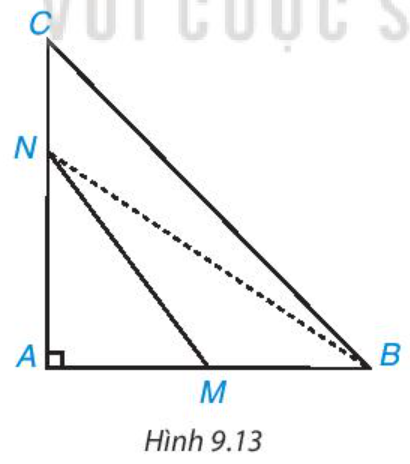
Lời giải:

Ta có $\widehat{NMB}$ là góc ngoài tại đỉnh M của $∆$AMN nên

$\widehat{NMB}=\widehat{ANM}+\widehat{NAM}>\widehat{NAM}$ 

Mà $\widehat{NAM}=90°$do đó $\widehat{NMB}>90°$ là góc tù.

DNMB có $\widehat{NMB}$ là góc tù nên $\widehat{NMB}$ là góc lớn nhất trong $∆$NMB.

Do đó cạnh NB là cạnh lớn nhất trong $∆$NMB.

Khi đó MN < NB (1).

$\widehat{CNB}$ là góc ngoài tại đỉnh N của $∆$ANB nên $\widehat{CNB}=\widehat{NBA}+\widehat{BAN}>\widehat{BAN}$.

Mà $\widehat{BAN}=90°$ do đó $\widehat{CNB}>90°$ là góc tù.

$∆$CNB có $\widehat{CNB}$ là góc tù nên $\widehat{CNB}$ là góc lớn nhất trong $∆$CNB.

Do đó cạnh BC là cạnh lớn nhất trong $∆$CNB.

Khi đó NB < BC (2).

Từ (1) và (2) ta có MN < NB < BC.

Vậy MN < BC.