Giải bài tập Toán 7 Luyện tập chung trang 83

Bài 9.31 trang 83 Toán 7 Tập 2:

Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.

Lời giải:

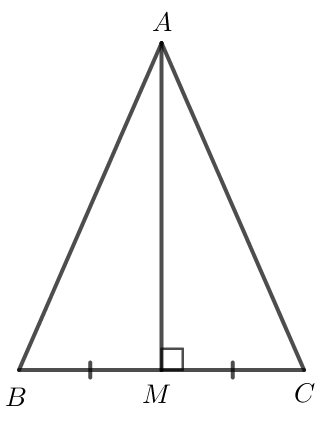
Giả sử $∆$ABC có AM vừa là đường trung tuyến, vừa là đường cao xuất phát từ đỉnh A.

Do AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC.

Do đó BM = CM.

Xét $∆$ABM và $∆$ACM có:

$\widehat{AMB}=\widehat{AMC}={90}^o$,

AM là cạnh chung.

BM = CM (chứng minh trên).

Suy ra $∆$ABM và $∆$ACM (hai cạnh góc vuông).

Do đó AB = AC (hai cạnh tương ứng).

Tam giác ABC có AB = AC nên tam giác ABC cân tại A.

Bài 9.32 trang 83 Toán 7 Tập 2:

Cho ba điểm phân biệt thẳng hàng A, B, C. Gọi d là đường thẳng vuông góc với đường thẳng AB tại A. Với điểm M thuộc d, M khác A, vẽ đường thẳng CM. Qua B kẻ đường thẳng vuông góc với đường thẳng CM, cắt d tại N. Chứng minh đường thẳng BM vuông góc với đường thẳng CN.

Lời giải:

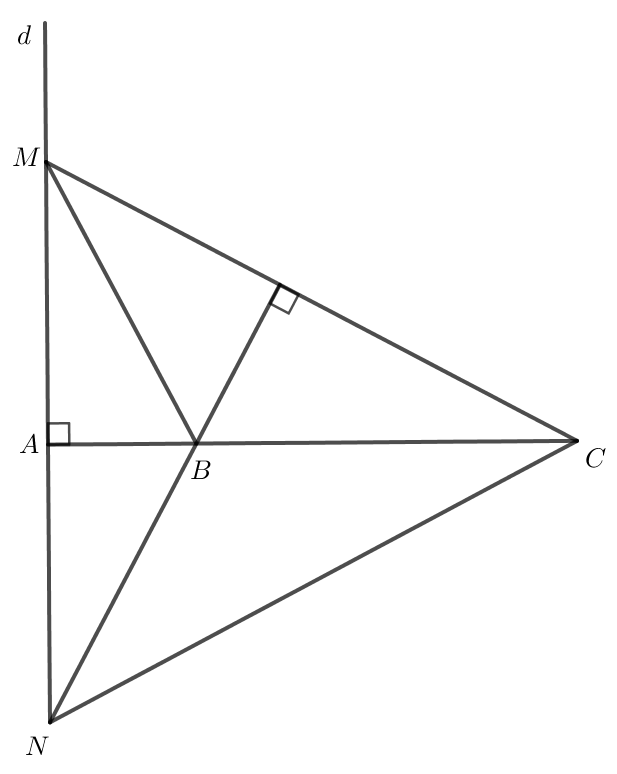
Xét DMNC có NB ⊥ MC, CB ⊥ MN.

Mà NB cắt CB tại B nên B là trực tâm của $∆$MNC.

Do đó BM ⊥ CN.

Bài 9.33 trang 83 Toán 7 Tập 2:

Có một mảnh tôn hình tròn cần đục một lỗ ở tâm. Làm thế nào để xác định được tâm của mảnh tôn đó?

Lời giải:

Ta thực hiện theo các bước sau:

Bước 1. Xác định ba điểm A, B, C nằm trên rìa mảnh tôn.

Bước 2. Xác định ba đường trung trực của tam giác ABC.

Bước 3. Xác định giao điểm của ba đường trung trực của tam giác ABC.

Điểm đó là tâm của mảnh tôn.

Bài 9.34 trang 83 Toán 7 Tập 2:

Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của tia AC. Chứng minh rằng nếu đường thẳng chứa tia At song song với đường thẳng BC thì tam giác ABC cân tại A.

Lời giải:

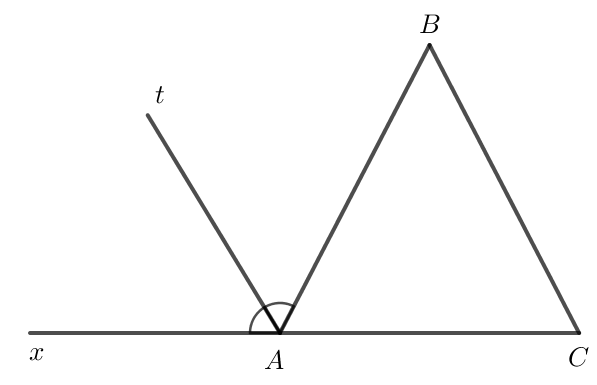
Gọi Ax là tia đối của tia AC.

Do At là tia phân giác của $\widehat{BAx}$ nên $\widehat{xAt}=\widehat{tAB}$.

Do At // BC nên $\widehat{xAt}=\widehat{ACB}$ (hai góc đồng vị).  

Do At // BC nên $\widehat{tAB}=\widehat{ABC}$ (hai góc so le trong).

Mà $\widehat{xAt}=\widehat{tAB}$ nên $\widehat{ABC}=\widehat{ACB}$.

Xét $∆$ABC có $\widehat{ABC}=\widehat{ACB}$ nên $∆$ABC cân tại A.

Bài 9.35 trang 83 Toán 7 Tập 2:

Kí hiệu S_ABC là diện tích tam giác ABC. Gọi G là trọng tâm của tam giác ABC, M là trung điểm của BC.

a) Chứng minh S_GBC = $\frac{1}{3}$S_ABC.

Gợi ý. Sử dụng GM = $\frac{1}{3}$AM để chứng minh S_GBM = $\frac{1}{3}$S_ABM, S_GCM = $\frac{1}{3}$S_ACM.

b) Chứng minh S_GCA = S_GAB = $\frac{1}{3}$S_ABC.

Nhận xét. Từ bài tập trên ta có: S_GBC = S_GCA = S_GAB = $\frac{1}{3}$S_ABC, điều này giúp ta cảm nhận tại sao có thể đặt thăng bằng miếng bìa hình tam giác trên giá nhọn đặt tại trọng tâm của tam giác đó.

Lời giải:

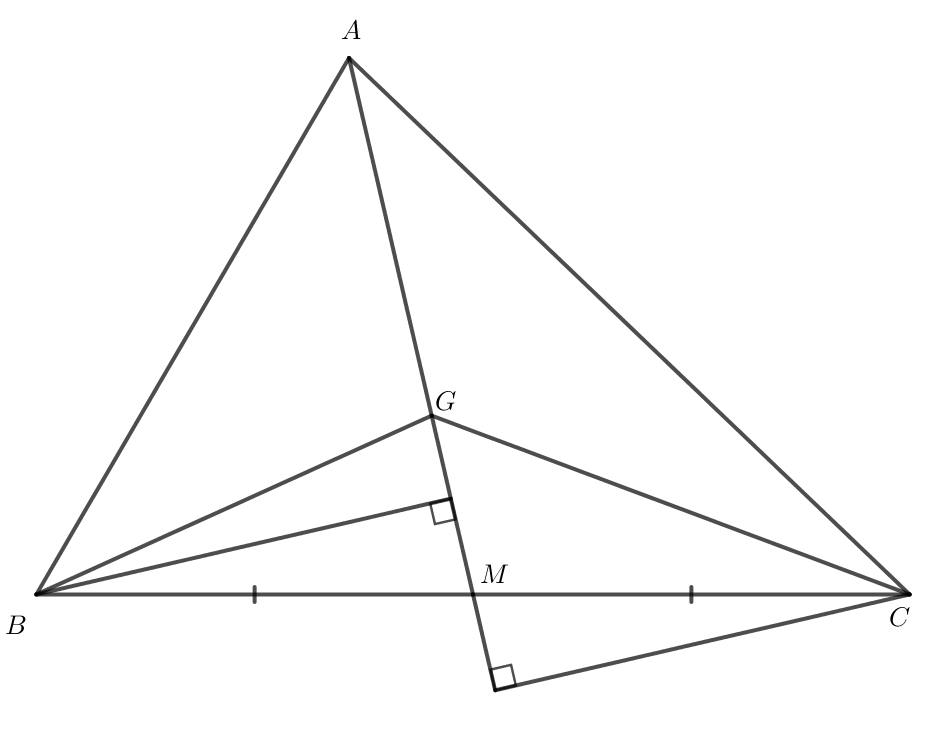
a) Do G là trọng tâm của tam giác ABC và M là trung điểm của BC nên GM = $\frac{1}{3}$AM.

$∆$ABM và $∆$MBG có chung đường cao kẻ từ B đến AM nên tỉ số diện tích giữa MBG và $∆$ABM bằng tỉ số của hai đáy GM và AM.

Ta có GM = $\frac{1}{3}$AM nên S_MBG = $\frac{1}{3}$S_ABM.

$∆$ACM và $∆$MCG có chung đường cao kẻ từ C đến AM nên tỉ số diện tích giữa $∆$MCG và $∆$ACM bằng tỉ số của hai đáy GM và AM.

Ta có GM = $\frac{1}{3}$AM nên S_MCG = $\frac{1}{3}$S_ACM.

Do đó S_MBG + S_MCG = $\frac{1}{3}$S_ABM + $\frac{1}{3}$S_ACM

Hay S_GBC = $\frac{1}{3}$(S_ABM + S_ACM) = $\frac{1}{3}$S_ABC.

b) Chứng minh tương tự câu a:

Do G là trọng tâm của $∆$ABC nên AG = 2GM suy ra S_GCA = 2S_MCG; S_GAB = 2S_MBG.

Do BC = 2MB = 2MC nên S_GBC = 2S_MCG = 2S_MBG.

Do đó S_GCA = S_GAB = S_GBC = $\frac{1}{3}$S_ABC.