Cho tam giác MBC vuông tại M có góc B = 60 °. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều
Lời giải Bài 4.32 trang 86 Toán 7 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7 Tập 1.
Giải Toán 7 Luyện tập chung trang 85, trang 86
Bài 4.32 trang 86 Toán 7 Tập 1: Cho tam giác MBC vuông tại M có Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.
Lời giải:
|
GT |
vuông tại M, , MA = MB. |
|
KL |
Tam giác ABC là tam giác đều. |
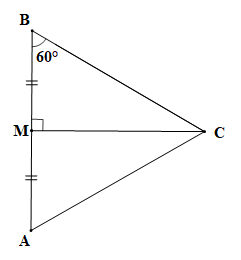
Xét tam giác MBC (vuông tại M) và tam giác MAC (vuông tại M) có:
MB = MA (theo giả thiết);
MC là cạnh chung.
Vậy (hai cạnh góc vuông).
Suy ra (hai góc tương ứng)
Mà nên .
Tam giác ABC có , theo định lí tổng ba góc trong một tam giác ta có
Suy ra hay
Do đó suy ra tam giác ABC đều.
Vậy tam giác ABC đều.
Xem thêm lời giải bài tập Toán 7 Tập 1 Kết nối tri thức hay, chi tiết khác:
Bài 4.29 trang 86 Toán 7 Tập 1: Cho Hình 4.73. Hãy tìm số đo x, y của các góc và độ dài a, b của các đoạn thẳng trên hình vẽ
Bài 4.30 trang 86 Toán 7 Tập 1: Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM. Chứng minh rằng: a) ΔOAN = ΔOBM ; b) ΔAMN = ΔBNM
Bài 4.31 trang 86 Toán 7 Tập 1: Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng: a) AC = BD; b) ΔACD = ΔBDC
Bài 4.32 trang 86 Toán 7 Tập 1: Cho tam giác MBC vuông tại M có góc B = 60 °. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều


