Giải Toán 6 Chân trời sáng tạo Bài 7: Dấu hiệu chia hết cho 2, cho 5
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 6 Bài 7: Dấu hiệu chia hết cho 2, cho 5 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 6 Bài 7. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài 7: Dấu hiệu chia hết cho 2, cho 5
Lời giải:
Sau bài này chúng ta sẽ biết:
- Các số có chữ số tận cùng là 0, 2, 4, 6, 8(hay là các chữ số chẵn) thì chia hết cho 2.
- Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5.
Hoạt động khám phá 1 trang 24 Toán lớp 6 Tập 1:
Trong một đại hội thể thao có các đội và số người tham gia trong các bảng sau:
Trong các đội đã cho, đội nào xếp được thành hai hàng có số người bằng nhau?
Lời giải:
Ta có: 10:2 = 5
22:2 = 11
14:2 = 7
17:2 = 8 (dư 1)
23:2 = 11 (dư 1)
55:2 = 27 (dư 1)
36:2 = 18
28:2 = 14
19:2 = 9 (dư 1)
Do đó các số chia hết cho 2 là: 10; 22; 14; 36; 28.
Đội có số người xếp được thành hai hàng nếu số người của đội đó chia hết cho 2 là: đội A, đội B, đội C, đội H, đội I.
Thực hành 1 trang 25 Toán lớp 6 Tập 1:
a) Viết hai số lớn hơn 1000 và chia hết cho 2.
b) Viết hai số lớn hơn 100 và không chia hết cho 2.
Lời giải:
a) Hai số lớn hơn 1 000 và chia hết cho 2 là: 1 002, 1 004. ( các em có thể liệt kê các số khác miễn là số đó lớn hơn 1000 và có chữ số tận cùng là 0, 2, 4, 6, 8).
b) Hai số lớn hơn 100 và không chia hết cho 2 là: 101, 103. ( các em có thể liệt kê các số khác miễn là số đó lớn hơn 100 và có chữ số tận cùng khác 0, 2, 4, 6, 8).
Hoạt động khám phá 2 trang 25 Toán lớp 6 Tập 1: Chọn các số chia hết cho 5 ở dưới đây:
10; 22; 15; 27; 33; 25; 19; 36; 95.
Có nhận xét gì về các chữ số tận cùng (chữ số hàng đơn vị) của các số chia hết cho 5 em vừa chọn.
Lời giải:
Ta có: 10:5 = 2 nên 10 chia hết cho 5
22:5 = 4 (dư 2) nên 22 không chia hết cho 5
15:5 = 3 nên 15 chia hết cho 5
27:5 = 5( dư 2) nên 27 không chia hết cho 5
33:5 = 6 (dư 3) nên 33 không chia hết cho 5
25:5 = 5 nên 25 chia hết cho 5
19:5 = 3 (dư 4) nên 19 không chia hết cho 5
36:5 = 7 (dư 1) nên 36 không chia hết cho 5
95:5 = 19 nên 95 chia hết cho 5.
Các số chia hết cho 5 là: 10; 15; 25; 95.
Nhận xét: các số trên có chữ số tận cùng (chữ số hàng đơn vị) là 0 hoặc 5.
Lời giải:
Vì chữ số cần điền vào dấu * nằm ở vị trí tận cùng của số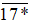 
nên:
a) Để số đã cho chia hết cho 2 thì dấu * được thay thế bởi một trong các số 0; 2; 4; 6; 8.
b) Để số đã cho chia hết cho 5 thì dấu * được thay thế bởi 0 hoặc 5.
c) Để số đã cho chia hết cho cả 2 và 5 thì dấu * được thay thế bởi số 0.
Bài 1 trang 25 Toán lớp 6 Tập 1: Trong những số sau: 2 023; 19 445; 1 010, số nào:
Lời giải:
a) Số chia hết cho 2 là: 1 010 (Vì 1 010 có chữ số tận cùng là 0).
b) Số chia hết cho 5 là: 19 445; 1 010 (Vì 19 445, 1 010 có chữ số tận cùng là 0 và 5).
c) Số chia hết cho 10 là: 1 010 (Vì 1 010 vừa chia hết cho 2 và 5 nên 1 010 chia hết cho 10).
Lời giải:
a) Số 146 có tận cùng là 6 nên 146 chia hết cho 2, 550 có chữ số tận cùng là 0 nên 550 chia hết cho 2. Do đó 146 + 550 chia hết cho 2 (theo dấu hiệu chia hết của một tổng).
b) Số 575 có tận cùng là 5 nên 575 chia hết cho 5, 40 có tận cùng là 0 nên 40 chia hết cho 5. Do đó 575 – 40 chia hết cho 5.
c) Ta có: 3.4.5 = 3.2.2.5 chia hết cho 2 và chia hết cho 5, nhưng 83 có chữ số tận cùng là 3 nên 83 không chia hết cho 2 và không chia hết cho 5. Do đó 3.4.5 + 83 không chia hết cho 2, không chia hết cho 5.
d) Vì 7.5.6 ⋮ 2 và 35.4 ⋮ 2 nên 7.5.6 – 35.4 ⋮ 2.
Vì 7.5.6 ⋮ 5 và 35.4 ⋮ 5 nên 7.5.6 – 35.4 ⋮ 5.
Do đó 7.5.6 – 35.4 chia hết cho 2 và chia hết cho 5.
Bài 3 trang 25 Toán lớp 6 Tập 1: Lớp 6A, 6B, 6C, 6D lần lượt có 35, 36, 39, 40 học sinh.
a) Lớp nào có thể chia thành 5 tổ có cùng số tổ viên?
b) Lớp nào có thể chia tất cả các bạn thành các đôi bạn học tập?
Lời giải:
a) Để biết lớp nào có thể chia thành 5 tổ có cùng số tổ viên thì ta xét xem số học sinh của lớp đó có chia hết cho 5 hay không.
Ta có: 35 ⋮ 5 (vì 35 có chữ số tận cùng là 5)
40 ⋮ 5 (vì 40 có chữ số tận cùng là 0)
Nên: Lớp 6A và 6D có thể chia thành 5 tổ mà các tổ có cùng số tổ viên
b) Một đôi bạn thì gồm 2 bạn nên muốn biết lớp nào có thể chia tất cả các bạn thành các đôi bạn học tập thì ta xét xem số học sinh của mỗi lớp đó có chia hết cho 2 hay không.
Ta có: 36 ⋮ 2 (Vì 36 có chữ số tận cùng là 6)
40 ⋮ 2 (Vì 40 có chữ số tận cùng là 0)
Nên: Lớp 6B và 6D có thể chia tất cả các bạn thành các đôi bạn học tập.
Lời giải:
Vì 19 không chia hết cho 5 (do 19 có chữ số tận cùng là 9), nhưng 20 lại chia hết cho 5 (do 20 có chữ số tận cùng là 0).
Vì vậy bà Huệ không thể chia số quả xoài và quýt thành 5 phần bằng nhau (có cùng số xoài, có cùng số quýt mà không được cắt quả).
Giải Toán 6 Chân trời sáng tạo Bài 8: Dấu hiệu chia hết cho 3, cho 9
Giải Toán 6 Chân trời sáng tạo Bài 9: Ước và bội
Giải Toán 6 Chân trời sáng tạo Bài 10: Số nguyên tố, Hợp số, Phân tích một số ra thừa số nguyên tố
Giải Toán 6 Chân trời sáng tạo Bài 11: Hoạt động thực hành và trải nghiệm
Giải Toán 6 Chân trời sáng tạo Bài 12: Ước chung, Ước chung lớn nhất
Bài viết liên quan
- Giải Toán 6 Chân trời sáng tạo Bài 5: Thứ tự thực hiện các phép tính
- Giải Toán 6 Chân trời sáng tạo Bài 6: Chia hết và chia có dư Tính chất chia hết của một tổng
- Giải Toán 6 Chân trời sáng tạo Bài 8: Dấu hiệu chia hết cho 3, cho 9
- Giải Toán 6 Chân trời sáng tạo Bài 9: Ước và bội
- Giải Toán 6 Chân trời sáng tạo Bài 10: Số nguyên tố, Hợp số, Phân tích một số ra thừa số nguyên tố
