Giải Toán 6 Chân trời sáng tạo Bài 1: Phép thử nghiệm - Sự kiện
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 6 Bài 1: Phép thử nghiệm - Sự kiện sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 6 Bài 1. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài 1: Phép thử nghiệm - Sự kiện
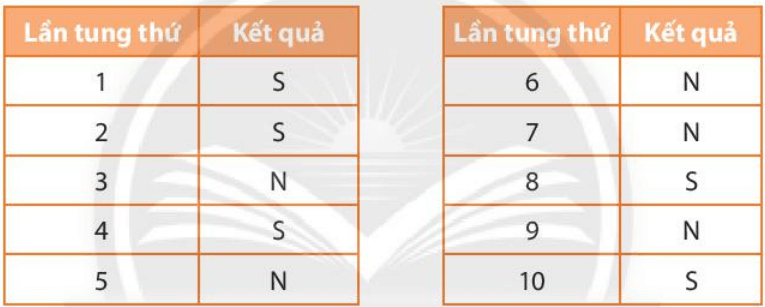
Bạn Hùng tung đồng xu một số lần và ghi lại kết quả vào bảng sau:
– Bạn Hùng đã tung đồng xu bao nhiêu lần và kết quả của lần tung thứ nhất và thứ năm?
- Có bao nhiêu kết quả khác nhau có thể xảy ra khi bạn Hùng tung đồng xu? Đó là các kết
- Kết quả của lần bốc thăm thứ 5 và thứ 6?
- Có bao nhiêu kết quả khác nhau có thể xảy ra trong mỗi lần bốc thăm? Đó là các kết quả nào?
Hãy thực hiện hoạt động trên và lập bảng ghi lại kết quả thu được.
Lời giải:
a) Dựa vào kết quả ở bảng thứ nhất, ta có:
- Bạn Hùng đã tung đồng xu từ lần thứ nhất đến lần thứ 10 hay bạn Hùng đã tung đồng xu 10 lần.
Kết quả của lần thứ nhất là mặt sấp (S), lần thứ năm là mặt ngửa (N).
- Có 2 kết quả khác nhau có thể xảy ra. Đó là kết quả đồng xu hiện ra mặt sấp hoặc đồng xu hiện ra mặt ngửa.
b) Dựa vào kết quả ở bảng thứ hai, ta có:
- Kết quả lần bốc thăm thứ 5 là số 4 và lần bốc thăm thứ 6 là số 1.
- Có 4 kết quả khác nhau có thể xảy ra. Đó là các kết quả bốc được lá thăm số 1; 2; 3; 4.
- Bốc được lá thăm ghi số nhỏ hơn 5.
- Bốc được lá thăm ghi số chia hết cho 5.
Lời giải:
Trong phép thử ở hoạt động khám phá 1 câu b, các kết quả bốc được lá thăm số: 1; 2; 3; 4.
- Ta thấy: các số trên lá thăm đều nhỏ hơn 5.
Vậy sự kiện “Bốc được lá thăm ghi số nhỏ hơn 5” có thể xảy ra.
- Các lá thăm ghi số lẻ trong bảng trên là: 1 và 3.
Các lá thăm ghi số chẵn trong bảng trên là: 2 và 4.
Khi bốc ngẫu nhiên một lá thăm thì có thể bốc được lá thăm ghi số lẻ hoặc số chẵn.
Vậy sự kiện “Bốc được lá thăm ghi số lẻ” có thể xảy ra.
- Trong các lá thăm số 1; 2; 3; 4 không có số nào chia hết cho 5.
Vậy sự kiện “Bốc được lá thăm ghi số chia hết cho 5” không xảy ra.
- Số của thẻ lấy ra là số chẵn.
- Số của thẻ lấy ra chia hết cho 10.
- Số của thẻ lấy ra nhỏ hơn 10.
Lời giải:
Có 9 tấm thẻ giống nhau được đánh số từ 1 đến 9. Khi lấy ra một thử từ hộp thì các kết quả có thể xảy ra là tấm thẻ ghi số: 1; 2; … ; 9.
Trong 9 tấm thẻ lấy ra từ hộp:
Các tấm thẻ có ghi số chẵn là: 2; 4; 6; 8.
Các tấm thẻ có ghi số lẻ là: 1; 3; 5; 7; 9.
Khi lấy ra một tấm thẻ từ hộp thì tấm thẻ đó có thể là số chẵn hoặc số lẻ.
- Sự kiện “Số của thẻ lấy ra là số chẵn” có thể xảy ra.
- Sự kiện “Số của thẻ lấy ra là số lẻ” có thể xảy ra
- Sự kiện “Số của thẻ lấy ra chia hết cho 10” không thể xảy ra. Vì trong 9 tấm thẻ được đánh số từ 1 đến 9, không có tấm thẻ nào ghi số chia hết cho 10.
- Sự kiện “Số của thẻ lấy ra nhỏ hơn 10” chắc chắn xảy ra. Vì cả 9 tấm thẻ được đánh số từ 1 đến 9 đều ghi số nhỏ hơn 10.
a) Lấy ra 1 bút từ hộp có 1 bút chì và 1 bút bi.
b) Bạn Lan chọn một ngày trong tuần để học bơi.
Lời giải:
a) Lấy ra 1 bút từ hộp có 1 bút chì và 1 bút bi.
Các kết quả có thể xảy ra là: lấy ra 1 bút chì hoặc lấy ra 1 bút bi.
b) Các ngày trong tuần gồm: Thứ 2, Thứ 3, Thứ 4, Thứ 5, Thứ 6, Thứ 7, Chủ nhật.
Bạn Lan chọn một ngày trong tuần để học bơi nghĩa là bạn Lan sẽ chọn ra một ngày để đi bơi trong số 7 ngày trên.
Vậy tập hợp các kết quả có thể xảy ra là:
|
Kết quả |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Ngày được chọn |
Thứ 2 |
Thứ 3 |
Thứ 4 |
Thứ 5 |
Thứ 6 |
Thứ 7 |
Chủ nhật |
a) Lấy ra 1 bút từ hộp có 1 bút chì và 1 bút bi.
b) Bạn Lan chọn một ngày trong tuần để học bơi.
Lời giải:
a) Lấy ra 1 bút từ hộp có 1 bút chì và 1 bút bi.
Các kết quả có thể xảy ra là: lấy ra 1 bút chì hoặc lấy ra 1 bút bi.
b) Các ngày trong tuần gồm: Thứ 2, Thứ 3, Thứ 4, Thứ 5, Thứ 6, Thứ 7, Chủ nhật.
Bạn Lan chọn một ngày trong tuần để học bơi nghĩa là bạn Lan sẽ chọn ra một ngày để đi bơi trong số 7 ngày trên.
Vậy tập hợp các kết quả có thể xảy ra là:
|
Kết quả |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Ngày được chọn |
Thứ 2 |
Thứ 3 |
Thứ 4 |
Thứ 5 |
Thứ 6 |
Thứ 7 |
Chủ nhật |
Em hãy liệt kê tập hợp tất cả các kết quả có thể xảy ra trong mỗi lần quay.
Lời giải:
Sau mỗi lần quay, bóng đều được trả lại lồng để thực hiện lần quay tiếp theo nên quả bóng lọt xuống lỗ là một trong 10 quả ban đầu.
Có 10 quả bóng có cùng kích thước được đánh số từ 0 đến 9. Khi có quả bóng lọt xuống lỗ thì quả bóng đó có thể đánh 1 trong 10 số: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.
Vậy tất cả các kết quả có thể xảy ra trong mỗi lần quay là:
|
Lọt xuống lỗ lần thứ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Số ghi trên quả bóng |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Lời giải:
Một đồng xu có hai mặt là mặt sấp và mặt ngửa.
Ký hiệu: mặt sấp là S, mặt ngửa là N.
Khi tung 1 đồng xu hai lần liên tiếp, có thể xảy ra 4 kết quả là:
- Lần 1 sấp (S), lần 2 sấp (S).
- Lần 1 sấp (S), lần 2 ngửa (N).
- Lần 1 ngửa (N), lần 2 sấp (S).
- Lần 1 ngửa (N), lần 2 ngửa (N).
Vậy các kết quả có thể xảy ra của hoạt động tung một đồng xu hai lần liên tiếp là:
|
Kết quả |
1 |
2 |
3 |
4 |
|
Lần gieo thứ nhất |
S |
S |
N |
N |
|
Lần gieo thứ hai |
S |
N |
S |
N |
Hãy đánh giá xem các sự kiện sau là chắc chắn, không thể hay có thể xảy ra.
a) Tổng số chấm xuất hiện trên hai con xúc xắc bằng 1.
b) Tích số chấm xuất hiện trên hai con xúc xắc bằng 1.
c) Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 1.
d) Hai mặt xuất hiện cùng số chấm.
Lời giải:
Số chấm xuất hiện ở mỗi mặt của con xúc xắc là: 1; 2; 3; 4; 5; 6.
a) Số chấm xuất hiện ở mặt nhỏ nhất của con xúc xắc là 1.
Do đó, tổng số chấm xuất hiện trên hai con xúc xắc nhỏ nhất là: 1 + 1 = 2 (chấm).
Hay tổng số chấm xuất hiện trên hai con xúc xắc luôn lớn hơn hoặc bằng 2.
Vậy sự kiện “Tích số chấm xuất hiện trên hai con xúc xắc bằng 1” không thể xảy ra.
b) Khi số chấm xuất hiện trên mỗi con xúc xắc đều là 1, thì tích số chấm xuất hiện trên hai con xúc xắc là: 1 . 1 = 1 (chấm)
Còn các trường hợp khác tích số chấm xuất hiện trên hai con xúc xắc đều lớn hơn 1.
Vậy sự kiện “Tích số chấm xuất hiện trên hai con xúc xắc bằng 1” có thể xảy ra.
c) Số chấm xuất hiện ở mặt nhỏ nhất của con xúc xắc là 1.
Do đó, tổng số chấm xuất hiện trên hai con xúc xắc nhỏ nhất là: 1 + 1 = 2 (chấm).
Hay tổng số chấm xuất hiện trên hai con xúc xắc luôn lớn hơn 1.
Vậy sự kiện “Tổng số chấm xuất hiện trên hai con xúc xắc luôn lớn hơn 1” chắc chắn xảy ra.
d) Hai mặt của con xúc xắc có cùng số chấm đều là: 1 chấm; 2 chấm; 3 chấm; 4 chấm; 5 chấm; 6 chấm.
Còn các trường hợp còn lại thì số chấm xuất hiện trên mỗi mặt của con xúc xắc sẽ khác nhau.
Vậy sự kiện “Hai mặt xuất hiện cùng số chấm” có thể xảy ra.