Giải Toán 6 Chân trời sáng tạo Bài 12: Ước chung, Ước chung lớn nhất
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 6 Bài 12: Ước chung, Ước chung lớn nhất sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 6 Bài 12. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài 12: Ước chung, Ước chung lớn nhất
Lời giải:
+ Trước khi học kiến thức Bài 12 này, ta sẽ giải quyết câu hỏi này bằng cách đi tìm tất cả các ước của 504 và 588, sau đó chọn ra các số giống nhau trong các ước của hai số trên, số lớn nhất trong các số đó là số cần tìm.
+ Sau bài này ta sẽ biết được cách làm đơn giản hơn như sau:
Cách làm như sau:
- Phân tích các số ra thừa số nguyên tố:
504 = 23.32.7
588 = 22.3.72
- Chọn các thừa số chung và số mũ nhỏ nhất của nó sau đó nhân lại ta được: 22.3.7 = 84
- Vậy số lớn nhất vừa là ước của 504 vừa là ước của 588 là 84.
Ta gọi 84 là ước chung lớn nhất của hai số 504 và 588.
Hoạt động khám phá 1 trang 36 Toán lớp 6 Tập 1:
b) Viết các tập hợp Ư(18), Ư(30). Liệt kê các phần tử chung của tập hợp này.
Lời giải:
a)
Để chia nhóm học sinh thành các nhóm khác nhau mà mỗi nhóm có số bạn nam bằng nhau, số bạn nữ bằng nhau thì số nhóm vừa phải là ước của 12, vừa phải là ước của 8.
Ta lấy 12 chia cho các số tự nhiên từ 1 đến 12, ta được Ư(12) = {1; 2; 3; 4; 6; 12}.
Ta lấy 8 chia cho các số tự nhiên từ 1 đến 8, ta được: Ư(8) = {1; 2; 4; 8}.
Vậy 12, 8 có cùng các ước là 1, 2, 4.
Do đó có 3 cách chia nhóm:
Cách 1: Chia 1 nhóm gồm 12 nam và 8 nữ.
Cách 2: Chia 2 nhóm, mỗi nhóm 6 nam, 4 nữ.
Cách 3: Chia 4 nhóm, mỗi nhóm 3 nam, 2 nữ.
b) Ta lấy 18 chia cho các số tự nhiên từ 1 đến 18 ta thấy 18 chia hết cho các số 1; 2; 3; 6; 9; 18.
Khi đó Ư(18) = {1; 2; 3; 6; 9; 18}.
Ta lấy 30 chia cho các số tự nhiên từ 1 đến 30 ta thấy 30 chia hết cho các số 1; 2; 3; 5; 6; 10; 15; 30.
Do đó Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}.
Các phần tử chung của hai tập hợp này là 1; 2; 3; 6.
Thực hành 1 trang 36 Toán lớp 6 Tập 1:
Các khẳng định sau đúng hay sai? Vì sao?
Lời giải:
a) Ta có: Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}
Các số 1; 2; 3; 6 vừa là ước của 24, vừa là ước của 30. Ta nói 1; 2; 3; 6 là các ước chung của 24 và 30, ta viết ƯC(24, 30) = {1; 2; 3; 6}
⇒ 6 ∈ ƯC(24, 30).
Vậy 6 ∈ ƯC(24, 30) là khẳng định đúng.
b) Ta có: Ư(28) = {1; 2; 4; 7; 14; 28}
Ư(42) = {1; 2; 3; 6; 7; 14; 21; 42}
Các số 1; 2; 7; 14 vừa là ước của 28, vừa là ước của 42. Ta nói 1; 2; 7; 14 là các ước chung của 28 và 42, ta viết ƯC(28, 42) = {1; 2; 7; 14}
⇒ 6 ∉ ƯC(28, 42).
Vậy 6 ∈ ƯC(28, 42) là khẳng định sai.
Ta có: Ư(18) = {1; 2; 3; 6; 9; 18}
Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ư(42) = {1; 2; 3; 6; 7; 14; 21; 42}
Các số 1; 2; 3; 6 vừa là ước của 18, vừa là ước của 24, vừa là ước của 42. Ta nói 1; 2; 3; 6 là các ước chung của 18, 24 và 42, ta viết ƯC(18, 24, 42) = {1; 2; 3; 6}
⇒ 6 ∈ ƯC(18, 24, 42).
Vậy 6 ∈ ƯC(18, 24, 42) là khẳng định đúng.
Thực hành 2 trang 37 Toán lớp 6 Tập 1:
Lời giải:
a) Ta có: Ư(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}
Ư(45) = {1; 3; 5; 9; 15; 45}
Do đó: ƯC(36, 45) = {1; 3; 9}.
b) Ta có: Ư(18) = {1; 2; 3; 6; 9; 18}
Ư(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}
Ư(45) = {1; 3; 5; 9; 15; 45}
Do đó: ƯC(18, 36, 45) = {1; 3; 9}.
Lời giải:
Số nam trong các đội bằng nhau và số nữ cũng bằng nhau, nên số đội nam (cũng là số đội nữ) là ước của 18 và 30, tức số đội là ước chung của 18 và 30.
Ư(18) = {1; 2; 3; 6; 9; 18}
Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}
ƯC(18; 30) = {1; 2; 3; 6}
Số đội được chia phải là vừa là ước của 18 vừa là ước của 30 nên số đội phải thuộc vào tập ƯC(18;30)
Hơn nữa số đội được chia phải nhiều nhất nên có thể chia chi đội đó thành 6 đội.
* Vậy: Có thể biểu diễn được nhiều nhất 6 tiết mục văn nghệ.
Thực hành 3 trang 37 Toán lớp 6 Tập 1: Viết ƯC(24, 30) và từ đó chỉ ra ƯCLN(24, 30).
Lời giải:
Ta có:
Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}
ƯC(24, 30) = {1; 2; 3; 6}
Trong các ước chung của 24 và 30, ta thấy 6 là ước lớn nhất
Do đó: ƯCLN(24, 30) = 6.
Vậy ƯCLN(24, 30) = 6.
Thực hành 4 trang 38 Toán lớp 6 Tập 1: Tìm ƯCLN(24, 60); ƯCLN(14, 33); ƯCLN(90,135, 270).
Lời giải:
+) Phân tích các số 24, 60 ra thừa số nguyên tố: 24 = 23.3; 60 = 22.3.5
Các thừa số nguyên tố chung là 2 và 3 với số mũ nhỏ nhất lần lượt là 2 và 1.
Vậy ƯCLN(24, 60) = 22.3 = 12
+) Phân tích các số 14 và 33 ra thừa số nguyên tố: 14 = 2.7, 33 = 33
Vậy ƯCLN(14, 33) = 1
+) Phân tích: 90 = 2.32.5; 135 = 33.5; 270 = 2.33.5
Các thừa số nguyên tố chung là 3 và 5 với số mũ nhỏ nhất lần lượt là 2 và 1
Vậy ƯCLN(90,135, 270) = 32.5 = 45.
Thực hành 5 trang 38 Toán lớp 6 Tập 1:
.Lời giải:
Để rút gọn một phân số, ta có thể chia cả tử và mẫu của phân số đó cho ước chung lớn nhất của chúng để được phân số tối giản.
+) Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ư(108) = {1; 2; 3; 4; 6; 9; 12; 18; 27; 36; 54; 108}
ƯCLN(24; 108) = 12
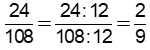
+) Ư(80) = {1; 2; 4; 5; 8; 10; 16; 20; 40; 80}
Ư(32) = {1; 2; 4; 8; 16; 32}
ƯCLN(80; 32) = 16
Bài 1 trang 38 Toán lớp 6 Tập 1:
a) ƯC(12, 24) = {1; 2; 3; 4; 6; 8; 12};
b) ƯC(36, 12, 48) = {1; 2; 3; 4; 6; 12}.
Lời giải:
a) Khẳng định a là sai vì:
Ư(12) = {1; 2; 3; 4; 6; 12}
Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Suy ra ƯC(12, 24) = {1; 2; 3; 4; 6; 12}
Do đó 8 không phải là phần tử của tập ƯC(12, 24).
b) Khẳng định b là đúng vì:
Ta có:
Ư(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}
Ư(12) = {1; 2; 3; 4; 6; 12}
Ư(48) = {1; 2; 3; 4; 6; 8; 12; 16; 24; 48}
Suy ra ƯC(36, 12, 48) = {1; 2; 3; 4; 6; 12}.
Bài 2 trang 39 Toán lớp 6 Tập 1:
a) ƯCLN(1, 16); b) ƯCLN(8, 20);
c) ƯCLN(84, 156); c) ƯCLN(16, 40, 176).
Lời giải:
a) ƯCLN(1, 16) = 1.
b) Phân tích 8 và 30 ra thừa số nguyên tố: 8 = 23; 20 = 22.5.
Các thừa số nguyên tố chung là 2.
Lập tích các thừa số chung vừa chọn được, mỗi thừa số lấy với số mũ nhỏ nhất của nó là: 22.
Vậy ƯCLN(8, 20) = 22 = 4.
c) Phân tích 84 và 156 ra thừa số nguyên tố: 84 = 22.3.7; 156 = 22.3.13.
Các thừa số nguyên tố chung là 2 và 3.
Lập tích các thừa số chung vừa chọn được, mỗi thừa số lấy với số mũ nhỏ nhất của nó là: 22.3.
Vậy ƯCLN(84, 156) = 22.3 = 12.
d) Phân tích 16, 40 và 176 ra thừa số nguyên tố: 16 = 24; 4- = 23.5; 176 = 24.11.
Các thừa số nguyên tố chung là 2.
Lập tích các thừa số chung vừa chọn được, mỗi thừa số lấy với số mũ nhỏ nhất của nó là: 23.
Vậy ƯCLN(16, 40, 176) = 23 = 8.
Bài 3 trang 39 Toán lớp 6 Tập 1:
i. 24 và 30; ii. 42 và 98; iii. 180 và 234.
Lời giải:
a) Các ước của 6 là 1, 2, 3, 6.
Do đó ta có tập hợp A = Ư(6) = {1; 2; 3; 6}.
Ư(18) = {1; 2; 3; 6; 9; 18}.
Ư(30) = {1; 2; 3; 5; 6; 10; 15; 30}.
ƯC(18, 30) = {1; 2; 3; 6}.
Nhận xét: Ta thấy tập hợp ƯC(18, 30) = {1; 2; 3; 6} nên tập hợp ƯC (18, 30) giống với tập hợp A.
Tổng quát: Cho hai số tự nhiên a và b. Để tìm tập ƯC(a,b) ta sẽ tìm ƯCLN(a, b) = m. Khi đó ƯC(a, b) = Ư(m).
b)
i. Phân tích 24 và 30 ra thừa số nguyên tố: 24 = 23.3; 30 = 2.3.5.
Suy ra ƯCLN(24, 30) = 2.3 =6.
Vậy: ƯC(24, 30) = Ư(6) = {1; 2; 3; 6}.
ii. Ta phân tích các số 42 và 98 ra thừa số nguyên tố
42 = 2.3.7; 98 = 2.72
Suy ra ƯCLN(42, 98) = 2.7 = 14.
Vậy: ƯC (42, 98) = Ư(14) = {1; 2; 7; 14}.
iii.Ta phân tích các số 180 và 234 ra thừa số nguyên tố
180 = 22.5.32; 234 = 2.32.13
Suy ra ƯCLN(180, 234) = 2.32 = 18
Vậy: ƯC(180, 234) = Ư(18) = {1; 2; 3; 6; 9; 18}.
Bài 4 trang 39 Toán lớp 6 Tập 1:
.Lời giải:
Để rút gọn một phân số, ta chia cả tử và mẫu của phân số cho ƯCLN của chúng để được phân số tối giản.
+) Ta có: 28 = 22.7; 42 = 2.3.7.
Suy ra ƯCLN(28, 42) = 14
+) Ta có: 60 = 22.3.5; 135 = 33.5.
Suy ra ƯCLN(60, 135) = 15
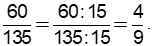
+) Ta có: 288 = 25.32; 180 = 22.32.5
ƯCLN(288, 180) = 36
Lời giải:
Bởi vì chị Lan muốn cắt cả ba đoạn dây đó thành những đoạn ngắn hơn có cùng chiều dài.
Nên độ dài lớn nhất có thể của mỗi đoạn dây ngắn được cắt ra chính là ước chung lớn nhất của 140, 168 và 210.
Ta tìm ước chung lớn nhất của 140, 168, 210:
Ta có: 140 = 22.5.7
168 = 23.3.7
210 = 2.3.5.7
Suy ra ƯCLN(140, 168, 210) = 2 . 7 = 14.
Độ dài lớn nhất có thể của mỗi đoạn dây ngắn được cắt ra là: 14 cm.
- Mỗi đoạn dây khác nhau có thể cắt được số đoạn dây ngắn là:
Đoạn dây dài 140 cm cắt được: 140 : 14 = 10 (đoạn).
Đoạn dây dài 168 cm cắt được: 168 : 14 = 12 (đoạn).
Đoạn dây dài 210 cm cắt được: 210 : 14 = 15 (đoạn).
- Số đoạn dây ruy băng ngắn chị Lan có được là:
10 + 12 + 15 = 37 (đoạn dây).
Kết luận: Chị Lan có được tổng cộng 37 đoạn dây ruy băng ngắn sau khi cắt với độ dài mỗi đoạn là 14 cm.
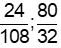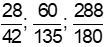Bài viết liên quan
- Giải Toán 6 Chân trời sáng tạo Bài 10: Số nguyên tố, Hợp số, Phân tích một số ra thừa số nguyên tố
- Giải Toán 6 Chân trời sáng tạo Bài 11: Hoạt động thực hành và trải nghiệm
- Giải Toán 6 Chân trời sáng tạo Bài 13: Bội chung, Bội chung nhỏ nhất
- Giải Toán 6 Chân trời sáng tạo Bài 14: Hoạt động thực hành và trải nghiệm
- Giải Toán 6 Chân trời sáng tạo Bài tập cuối chương 1
