Giải Toán 6 Chân trời sáng tạo Bài tập cuối chương 3
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 6 Bài tập cuối chương 3 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 6 Bài tập cuối chương 3. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài tập cuối chương 3
Câu 1 trang 93 Toán lớp 6 Tập 1:
Hình thoi có độ dài hai đường chéo lần lượt là 50 m và 60 m thì diện tích là:
Lời giải:
Diện tích hình thoi đã cho là: 50.60:2 = 1500 m2
Chọn C.
Câu 2 trang 93 Toán lớp 6 Tập 1:
Hình thang cân có độ dài cạnh đáy và chiều cao lần lượt là 40 m, 30 m, 25 m, có diện tích là:
Lời giải:
Diện tích hình thang cân là: (40 + 30 ).25:2 = 875 m2
Chọn C.
Câu 3 trang 93 Toán lớp 6 Tập 1:
Lời giải:
Diện tích hình bình hành là: 70.50 (dm2).
Đổi 3500 dm2 = 35m2
Chọn A.
Bài 1 trang 93 Toán lớp 6 Tập 1:
a) Tam giác đều có cạnh là 5 cm.
b) Hình chữ nhật có chiều dài 5 cm và chiều rộng 3 cm.
d) Hình bình hành có hai cạnh liên tiếp là 6 cm, 8 cm và chiều cao bằng 4 cm.
e) Hình thoi có cạnh dài 5 cm.
Lời giải:
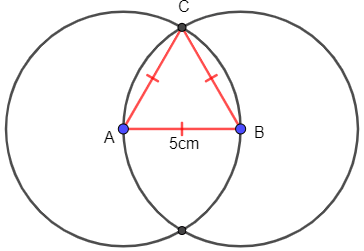
a) Tam giác đều có cạnh là 5 cm
- Vẽ đoạn thẳng AB = 5 cm.
- Vẽ đường tròn tâm A, bán kính 5 cm; vẽ đường tròn tâm B bán kính 5 cm.
- Hai đường tròn cắt nhau ở C, ta được tam giác đều ABC cạnh 5 cm.
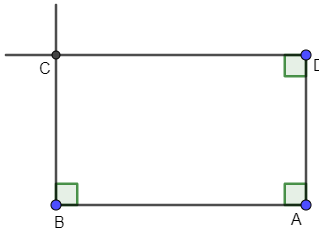
b) Hình chữ nhật có chiều dài 5 cm và chiều rộng 3 cm.
- Vẽ đoạn thẳng AB = 5 cm, AD = 3 cm sao cho AB vuông góc với AD.
- Vẽ đường thẳng vuông góc với AB tại B và đường thẳng vuông góc với AD tại D.
- Hai đường thẳng này cắt nhau tại C ta được hình chữ nhật ABCD thỏa mãn yêu cầu.
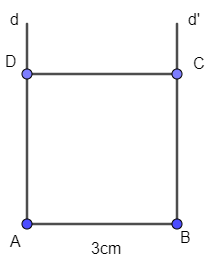
c) Hình vuông có cạnh 3 cm.
- Vẽ đoạn thẳng AB = 3 cm.
- Vẽ hai đường thẳng d, d’ lần lượt vuông góc với AB tại A và B.
- Trên đường thẳng d lấy điểm D, trên đường thẳng d’ lấy điểm C sao cho AD = BC = 3 cm.
- Nối C với D ta được hình vuông ABCD có cạnh 3 cm.
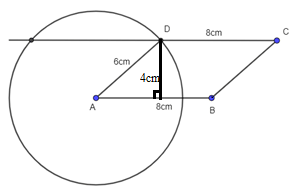
d) Hình bình hành có hai cạnh liên tiếp là 6 cm, 8 cm và chiều cao bằng 4 cm.
- Vẽ đoạn thẳng AB = 8 cm.
- Vẽ đường thẳng d song song với AB cách AB một khoảng bằng 4 cm.
- Vẽ đường tròn tâm A bán kính 6 cm. Đường tròn này cắt đường thẳng d tại điểm D.
- Trên đường thẳng d lấy đoạn thẳng DC = 8 cm.
- Nối C với B ta được hình bình hành ABCD thỏa mãn yêu cầu bài toán.
e) Hình thoi có cạnh dài 5 cm.
- Vẽ đoạn thẳng AB = 5cm.
- Vẽ đường tròn tâm A bán kính 5 cm. Trên đường tròn này lấy điểm D.
- Từ D vẽ đường thẳng song song với AB. Trên đường thẳng này lấy điểm C sao cho DC = 5 cm.
- Nối C với B ta được hình thoi ABCD có cạnh 5 cm.
Bài 2 trang 93 Toán lớp 6 Tập 1: Hãy cắt 3 hình như hình dưới đây và ghép lại để được một hình vuông
Lời giải:
Sau khi cắt ta ghép lại thành hình vuông như sau:
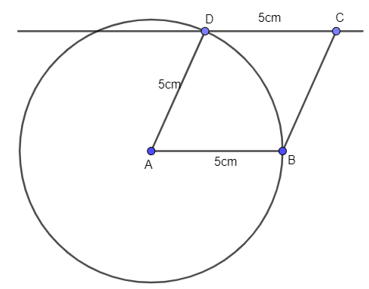
Bài 3 trang 93 Toán lớp 6 Tập 1: Hình đưới đây gồm các hình nào?
Lời giải:
Hình đã cho gồm các hình: Hình tam giác đều, hình thoi, hình thang cân và hình lục giác đều được xác định như sau:
- Hình tam giác đều
- Hình thoi
- Hình thang cân
- Hình lục giác đều
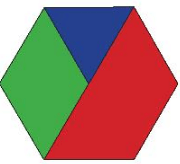
Lời giải:
Từ 5 hình bình hành, ta sẽ ghép như hình dưới đây để tạo thành một hình bình hành.
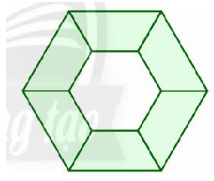
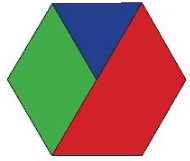
Lời giải:
Hình vẽ trên có tất cả 6 hình thang cân và 2 hình lục giác đều.
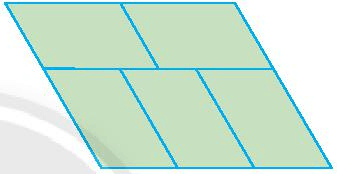
Bài 6 trang 93 Toán lớp 6 Tập 1: Hãy cắt 6 hình tam giác đều rồi ghép lại thành hình bình hành.
Lời giải:
Cắt 6 hình tam giác đều và ghép lại như hình vẽ dưới đây ta được hình bình hành:
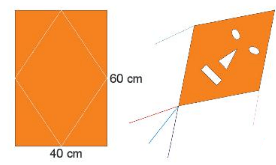
Lời giải:
Chiều dài và chiều rộng của hình chữ nhật chính là độ dài của hai đường chéo của hình thoi nên diện tích của con diều hình thoi là:
60.40:2 = 1200 ( cm2 )
Vậy diện tích con diều là 1200cm2.
Giải Toán 6 Chân trời sáng tạo Bài 1: Thu thập và phân loại dữ liệu
Giải Toán 6 Chân trời sáng tạo Bài 2: Biểu diễn dữ liệu trên bảng
Giải Toán 6 Chân trời sáng tạo Bài 3: Biểu đồ tranh
Giải Toán 6 Chân trời sáng tạo Bài 4: Biểu đồ cột - Biểu đồ cột kép
Giải Toán 6 Chân trời sáng tạo Bài 5: Hoạt động thực hành và trải nghiệm
Bài viết liên quan
- Giải Toán 6 Chân trời sáng tạo Bài 1: Hình vuông - Tam giác đều - Lục giác đều
- Giải Toán 6 Chân trời sáng tạo Bài 2: Hình chữ nhật - Hình thoi - Hình bình hành - Hình thang cân
- Giải Toán 6 Chân trời sáng tạo Bài 3: Chu vi và diện tích của một số hình trong thực tiễn
- Giải Toán 6 Chân trời sáng tạo Bài 4: Hoạt động thực hành và trải nghiệm: Tính chu vi và diện tích của một số hình trong thực tiễn
