Giải Toán 6 Chân trời sáng tạo Bài 1: Hình có trục đối xứng
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 6 Bài 1: Hình có trục đối xứng sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 6 Bài 1. Mời các bạn đón xem:
Giải bài tập Toán 6 Bài 1: Hình có trục đối xứng
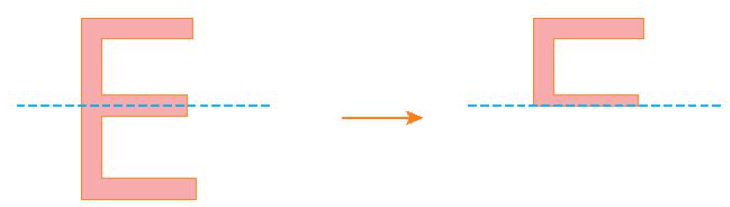
Em có nhận xét gì về hai nửa của mỗi hình bên trái.
Lời giải:
Hình a:
Ta ghép hai hình bên phải theo đường nét đứt, ta được hình bên trái (như hình vẽ)
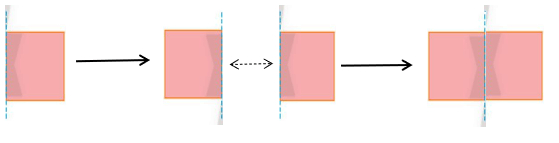
Nhận xét: Hai nửa hình bên trái bằng nhau và đều bằng hình bên phải.
Hình b:
Ta ghép hai hình bên phải theo đường nét đứt, ta được hình bên trái (như hình vẽ)
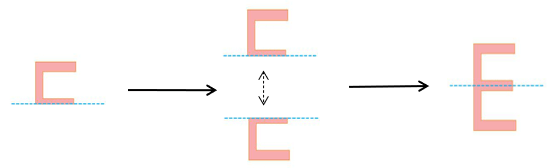
Nhận xét: Hai nửa hình bên trái bằng nhau và đều bằng hình bên phải.
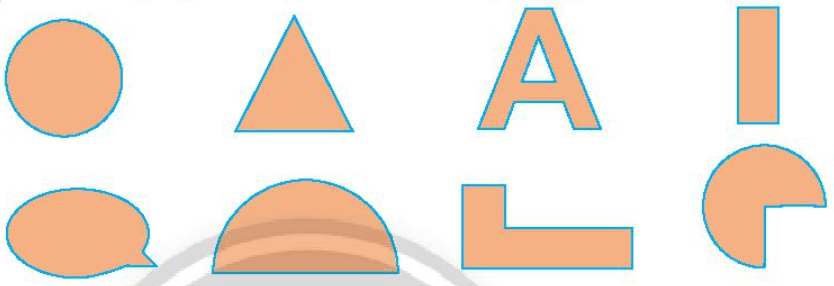
Thực hành 1 trang 53 Toán lớp 6 Tập 2: Tìm một trục đối xứng của các hình sau (nếu có).
Lời giải:
Hình có trục đối xứng là hình tồn tại một đường thẳng chia hình thành 2 phần sao cho hai phần của hình chồng khít lên nhau. Đường thẳng đó là trục đối xứng của hình.
Một trục đối xứng của các hình được biểu diễn trên hình vẽ như sau:
Hình thứ nhất:
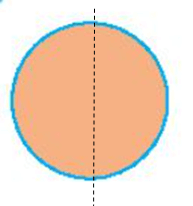
Hình thứ hai:
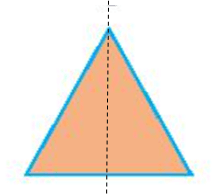
Hình thứ ba:
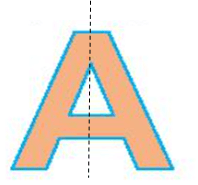
Hình thứ tư:
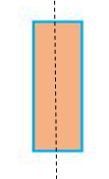
Hình thứ năm: Không có trục đối xứng.
Hình thứ sáu:
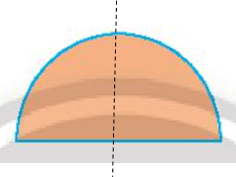
Hình thứ bảy: Không có trục đối xứng.
Hình thứ tám:
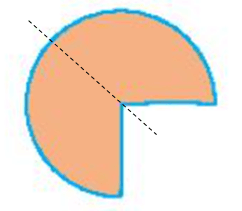
Vận dụng trang 53 Toán lớp 6 Tập 2:
Mỗi hình sau có bao nhiêu trục đối xứng:
Lời giải:
Trục đối xứng của mỗi hình được biểu diễn như sau:
- Hình a) có hai trục đối xứng (như hình vẽ).
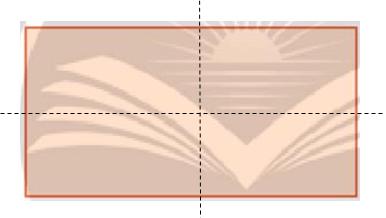
- Hình b) có hai trục đối xứng (như hình vẽ).
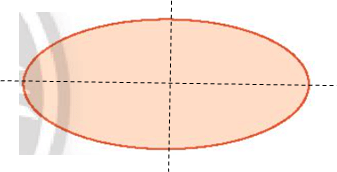
- Hình c) có ba trục đối xứng (như hình vẽ).
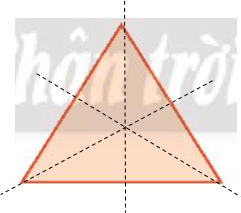
- Hình d) có bốn trục đối xứng (như hình vẽ).
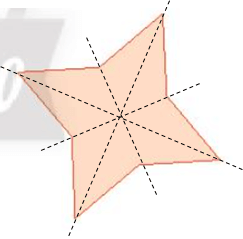
Lời giải:
Hình thứ nhất có trục đối xứng (như hình vẽ).

Hình thứ hai không có trục đối xứng.
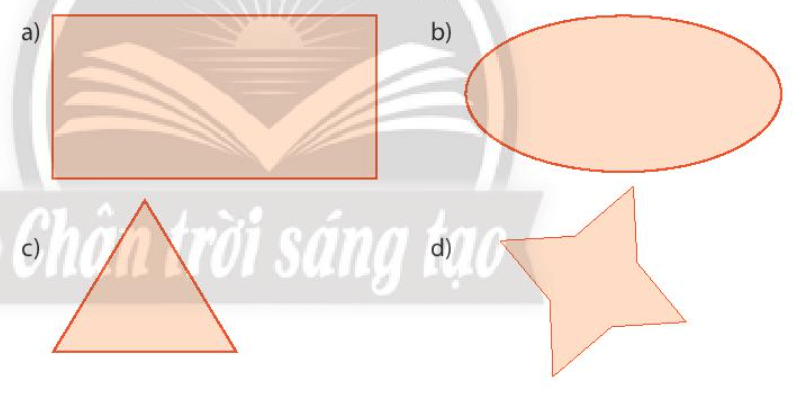
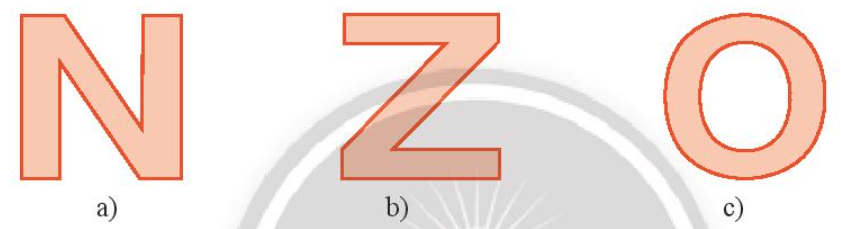
Bài 1 trang 54 Toán lớp 6 Tập 2: Hình nào sau đây có trục đối xứng?
Lời giải:
Hình a) không có trục đối xứng.
Hình b) có trục đối xứng (như hình vẽ).
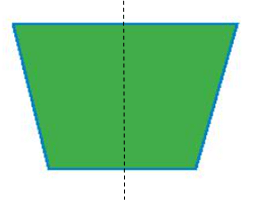
Hình c) có trục đối xứng (như hình vẽ).
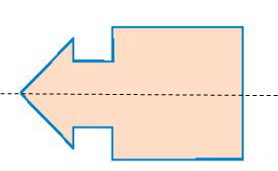
Hình d) có trục đối xứng (như hình vẽ).
Vậy những hình có trục đối xứng là hình b), hình c) và hình d).
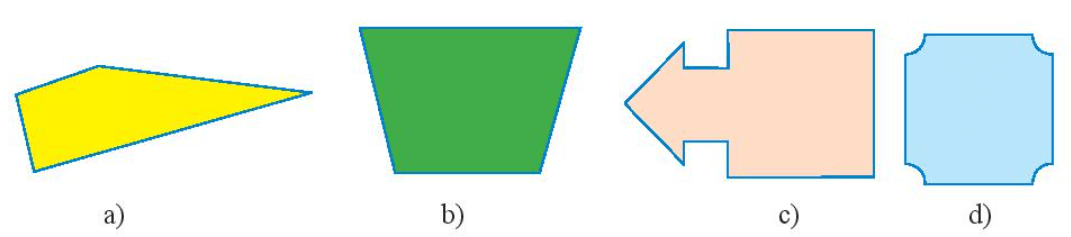
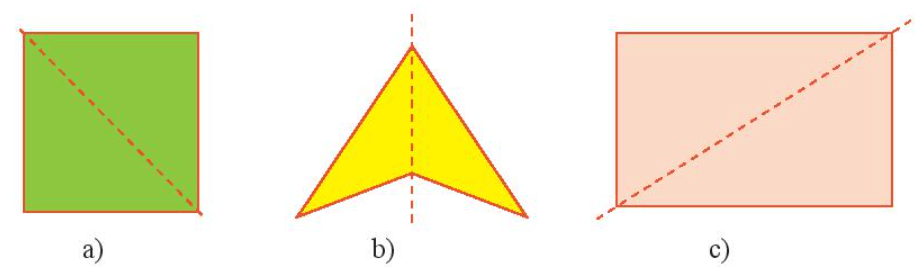
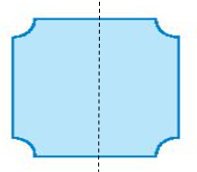
Bài 2 trang 55 Toán lớp 6 Tập 2: Đường nét đứt có phải là trục đối xứng của mỗi hình sau không?
Lời giải:
- Hình a) gập đôi hình theo đường nét đứt, ta được hai nửa hình chồng khít lên nhau nên đường nét đứt là trục đối xứng.
- Hình b) gập đôi hình theo đường nét đứt, ta được hai nửa hình chồng khít lên nhau nên đường nét đứt là trục đối xứng.
- Hình c) gập đôi hình theo đường nét đứt, ta được hai nửa hình không chồng khít lên nhau nên đường nét đứt không phải là trục đối xứng.
Vậy hình a) và hình c) có đường nét đứt là trục đối xứng của hình.
Bài 3 trang 55 Toán lớp 6 Tập 2: Tìm trục đối xứng của mỗi hình sau.
Lời giải:
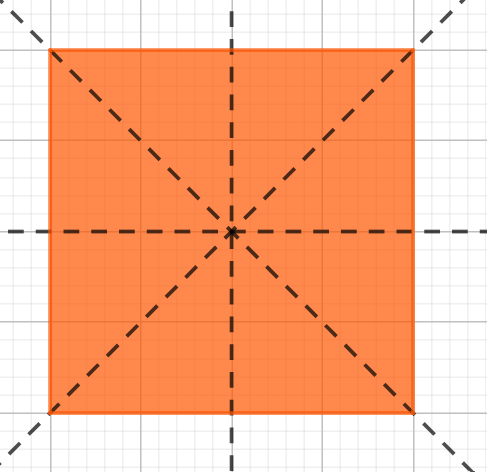
a) Hình vuông có bốn trục đối xứng gồm:
- Hai đường chéo của hình vuông.
- Hai đường thẳng đi qua giao điểm của hai đường chéo và vuông góc với hai trong bốn cạnh của hình vuông.
Hình minh họa:
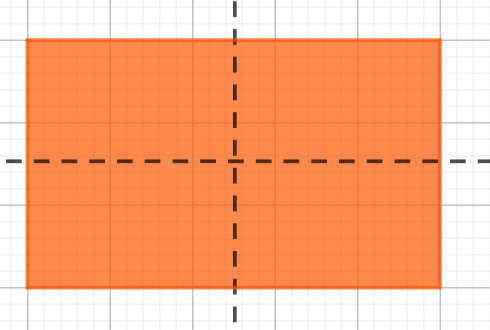
b) Hình chữ nhật có hai trục đối xứng là đường thẳng đi qua trung điểm của các cặp cạnh đối diện của hình chữ nhật.
Hình minh họa:
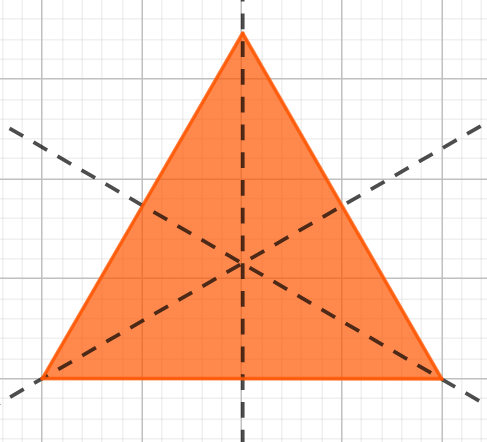
c) Hình tam giác đều có ba trục đối xứng là ba đường cao của tam giác.
Hình minh họa:
d) Hình bình hành không có trục đối xứng.
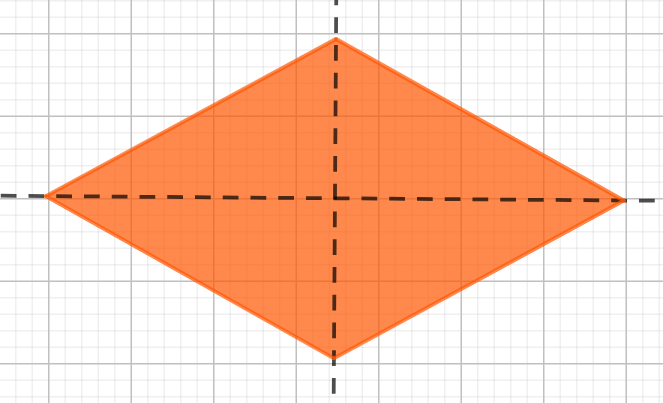
e) Hình thoi có hai trục đối xứng là hai đường chéo.
Hình minh họa:
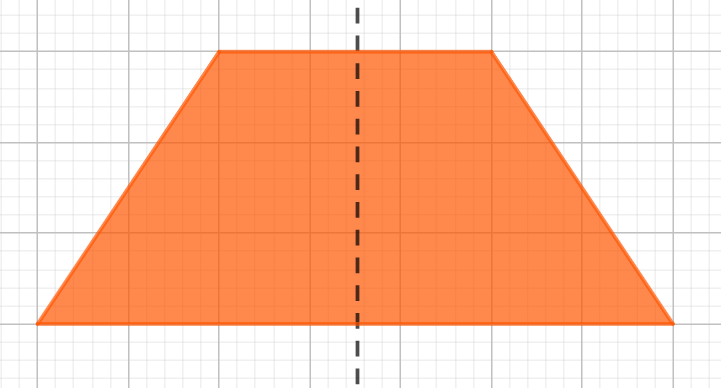
g) Hình thang cân có một trục đối xứng là đường thẳng đi qua trung điểm hai đáy.
Hình minh họa:
Lời giải:
Hình a) không có trục đối xứng.
Hình b) không có trục đối xứng.
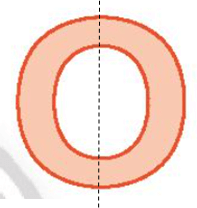
Hình c) có trục đối xứng, được biểu diễn như trên hình vẽ.
Bài 5 trang 55 Toán lớp 6 Tập 2: Hình con cua và hình củ khoai bên dưới, hình nào có trục đối xứng?
Lời giải:
Hình con cua có trục đối xứng, được biểu diễn như hình vẽ.

Hình củ khoai lang không có trục đối xứng.
Vậy hình con cua và hình củ khoai lang, chỉ có hình con cua có trục đối xứng.