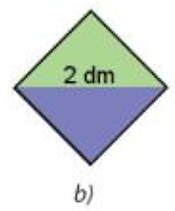
Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông (H.2.2b)
Lời giải HĐ 2 trang 29 Toán 7 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7 Tập 1.
Giải Toán 7 Bài 6: Số vô tỉ. Căn bậc hai số học
HĐ 2 trang 29 Toán 7 Tập 1: Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông (H.2.2b). Em hãy tính diện tích hình vuông nhận được.
Lời giải:
Từ bốn tam giác vuông nhận được theo cách cắt ở hoạt động 1 ta ghép tam giác 2 và tam giác 4 với nhau để được hình vuông như hình vẽ dưới đây:
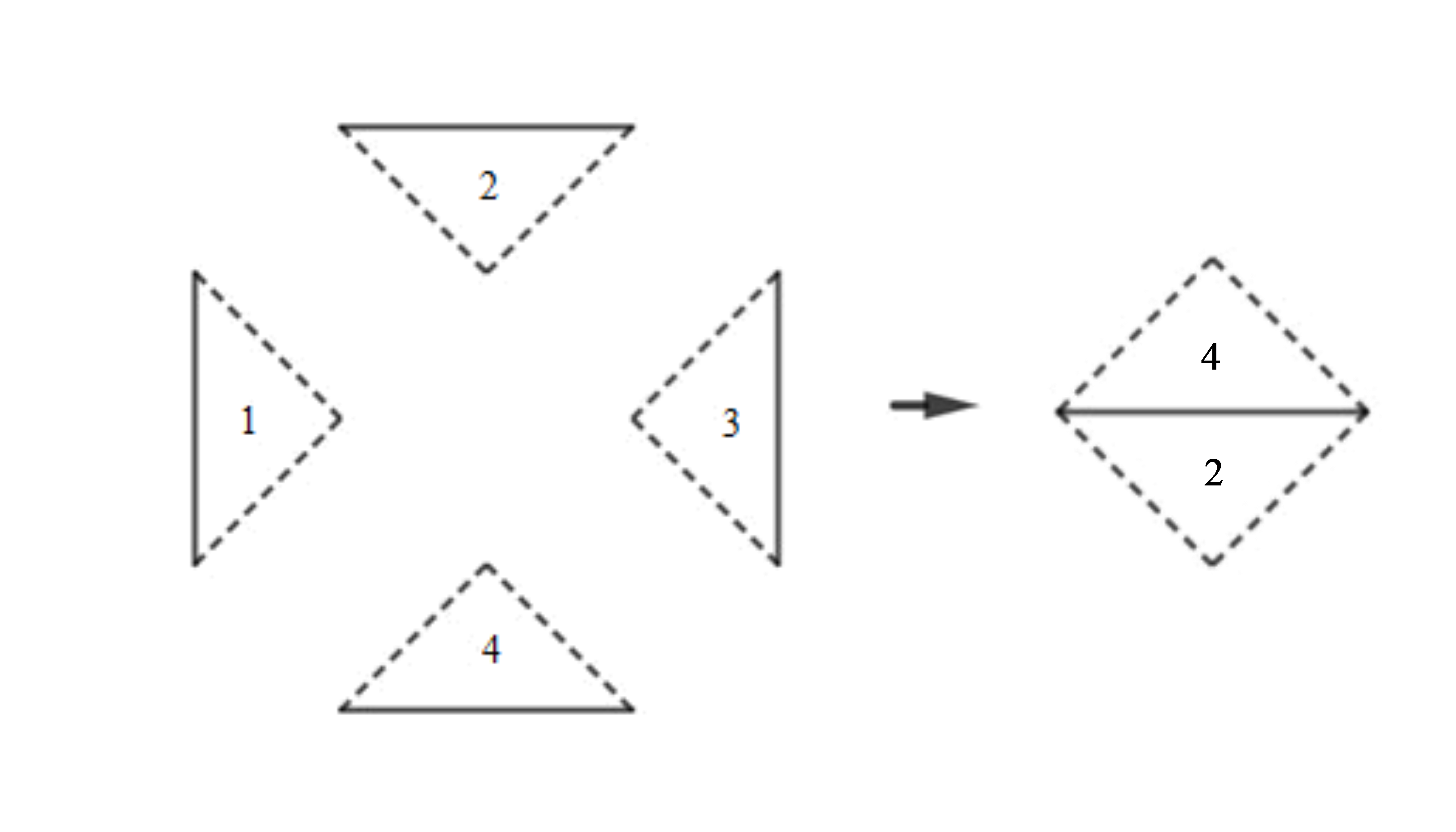
Diện tích của hình vuông lớn ban đầu có cạnh 2 dm là: 2.2 = 4 (dm2).
Sau khi chia hình vuông đó thành 4 tam giác vuông bằng nhau thì diện tích của mỗi tam giác vuông đó là: 4 : 4 = 1 (dm2).
Ghép 2 trong 4 tam giác bằng nhau (như hình vẽ ghép tam giác 2 và tam giác 4 với nhau) để được một hình vuông thì hình vuông này có diện tích bằng 2 lần diện tích của một tam giác vuông.
Do đó diện tích hình vuông nhận được sau khi ghép là: 2.1 = 2 (dm2).
Vậy diện tích hình vuông nhận được sau khi ghép hai tam giác vuông bằng nhau trong hoạt động 1 là: 2 dm2.
Xem thêm lời giải bài tập Toán 7 Tập 1 Kết nối tri thức hay, chi tiết khác:
HĐ 2 trang 29 Toán 7 Tập 1: Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông (H.2.2b)
HĐ 3 trang 29 Toán 7 Tập 1: Dùng thước có vạch chia để đo độ dài cạnh hình vuông nhận được trong HĐ2
Vận dụng 1 trang 30 Toán 7 Tập 1: Người xưa đã tính đường kính thân cây theo quy tắc “quân bát, phát tam, tồn ngũ, quân nhị”
Vận dụng 2 trang 30 Toán 7 Tập 1: Sàn thi đấu bộ môn cử tạ có dạng một hình vuông, diện tích 144 m2. Em hãy tính chu vi của sàn thi đấu đó
Bài 2.8 trang 32 Toán 7 Tập 1: Khi tìm căn bậc hai số học của một số tự nhiên ta thường phân tích số đó ra thừa số nguyên tố
Bài 2.9 trang 32 Toán 7 Tập 1: Tính độ dài cạnh của hình vuông có diện tích bằng: a) 81 dm^2; b) 3 600 m^2; c) 1 ha
Bài 2.10 trang 32 Toán 7 Tập 1: Sử dụng máy tính cầm tay tìm căn bậc hai số học của các số sau rồi làm tròn các kết quả với độ chính xác 0,005. a) 3; b) 41; c) 2 021


