Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý

Lời giải Bài 1 trang 97 Toán lớp 10 Tập 1 Toán 10 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán lớp 10 Tập 1.

573

« Trang trước

Trang sau »

Giải Toán lớp 10 Bài 3: Tích của một số với một vectơ

Bài 1 trang 97 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:

a) $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$ ;

b) $\vec{A B} + \vec{A C} + \vec{A D} = 2 \vec{A C}$ .

Lời giải:

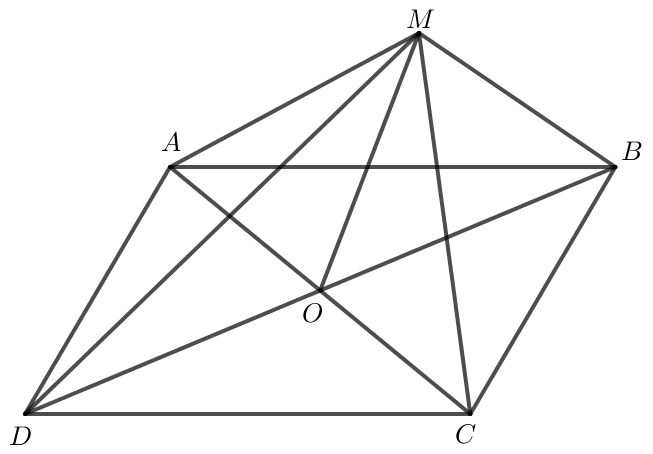
Giải Toán 10 Bài 3: Tích của một số với một vectơ - Chân trời sáng tạo (ảnh 1)

a) Hình bình hành ABCD có O là giao điểm hai đường chéo nên OA = OC, OB = OD.

Khi đó $\vec{O A}$ và $\vec{O C}$ là hai vectơ đối, $\vec{O B}$ và $\vec{O D}$ là hai vectơ đối.

Do đó $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{0}$ .

Ta có $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = \vec{M O} + \vec{O A} + \vec{M O} + \vec{O B} + \vec{M O} + \vec{O C} + \vec{M O} + \vec{O D}$

$= 4 \vec{M O} + (\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D})$

$= 4 \vec{M O}$

Vậy $\vec{M A} + \vec{M B} + \vec{M C} + \vec{M D} = 4 \vec{M O}$

b) Áp dụng quy tắc hình bình hành ta có $\vec{A B} + \vec{A D} = \vec{A C}$ .

Do đó $\vec{A B} + \vec{A D} + \vec{A C} = \vec{A C} + \vec{A C}$ hay $\vec{A B} + \vec{A C} + \vec{A D} = 2 \vec{A C}$ .

Vậy $\vec{A B} + \vec{A C} + \vec{A D} = 2 \vec{A C}$ .

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 1 trang 97 Toán lớp 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý

Bài 3 trang 97 Toán lớp 10 Tập 1: Cho hai điểm phân biệt A và B. Xác định điểm M sao cho:

\vec{M A}

+ 4

\vec{M B}

\vec{0}

Bài 4 trang 97 Toán lớp 10 Tập 1: Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF

Bài 5 trang 97 Toán lớp 10 Tập 1: Máy bay A đang bay về hướng đông bắc với tốc độ 600 km/h

Bài 6 trang 97 Toán lớp 10 Tập 1: Cho hai điểm phân biệt A và B. Xác định điểm O sao cho

\vec{O A}

+ 3

\vec{O B}

\vec{0}

573

« Trang trước

Trang sau »

Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý

Có thể bạn quan tâm