Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo và AB = a, BC = 3a
Lời giải Bài 2 trang 102 Toán lớp 10 Tập 1 Toán 10 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán lớp 10 Tập 1.
Giải Toán lớp 10 Bài tập cuối chương 5
Bài 2 trang 102 Toán lớp 10 Tập 1: Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo và AB = a, BC = 3a.
a) Tính độ dài của các vectơ .
b) Tìm trong hình các cặp vectơ đối nhau và có độ dài bằng .
Lời giải:
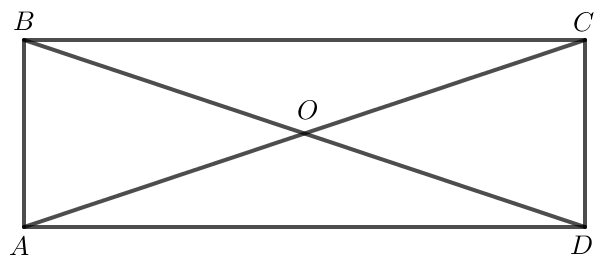
a) Áp dụng định lí Pythagore vào tam giác ABC vuông tại B:
AC2 = AB2 + BC2
AC2 = a2 + (3a)2
AC2 = 10a2
AC = a (do AC là độ dài đoạn thẳng nên AC > 0)
Do ABCD là hình chữ nhật nên AC = BD = a.
Vậy .
b) Ta thấy = .
Do đó độ dài các vectơ đó bằng độ dài của AC và BD.
Vậy các cặp vectơ đối nhau và có độ dài bằng là: và ; và ; và ; và .
Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:


