Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý
Lời giải Bài 10 trang 103 Toán lớp 10 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán lớp 10 Tập 1.
Giải Toán lớp 10 Bài tập cuối chương 5
Bài 10 trang 103 Toán lớp 10 Tập 1: Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng .
Lời giải:
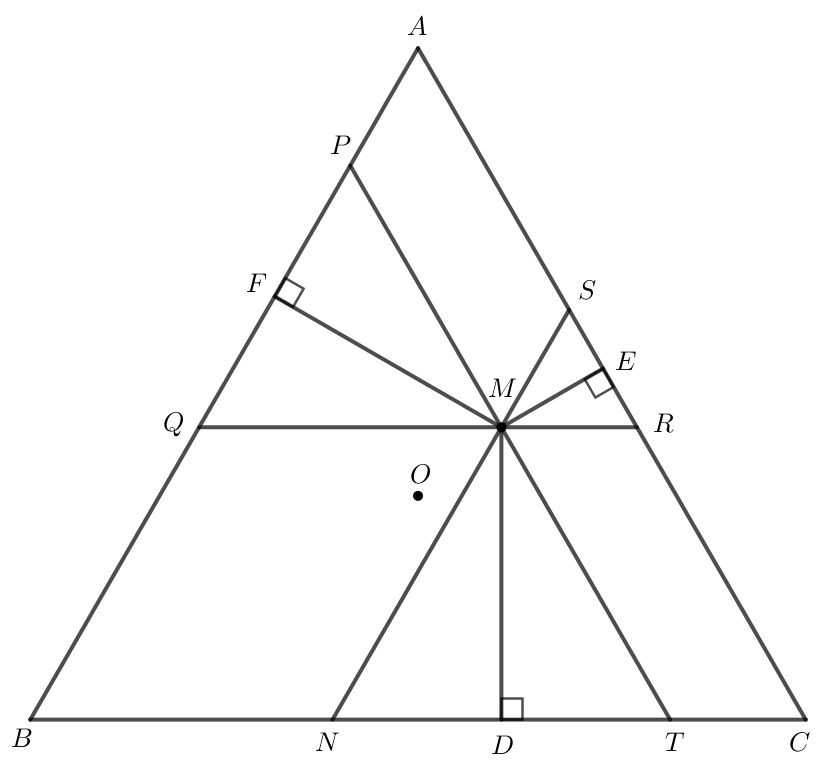
Tam giác ABC đều nên .
Qua M kẻ NS // AB, PT // AC, RQ // BC.
Do NS //AB nên và .
Do PT // AC nên và .
Do RQ // BC nên và .
Khi đó các tam giác MNT, MRS và MPQ là các tam giác đều.
Tam giác MNT đều có MD NT nên D là trung điểm của NT.
Tam giác MRS đều có ME RS nên E là trung điểm của RS.
Tam giác MPQ đều có MF PQ nên F là trung điểm của PQ.
Do D là trung điểm của NT nên .
Do E là trung điểm của RS nên .
Do F là trung điểm của PQ nên .
Do đó
Tứ giác MNBQ có MN // BQ và MQ // BN nên MNBQ là hình bình hành.
Tứ giác MTCR có MT // CR và MR // CT nên MTCR là hình bình hành.
Tứ giác MSAP có MP // AS và MS // AP nên MSAP là hình bình hành.
Khi đó áp dụng quy tắc hình bình hành ta có:
; ; .
Do đó .
Do O là trọng tâm của tam giác ABC nên hay
.
Do đó .
Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài viết liên quan
- Giải Toán 10 (Chân trời sáng tạo) Bài 1: Khái niệm vectơ
- Giải Toán 10 (Chân trời sáng tạo) Bài 2: Tổng và hiệu của hai vectơ
- Giải Toán 10 (Chân trời sáng tạo) Bài 3: Tích của một số với một vectơ
- Giải Toán 10 (Chân trời sáng tạo) Bài 4: Tích vô hướng của hai vectơ
- Giải Toán 10 (Chân trời sáng tạo) Bài tập cuối chương 5
