Giải Toán lớp 10 Bài tập cuối chương 2

Bài 1 trang 39 Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ Oxy.

a) -2x + y - 1 ≤ 0;

b) -x + 2y > 0;

c) x – 5y < 2

d) -3x + y + 2 ≤ 0;

e) 3(x – 1) + 4(y – 2 ) < 5x – 3.

Lời giải:

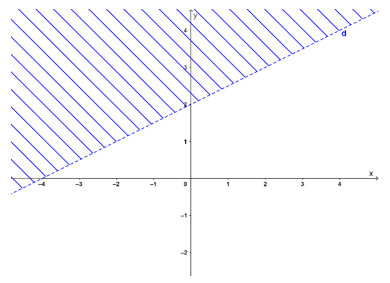
a) –2x + y – 1 ≤ 0           

Vẽ đường thẳng d: –2x + y – 1 =  0 qua hai điểm (0; 1) và (–1; –1)

Xét gốc toạ độ O(0; 0) ta thấy: O ∉ d và –2.0 + 0 – 1 = –1 < 0 . Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O (không kể bờ d) (miền không gạch chéo).

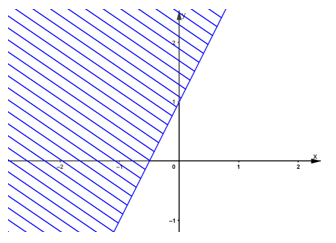
b) –x + 2y > 0

Vẽ đường thẳng d: –x + 2y = 0 đi qua hai điểm (0; 0) và (2; 1)

Xét điểm A(1; 1) ta thấy: A ∉ d và –1 + 2.1 = 1 > 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm A (không kể bờ d) (miền không gạch chéo).

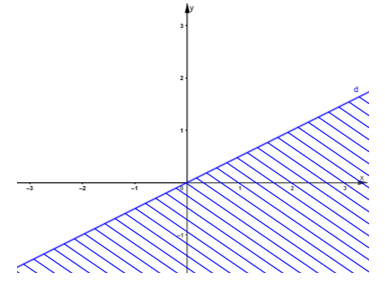
c) x – 5y < 2 ⇔ x – 5y – 2 < 0 

Vẽ đường thẳng d: x – 5y – 2 = 0  qua hai điểm (2; 0) và (7; 1).

Xét điểm O(0; 0) ta thấy: O ∉ d và 0 – 5.0 – 2 = -2  < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O (không kể bờ d) (miền không gạch chéo).

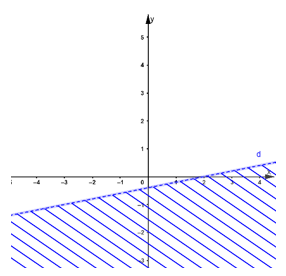
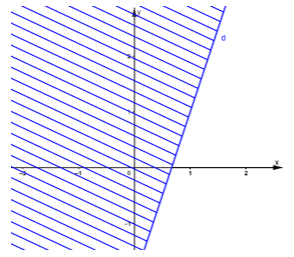
d) –3x + y + 2 ≤ 0

Vẽ đường thẳng d: –3x + y + 2 = 0 qua hai điểm (0; - 2); (1; 1).

Xét điểm O(0; 0) ta thấy: O ∉ d và –3.0 + 0 + 2 = 2 > 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không chứa điểm O (không kể bờ d) (miền không gạch chéo).

e) 3(x – 1) + 4. ( y – 2)  < 5x – 3

⇔ 3x – 3 +4y – 8 – 5x + 3 < 0

⇔ – 2x + 4y – 8 < 0

⇔ – x + 2y – 4 < 0

Vẽ đường thẳng d: – x + 2y – 4 = 0 qua hai điểm (0;  2) và (-2; 1)

Xét điểm O(0; 0) ta thấy: O ∉ d và –0 + 2.0 – 4 = –4 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O (không kể bờ d) (miền không gạch chéo).