Giải Toán lớp 10 Bài tập cuối chương 2

Bài 4 trang 39 Toán lớp 10 Tập 1: Một công ty cần mua các tủ đựng hồ sơ. Có hai loại tủ : Tủ loại A chiếm 3 m² sàn, loại này có sức chứa 12 m³ và có giá 7,5 triệu đồng ; tủ loại B chiếm 6 m² sàn, loại này có sức chứa 18 m³ và có giá 5 triệu. Cho biết công ty chỉ thu xếp được nhiều nhất là 60 m² mặt bằng cho chỗ đựng hồ sơ và ngân sách mua tủ không quá 60 triệu đồng. Hãy lập kế hoạch mua sắm để công ty có thể được thể tích đựng hồ sơ lớn nhất.

Lời giải:

Gọi x và y lần lượt là kích thước của tủ hồ sơ loại A và loại B (x ≥ 0, y ≥ 0)

Theo đề ta có:

+ Công ty chỉ thu xếp được nhiều nhất là 60 m² mặt bằng cho chỗ đựng hồ sơ nên

3x + 6y ≤ 60 hay x + 2y ≤ 20.

+ Ngân sách được sử dụng để mua tủ không quá 60 triệu đồng nên 7,5x + 5y ≤ 60.

Suy ra hệ bất phương trình mô tả các điều kiện ràng buộc là: $\left\{\begin{array}{l}x+2y\le 20\\ 7,5x+5y\le 60\\ x\ge 0\\ y\ge 0\end{array}\right.$

Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy:

+ Xác định miền nghiệm của bất phương trình : x + 2y ≤ 20

Vẽ đường thẳng x + 2y - 20 = 0 đi qua hai điểm (20; 0) và (0; 10).

Xét gốc toạ độ O(0; 0) ta thấy: O không thuộc đường thẳng x + 2y – 20 = 0 và 0 + 2.0 – 20 = - 20  < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Xác định miền nghiệm của bất phương trình : 7,5x + 5y ≤ 60

Vẽ đường thẳng 7,5x + 5y – 60 = 0 đi qua hai điểm (8; 0) và (0; 12).

Xét gốc toạ độ O(0; 0) ta thấy: O không thuộc đường thẳng 7,5x + 5y – 60 = 0 và 7,5.0 + 5.0 – 60 = -60 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng phía trên trục hoành

+ Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng phía bên phải trục tung

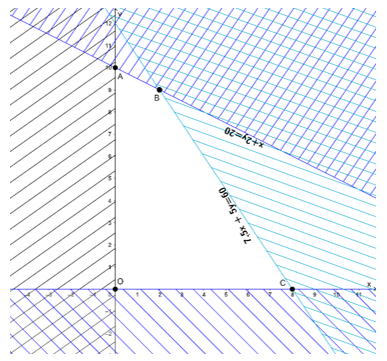
Miền nghiệm là tứ giác OABC với các đỉnh O(0; 0); A(0; 10); B(2; 9) ;C(8; 0).

Gọi F là thể tích để đựng hồ sơ (đơn vị: m³), ta được: F = 12x + 18y.   

Giá trị của F tại các đỉnh của tứ giác:

Tại O(0; 0) ta có: F = 12.0 + 18.0 = 0;

Tại A(0; 10) ta có: F = 12.0 + 18.10 = 180;

Tại B(2; 9) ta có: F = 12.2 + 18.9 = 186;

Tại C(8; 0) ta có: F = 12.8 + 18.0 = 96;

F đạt giá trị lớn nhất bằng 186 tại B(2; 9).

Vậy công ty cần phải mua 2 tủ loại A và 9 tủ loại B để có thể tích đựng hồ sơ lớn nhất.