Cho tam giác ABC vuông tại A có góc B = 60 °. Trên cạnh BC lấy điểm M sao cho góc CAM = 30 °

Lời giải Bài 4.39 trang 87 Toán 7 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7 Tập 1.

243
« Trang trước
Chia sẻ
Trang sau »

Giải Toán 7 Bài tập cuối chương 4 trang 87 

Bài 4.39 trang 87 Toán 7 Tập 1: Cho tam giác ABC vuông tại A có B^=60°. Trên cạnh BC lấy điểm M sao cho CAM^=30°. Chứng minh rằng:

a) Tam giác CAM cân tại M;

b) Tam giác BAM là tam giác đều;

c) M là trung điểm của đoạn thẳng BC.

Lời giải: 

GT

ΔABC vuông tại A, B^=60°;

M∈BC, CAM^=30°.

KL

a) Tam giác CAM cân tại M;

b) Tam giác BAM là tam giác đều;

c) M là trung điểm của đoạn thẳng BC.

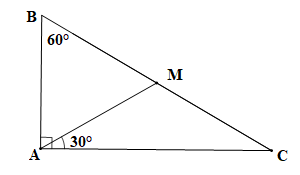
Tài liệu VietJack

a) Tam giác ABC vuông tại A (theo giả thiết) nên hai góc nhọn phụ nhau, do đó

B^+C^=90°.

Suy ra C^=90°−B^

Mà  B^=60° nên C^=90°−60°=30°

Xét tam giác CAM có CAM^=C^=30° nên tam giác CAM là tam giác cân tại M.

b) Ta có CAM^<CAB^ (do 30° < 90°) nên tia AM nằm giữa hai tia AB và AC.

Khi đó CAB^=CAM^+MAB^.

Suy ra MAB^=CAB^−CAM^=90°−30°=60°.

Áp dụng định lí tổng ba góc trong tam giác cho tam giác BAM có: MAB^+B^+AMB^=180°.

Suy ra AMB^=180°−B^−MAB^.

AMB^=180°−60°−60°=60°.

Khi đó AMB^=B^=MAB^=60°.

Suy ra tam giác BAM là tam giác đều.

c) Tam giác AMC cân tại M (chứng minh câu a) nên MA = MC (định nghĩa tam giác cân).

Tam giác BAM là tam giác đều (chứng minh câu b) nên MA = MB (định nghĩa tam giác đều).

Suy ra MB = MC (= MA).

Mà M nằm trên cạnh BC (theo giả thiết)

Do đó M là trung điểm của BC. 

 

Xem thêm lời giải bài tập Toán 7 Tập 1 Kết nối tri thức hay, chi tiết khác:

Bài 4.33 trang 87 Toán 7 Tập 1: Tính các số đo x, y trong các tam giác dưới đây (H.4.75)

Bài 4.34 trang 87 Toán 7 Tập 1: Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng góc MAN = góc MBN

Bài 4.35 trang 87 Toán 7 Tập 1: Trong Hình 4.77, có AO = BO, góc OAM = góc OBN. Chứng minh rằng AM = BN

Bài 4.36 trang 87 Toán 7 Tập 1: Trong Hình 4.78, ta có AN = BM, góc BAN = góc ABM. Chứng minh rằng góc BAM = góc ABN

Bài 4.37 trang 87 Toán 7 Tập 1: Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Chứng minh rằng MB = NB và góc AMB bằng góc ANB

Bài 4.38 trang 87 Toán 7 Tập 1: Cho tam giác ABC cân tại A có góc A = 120 °. Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC

Bài 4.39 trang 87 Toán 7 Tập 1: Cho tam giác ABC vuông tại A có góc B = 60 °. Trên cạnh BC lấy điểm M sao cho góc CAM = 30 °

Bài viết liên quan

243
« Trang trước
Chia sẻ
Trang sau »

Nội dung bài viết

    Xem thêm

    Có thể bạn quan tâm

    Bài viết có lượt xem cao