Cho tam giác ABC cân tại A có góc A = 120 °. Trên cạnh BC lấy hai điểm M, N sao cho MA

Lời giải Bài 4.38 trang 87 Toán 7 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7 Tập 1.

367
« Trang trước
Chia sẻ
Trang sau »

Giải Toán 7 Bài tập cuối chương 4 trang 87 

Bài 4.38 trang 87 Toán 7 Tập 1: Cho tam giác ABC cân tại A có A^=120°. Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:

a) ΔBAM=ΔCAN;

b) Các tam giác ANB, AMC lần lượt cân tại N, M.

Lời giải: 

GT

ΔABC cân tại A, A^=120°;

M,N∈BC;MA⊥AB,NA⊥AC. 

KL

a) ΔBAM=ΔCAN;

b) Tam giác ANB cân tại N, tam giác AMC cân tại M.

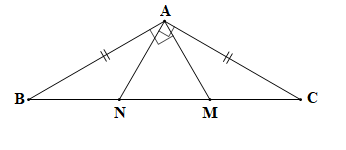
Tài liệu VietJack

a) Tam giác ABC cân tại A (theo giả thiết) nên AB = AC và B^=C^.

MA⊥AB tại A (theo giả thiết) nên BAM^=90°; NA⊥AC tại A (theo giả thiết) nên

NAC^=90°;

Xét tam giác BAM (vuông tại A) và tam giác CAN (vuông tại A) có:

AB = AC (chứng minh trên);

B^=C^ (chứng minh trên).

Vậy ΔBAM=ΔCAN (cạnh góc vuông – góc nhọn kề).

b) Trong tam giác ABC có A^+B^+C^=180° (định lí tổng ba góc trong một tam giác).

Suy ra B^+C^=180°−A^.

Mà A^=120° (theo giả thiết) và B^=C^ (chứng minh trên).

Do đó B^+B^=180°−120°

2B^=60°

B^=30°

Khi đó B^=C^=30°.        (1)

Ta có: BAM^<BAC^ (do 90° < 120°) nên tia AM nằm giữa hai tia AB và AC.

Do đó BAC^=BAM^+MAC^.

Suy ra MAC^=BAC^−BAM^=120°−90°=30°.   

Vậy MAC^=30°.            (2)

Tương tự ta cũng có BAC^=BAN^+NAC^.

Suy ra BAN^=BAC^−NAC^=120°−90°=30°.

Vậy BAN^=30°.            (3)

Từ (1), (2) và (3) ta có:

B^=C^=MAC^=BAN^=30°.

Do đó tam giác ABN cân tại N (do B^=BAN^);

Và tam giác ACM cân tại M (do C^=MAC^). 

 

Xem thêm lời giải bài tập Toán 7 Tập 1 Kết nối tri thức hay, chi tiết khác:

Bài 4.33 trang 87 Toán 7 Tập 1: Tính các số đo x, y trong các tam giác dưới đây (H.4.75)

Bài 4.34 trang 87 Toán 7 Tập 1: Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng góc MAN = góc MBN

Bài 4.35 trang 87 Toán 7 Tập 1: Trong Hình 4.77, có AO = BO, góc OAM = góc OBN. Chứng minh rằng AM = BN

Bài 4.36 trang 87 Toán 7 Tập 1: Trong Hình 4.78, ta có AN = BM, góc BAN = góc ABM. Chứng minh rằng góc BAM = góc ABN

Bài 4.37 trang 87 Toán 7 Tập 1: Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Chứng minh rằng MB = NB và góc AMB bằng góc ANB

Bài 4.38 trang 87 Toán 7 Tập 1: Cho tam giác ABC cân tại A có góc A = 120 °. Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC

Bài 4.39 trang 87 Toán 7 Tập 1: Cho tam giác ABC vuông tại A có góc B = 60 °. Trên cạnh BC lấy điểm M sao cho góc CAM = 30 °

Bài viết liên quan

367
« Trang trước
Chia sẻ
Trang sau »

Nội dung bài viết

    Xem thêm

    Có thể bạn quan tâm

    Bài viết có lượt xem cao