Một vận động viên chạy xe đạp trong 1 giờ 30 phút đầu với vận tốc trung bình là 42km/h
Lời giải Bài 4 trang 59 Toán 10 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.
Giải Toán lớp 10 Bài tập cuối chương 3
Bài 4 trang 59 Toán lớp 10 Tập 1: Một vận động viên chạy xe đạp trong 1 giờ 30 phút đầu với vận tốc trung bình là 42km/h. Sau đó người này nghỉ tại chỗ 15 phút và tiếp tục đạp xe 2 giờ liền với vận tốc 30km/h.
a) Hãy biểu thị quãng đường s (tính bằng ki lô mét) mà người này đi được sau t phút bằng một hàm số.
b) Vẽ đồ thị biểu diễn hàm số s theo t.
Lời giải:
Đổi: 42 km/h = 0,7 km/phút, 30 km/h = 0,5 km/phút
a) Trong 1 giờ 30 phút = 90 phút đầu với vận tốc trung bình là 42 km/h nên ta có:
Với 0 ≤ t ≤ 90 thì s = f(t) = 0,7t
Sau đó, người này nghỉ tại chỗ 15 phút nên ta có:
Với 90 < t ≤ 105 thì s = f(t) = 0,7 . 90 = 63
Người đó tiếp tục đạp xe 2 giờ = 120 phút liền với vận tốc 30 km/h nên ta có:
Với 105 < t ≤ 225 thì s = f(t) = 63 + 0,5 . (t – 105) = 63 + 0,5t – 52,5 = 10,5 + 0,5t.
Vậy ta có hàm số như sau: .
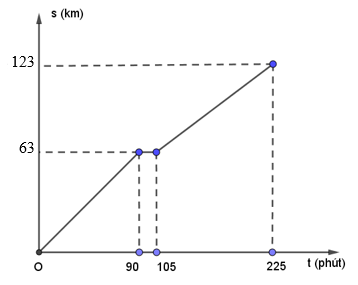
b) Trong đoạn [0; 90], đồ thị hàm số là đường thẳng đi qua điểm (0; 0) và (90; 63).
Trong khoảng (90; 105], đồ thị hàm số là đường thẳng s = 63, song song với trục Ot.
Trong khoảng (105; 120], đồ thị hàm số là đường thẳng đi qua điểm (225; 123).
Ta có đồ thị như hình vẽ: