Cho tam giác ABC có BC = a, AC = b, AB = c và (I; r) là đường tròn nội tiếp tam giác
Lời giải Khám phá 4 trang 70 Toán 10 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.
Giải Toán lớp 10 Bài 2: Định lí côsin và định lí sin
Khám phá 4 trang 70 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = a, AC = b, AB = c và (I; r) là đường tròn nội tiếp tam giác (Hình 11).
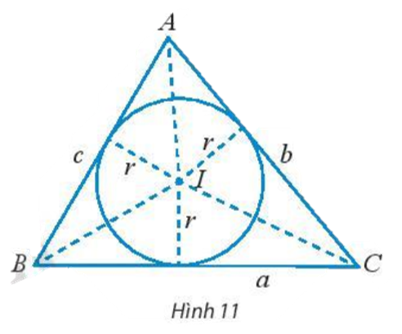
a) Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.
b) Dùng công thức trên để chứng minh công thức tính diện tích tam giác ABC:
Lời giải:
a)
Tương tự ta có:
b) (đpcm)
Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 3 trang 71 Toán lớp 10 Tập 1: Tính diện tích một cánh buồm hình tam giác. Biết cánh buồm đó có chiều dài một cạnh là 3,2 m
Vận dụng 3 trang 72 Toán lớp 10 Tập 1: Tính độ dài cạnh x trong các tam giác sau
Bài 1 trang 72 Toán lớp 10 Tập 1: Tính độ dài cạnh c trong tam giác ABC ở Hình 14
Bài 2 trang 72 Toán lớp 10 Tập 1: Cho tam giác ABC, biết cạnh a = 152, góc B = 79o, góc C = 61o. Tính các góc, các cạnh còn lại
Bài 3 trang 72 Toán lớp 10 Tập 1: Một công viên có dạng hình tam giác với các kích thước như Hình 15


