Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K
Lời giải Bài 7 trang 93 Toán 10 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.
Bài 7 trang 93 Toán lớp 10 Tập 1: Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn: ; . Tính độ dài các vectơ .
Lời giải:
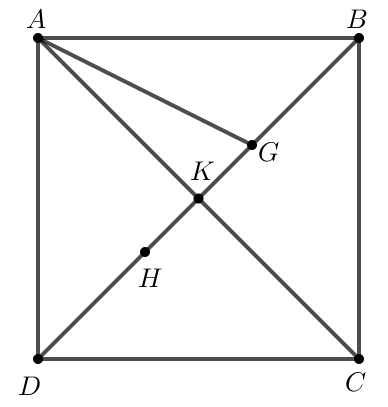
Do nên K là trung điểm của AC.
Do đó K là giao điểm hai đường chéo của hình vuông ABCD.
Do nên G là trọng tâm của tam giác ABC.
Khi đó trên đoạn BK chọn điểm G sao cho .
Do nên H là trọng tâm của tam giác ADC.
Khi đó trên đoạn DK chọn điểm H sao cho .
Áp dụng định lí Pythagore vào tam giác ADC vuông tại D có:
AC2 = AD2 + DC2
AC2 = a2 + a2
AC2 = 2a2
AC = a (do AC là độ dài đoạn thẳng nên AC > 0)
Do K là trung điểm của AC nên AK = AC = .
Do đó .
Do ABCD là hình vuông nên AC = BD.
Do đó BD = a.
Do H là trọng tâm của tam giác ADC nên HK = DK = BD = BD = .
Do G là trọng tâm của tam giác ABC nên KG = BK = BD = BD = .
Do đó HK + KG = + hay HG = .
Do đó .
Do ABCD là hình vuông là K là giao điểm hai đường chéo nên AC BD tại K.
Áp dụng định lí Pythagore vào tam giác AKG vuông tại K có:
AG2 = AK2 + KG2
AG2 =
AG2 =
AG = (do AG là độ dài đoạn thẳng nên AG > 0)
Do đó .
Vậy ; ; .


