Chứng minh rằng với mọi góc Alpha (0 độ nhỏ hơn bằng Alpha nhỏ hơn bằng 180 độ), ta đều có

Lời giải Bài 5 trang 65 Toán 10 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.

375
« Trang trước
Chia sẻ
Trang sau »

Giải Toán lớp 10 Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°

Bài 5 trang 65 Toán lớp 10 Tập 1: Chứng minh rằng với mọi góc α (0° ≤ α  ≤ 180°), ta đều có:

a) cos2α  + sin2α  = 1;

b) tanα  . cotα  = 1 (0° < α  < 180°, α  ≠ 90°).

c) 1 + tan2α  = 1cos2α (α  ≠ 90°);

d) 1 + cot2 α  = 1sin2α (0° < α  < 180°).

Lời giải:

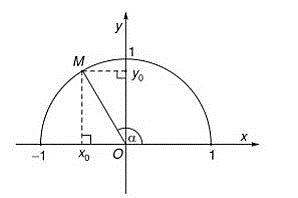
Giải Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ - Chân trời sáng tạo (ảnh 1)

Gọi M là điểm thuộc nửa đường tròn đơn vị sao cho xOM^=α(00≤α≤1800). Khi đó, ta có:

sinα=y0;cosα=x0,tanα=y0x0;cotα=x0y0

a)cos2α+sin2α=x02+y02=OM2=1. Vậy cos2α+sin2α=1.

b) Với 00<α<1800; α ≠ 900: 

tanα. cotα = y0x0.x0y0=1y0x0.x0y0=1

Vậy tanα. cotα =1 (00<α<1800; α ≠ 900).

c) 1+tan2α=1+sin2αcos2α=cos2α+sin2αcos2α=1cos2α(α≠900).

Vậy 1+tan2α=1cos2α(α≠900).       

d) 1+cot2α=1+cos2αsin2α=sin2α+cos2αsin2α=1sin2α(00<α<1800).

Vậy 1+cot2α=1sin2α(00<α<1800).

Bài viết liên quan

375
« Trang trước
Chia sẻ
Trang sau »

Nội dung bài viết

    Xem thêm

    Có thể bạn quan tâm

    Bài viết có lượt xem cao