Giải Toán 7 (Kết nối tri thức) Bài 5: Làm quen với số thập phân vô hạn tuần hoàn
Hoidap.vietjack.com trân trọng giới thiệu: lời giải bài tập Toán lớp 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoàn sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 Bài 5. Mời các bạn đón xem:
Giải bài tập Toán 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoàn
Video giải bài tập Toán 7 Bài 5: Làm quen với số thập phân vô hạn tuần hoàn
Mở đầu
Hình tròn: Mình cũng đặt tính chia mà sao mãi không ra kết quả nhỉ?

Lời giải:
Bạn Hình vuông đã thực hiện đặt phép chia như sau:
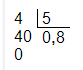
Suy ra
Bạn Hình tròn đã thực hiện đặt phép chia như sau
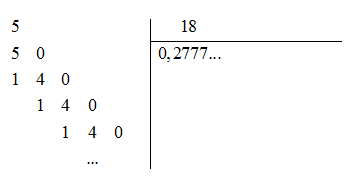
Suy ra
Nhận xét:
Phép chia 4 cho 5 sau khi đặt phép chia ta thấy đây là phép chia hết được thương 0,8 là số thập phân hữu hạn.
Khi thực hiện đặt phép tính chia 5 cho 18 ta thấy phép chia này là một phép chia không bao giờ chấm dứt và nếu cứ tiếp tục thực hiện chia thì trong thương nhận được quan sát thấy chữ số 7 được lặp lại mãi. Ta nói phân số viết được dưới dạng số thập phân 0,2777… và đây là số thập phân vô hạn tuần hoàn.
Số thập phân vô hạn tuần hoàn
Lời giải:
Ta thực hiện đặt phép tính chia như sau:
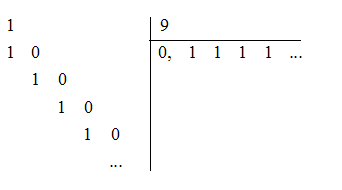
Suy ra
Nhận xét: Khi thực hiện phép tính chia 1 cho 9, ta thấy phép chia này là phép chia không bao giờ chấm dứt và nếu cứ tiếp tục thực hiện chia thì thương nhận được là 0,1111… với chữ số 1 được lặp lại mãi mãi. Vậy kết quả của phép chia 1 cho 9 được viết dưới dạng số thập phân là 0,1111… Đây là số thập phân vô hạn tuần hoàn.
Chỉ ra chu kì rồi viết gọn nếu đó là số thập phân vô hạn tuần hoàn.
Lời giải:
+) Sau khi thực hiện đặt phép tính chia ta có:
+) Sau khi thực hiện đặt phép tính chia ta có:
Vậy phân số viết dưới dạng số thập phân là 0,1818181818…
Nhận thấy đây là số thập phân vô hạn tuần hoàn với chu kì là 18.
Do đó ta có thể viết rút gọn như sau: = -0,(18)
Làm tròn số thập phân căn cứ vào độ chính xác cho trước
Luyện tập 2 trang 28 Toán 7 Tập 1: Làm tròn số 3,14159 với độ chính xác 0,005.
Lời giải:
Để kết quả làm tròn có độ chính xác 0,005 thì hàng làm tròn ta cần thực hiện làm tròn là hàng phần trăm.
Áp dụng quy tắc làm tròn ta được kết quả là: 3,14159 ≈ 3,14.
Lời giải:
+) Làm tròn hai thừa số đến hàng đơn vị:
Số 31,(81) là số thập phân vô hạn tuần hoàn có chu kì là 81 nên 31,(81) = 31,818181… Do đó khi làm tròn đến hàng đơn vị ta được kết quả là: 32
Số 4,9 khi làm tròn đến hàng đơn vị ta được kết quả là 5.
+) Ước lượng kết quả phép tính 31,(81).4,9
Sau khi làm tròn ta được phép tính mới là: 32.5.
Khi đó ước lượng kết quả phép tính là: 31,(81) . 4,9 ≈ 32.5 = 160.
Vậy kết quả của phép tính 31,(81).4,9 xấp xỉ 160.
Bài tập
0,1; –1,(23); 11,2(3); –6,725.
Lời giải:
Ta thấy:
+) Số –1,(23) được viết dưới dạng rút gọn có chu kì là 23 nên là số thập phân vô hạn tuần hoàn.
+) Số 11,2(3) được viết dưới dạng rút gọn có chu kì là 3 nên là số thập phân vô hạn tuần hoàn.
Vậy trong các số thập phân trên thì:
- Các số thập phân hữu hạn là: 0,1; –6,725.
- Các số thập phân vô hạn tuần hoàn là: –1,(23); 11,2(3).
Bài 2.2 trang 28 Toán 7 Tập 1: Sử dụng chu kì, hãy viết gọn số thập phân vô hạn tuần hoàn 0,010101…
Lời giải:
Ta nhìn số 0,010101… thì số 01 được lặp lại mãi nên chu kì của số thập phân vô hạn tuần hoàn này là 01.
Viết gọn số thập phân vô hạn tuần hoàn ta được: 0,010101… = 0,(01).
Lời giải:
Ta thấy số 3,2(31) là số thập phân vô hạn tuần hoàn có chu kì là 31 nên ta có:
3,2(31) = 3,2313131…
Do đó chữ số thập phân thứ năm của số 3,2(31) là 1.
Áp dụng quy tắc làm tròn để làm tròn số 3,2(31) đến chữ số thập phân thứ năm ta được kết quả là: 3,23131.
Lời giải:
Quan sát số 0,1010010001000010… (viết liên tiếp các số 10, 100, 1 000, 10 000, … sau dấu phẩy) ta không tìm được chu kì của số này.
Do đó số 0,1010010001000010… không phải là số thập phân vô hạn tuần hoàn.
Bài 2.5 trang 28 Toán 7 Tập 1: Làm tròn số 3,14159…
a) đến chữ số thập phân thứ ba;
Lời giải:
a) Áp dụng quy tắc làm tròn để làm tròn số 3,14159… đến chữ số thập phân thứ ba ta được kết quả là 3,142.
b) Làm tròn số 3,14159… với độ chính xác 0,005 tức là làm tròn số tới hàng phần trăm.
Áp dụng quy tắc làm tròn ta được kết quả là 3,14.


