Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao

Lời giải Bài 9 trang 73 Toán 10 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.

231

« Trang trước

Trang sau »

Giải Toán lớp 10 Bài 2: Định lí côsin và định lí sin

Bài 9 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.

a) Chứng minh $\frac{S_{B D E}}{S_{B A C}} = \frac{B D . B E}{B A . B C}$

b) Biết rằng S_ABC = 9S_BDE và DE = $2 \sqrt{2}$ . Tính cosB và bán kính đường tròn ngoại tiếp tam giác ABC.

Lời giải:

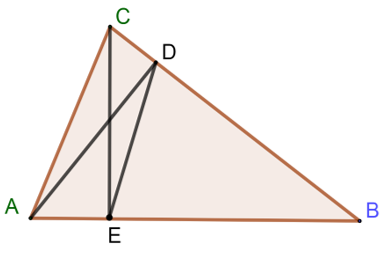
Giải Toán 10 Bài 2: Định lí côsin và định lí sin - Chân trời sáng tạo (ảnh 1)

a) Ta có: $\frac{S_{B D E}}{S_{B A C}} = \frac{\frac{1}{2} . B E . B D . \sin B}{\frac{1}{2} . B A . B C . \sin B} = \frac{B E . B D}{B A . B C}$

b) Theo đề ta có: $\frac{S_{B D E}}{S_{A B C}} = \frac{B D . B E}{B A . B C} = \frac{B D}{B A} . \frac{B E}{B C} = \frac{1}{9}$ (1)

Xét tam giác BCE vuông tại E ta có: $\cos B = \frac{B E}{B C}$ (2)

Xét tam giác BDA vuông tại D ta có: $\cos B = \frac{B D}{B A}$ (3)

Thay (2) và (3) vào (1) ta được : $\cos^{2} B = \frac{1}{9} \Rightarrow \cos B = \frac{1}{3}$ ( Vì góc B nhọn)

Mặt khác, $\sin^{2} B + \cos^{2} B = 1 \Rightarrow \sin^{2} B = 1 - \frac{1}{9} = \frac{8}{9} \Rightarrow \sin B = \frac{2 \sqrt{2}}{3}$

Áp dụng định lí sin cho tam giác BED ta có: $R^{'} = \frac{E D}{2 \sin B} = \frac{3}{2}$

Xét tam giác BED và BCA ta có:

Góc B chung

$\frac{B E}{B C} = \frac{1}{3}$ và $\frac{B D}{B A} = \frac{1}{3}$

Vậy tam giác AED đồng dạng với tam giác BCA nên $\frac{E D}{C A} = \frac{1}{3}$

Theo đề ta có:

$\frac{S_{B D E}}{S_{A B C}} = \frac{\frac{B D . B E . D E}{4 R'}}{\frac{B A . B C . A C}{4 R}} = \frac{B D}{B A} . \frac{B E}{B C} . \frac{D E}{A C} . \frac{R}{R^{'}} = \frac{1}{27} . \frac{R}{R^{'}} = \frac{1}{9}$ $\Rightarrow R = 3 R^{'} = 3. \frac{3}{2} = \frac{9}{2}$