Cho tam giác ABC không phải là tam giác vuông với góc A nhọn

Lời giải Khám phá 1 trang 66 Toán 10 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.

193
« Trang trước
Chia sẻ
Trang sau »

Giải Toán lớp 10 Bài 2: Định lí côsin và định lí sin

Khám phá 1 trang 66 Toán lớp 10 tập 1:

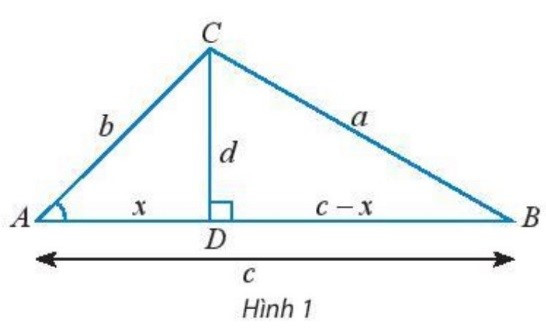
Cho tam giác ABC không phải là tam giác vuông với góc A nhọn (ảnh 1)

a) Cho tam giác ABC không phải là tam giác vuông với góc A nhọn và C^≥B^.Vẽ đường cao CD và đặt tên các độ dài như trong hình 1. Hãy thay dấu ? bằng chữ cái thích hợp để chứng minh công thức a2=b2+c2−2bccosA theo gợi ý sau:

Xét tam giác vuông BCD , ta có: a2=d2+(c−x)2=d2+c2+x2−2cx (1)

Xét tam giác vuông ACD, ta có:   b2=d2+x2⇒d2=b2−x2                (2)

                                                     cosA=?b⇒?=bcosA                  (3)          

Thay (2) và (3) vào (1), ta có : a2=b2+c2−2bccosA

b) Cho tam giác ABC với góc A tù. Làm tương tự như trên chứng minh rằng ta cũng có:

c) Cho tam giác ABC vuông tại A.Hãy chứng tỏ công thức a2=b2+c2−2bccosA có thể viết là a2=b2+c2

Lời giải

a) Xét tam giác vuông BCD , ta có: a2=d2+(c−x)2=d2+c2+x2−2cx (1)

Xét tam giác vuông ACD, ta có:   b2=d2+x2⇒d2=b2−x2                    (2)

                                                     cosA=xb⇒x=bcosA                       (3)          

Thay (2) và (3) vào (1), ta có : a2=b2+c2−2bccosA

b)

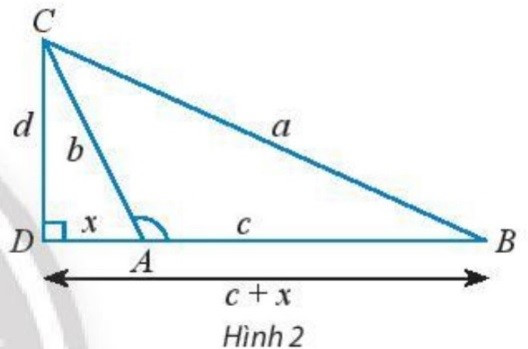
Cho tam giác ABC không phải là tam giác vuông với góc A nhọn (ảnh 1)

Xét tam giác vuông BCD , ta có: a2=d2+(c+x)2=d2+c2+x2+2cx     (1)

Xét tam giác vuông ACD, ta có:   b2=d2+x2⇒d2=b2−x2                    (2)

                      Vì A là góc tù nên  cosA=−xb⇒x=−bcosA                      (3)          

Thay (2) và (3) vào (1), ta có : a2=b2+c2−2bccosA         

c)

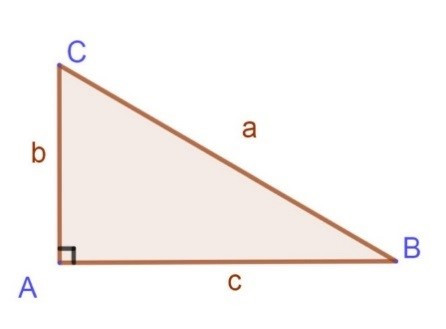
Cho tam giác ABC không phải là tam giác vuông với góc A nhọn (ảnh 1)

Theo đề ta có : a2=b2+c2−2bccosA

Mà cosA=cos900=0

Nên a2=b2+c2−2bc.0=c2+b2a2=b2+c2−2bccosA

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài viết liên quan

193
« Trang trước
Chia sẻ
Trang sau »

Nội dung bài viết

    Xem thêm

    Có thể bạn quan tâm

    Bài viết có lượt xem cao