Vận dụng trang 23 Toán lớp 6 Tập 1:

(1) Tính số hạt thóc có trong ô thứ 7 của bàn cờ nói trong bài toán mở đầu.

(2) Hãy viết mỗi số tự nhiên sau thành tổng giá trị các chữ số của nó bằng cách dùng các lũy thừa của 10 theo mẫu:

4 257 = 4 . 103 + 2. 102 + 5 . 10 + 7.

a) 23 917;

b) 203 184.

Lời giải:

(1) Số hạt thóc có trong ô thứ 7 của bàn cờ nói trong bài toán mở đầu:

                             2 . 2 . 2 . 2 . 2 . 2 = 26 = 64 (hạt thóc)

Vậy trong ô thứ 7 của bàn cờ vua nói trong bài toán mở đầu có 64 hạt thóc.

(2) Theo mẫu đã cho, ta viết được như sau:

a) 23 197 = 2 . 104 + 3 . 103 + 1 . 102 + 9 . 10 + 7.

b) 203 184 = 2 . 105 + 0 . 104 + 3 . 103 + 1 . 102 + 8 . 10 + 4.

Hoạt động 2 trang 23 Toán lớp 6 Tập 1:

a) Viết kết quả phép nhân sau dưới dạng một lũy thừa của 7:

72.73 = (7 . 7) . (7 . 7 . 7) = ?

b) Nêu nhận xét về mối liên hệ giữa các số mũ của 7 trong hai thừa số và trong tích tìm được ở câu a).

Lời giải:

a)72.73 = (7.7).(7.7.7) = 7.7.7.7.7 = 75

b) Ta thấy 2 + 3 = 5 

Nên ta có nhận xét: Tổng số mũ của 7 trong hai thừa số bằng số mũ của tích tìm được.

Luyện tập 2 trang 23 Toán lớp 6 Tập 1: Viết kết quả phép tính dưới dạng một lũy thừa:

a) 53 . 57

b) 24 . 25 . 29

c) 102 . 104 . 106 . 108

Lời giải:

a) 53 . 57 = 53 + 7 = 510

b) 24 . 25 . 29 = 24 + 5 + 9 = 218

c) 102 . 104 . 106 . 108 = 102 + 4 + 6 + 8 = 1020

Hoạt động 3 trang 24 Toán lớp 6 Tập 1:

a) Giải thích vì sao có thể viết 65 = 63 . 62

b) Sử dụng câu a) để suy ra 65 : 63 = 62. Nêu nhận xét về mối liên hệ giữa các số mũ của 6 trong số bị chia, số chia và thương.

c) Viết thương của phép chia 107 : 104 dưới dạng lũy thừa của 10.

Lời giải:

a) Ta có: 63 . 62 = 63 + 2 = 65 nên có thể viết 65 = 63 . 62

b) Ta có 65 = 63 . 62 nên 65 : 63 = 62

Ta thấy 5 - 3 = 2

Nên ta có nhận xét: Hiệu số mũ của 6 trong số bị chia và số chia bằng số mũ của 6 trong thương tìm được.

c) Ta nhận thấy 107 = 104 + 3 = 104 . 103 nên 107 : 104 = 103

Luyện tập 3 trang 24 Toán lớp 6 Tập 1:

Viết kết quả các phép tính dưới dạng một lũy thừa:

a)   76 : 74

b)  1091100 : 1091100 

Lời giải:

a) 76 : 74 = 76-4 = 72 .

b) 1091100 : 1091100 =1091100 - 100 = 10910 = 1 = 11

Bài tập

Bài 1.36 trang 24 Toán lớp 6 Tập 1: Viết các tích sau dưới dạng một lũy thừa:

a) 9 . 9 . 9 . 9 . 9

b) 10 . 10 . 10 . 10

c) 5 . 5 . 5 . 25

d) a . a . a . a . a . a

Lời giải:

a) 9 . 9 . 9 . 9 . 9 = 95

b) 10 . 10 . 10 . 10 = 104

c) 5 . 5 . 5 . 25 = 5 . 5 . 5 . 5 . 5 = 55

d) a . a . a . a . a . a = a6

Bài 1.37 trang 24 Toán lớp 6 Tập 1: Hoàn thành bảng sau vào vở:

Lời giải:

+) Ta có 43 là lũy thừa với cơ số là 4 và số mũ là 3

43 = 4 . 4 .  4 = 16 . 4 = 64

+) Cơ số là 3, số mũ là 5 ta có lũy thừa là 35

35 = 3 . 3 . 3 . 3 . 3 = 9 . 3 . 3 . 3 = 27 . 3 . 3 = 81 . 3 = 243

+) Với cơ số là 2 thì ta phân tích 128 thành tích của các thừa số 2, ta được:

128 = 2 . 2 . 2 . 2 . 2 . 2 . 2 = 27

Vậy ta cần điền các số vào bảng như sau:  

Bài 1.38 trang 24 Toán lớp 6 Tập 1:

Tính: a) 25

b) 33

c) 52

c) 109

Lời giải:

a) 25= 2.2.2.2.2 = 4.2.2.2 = 8.2.2 = 16.2 = 32

b) 33 = 3.3.3 = 9.3 = 27

c) 52 = 5 . 5 = 25.

d) 109 = 10.10.10.10.10.10.10.10.10 = 1 000 000 000.

(Chú ý: Lũy thừa với cơ số là 10 thì số chữ số 0 ở kết quả của lũy thừa chính bằng số mũ).

Bài 1.39 trang 24 Toán lớp 6 Tập 1: Viết các số sau thành tổng giá trị các chữ số của nó bằng cách dùng các lũy thừa của 10: 215; 902; 2 020; 883 001.

Lời giải:

+) 215 = 2. 102 + 1. 101 + 5

+) 902 = 9. 102 + 0. 101 + 2

+) 2 020 = 2. 103 + 0. 102 + 2. 101 + 0

+) 883 001 = 8. 105 + 8. 104 + 3. 103 + 0. 102 + 0. 101 + 1

Bài 1.40 trang 24 Toán lớp 6 Tập 1:

Tính 112, 1112 . Từ đó hãy dự đoán kết quả của 11112.

Lời giải:

+) 112 = 11.11 = 121

+) 1112 = 111.111 = 12321

Dự đoán. 11112 = 1 234 321

Bài 1.41 trang 24 Toán lớp 6 Tập 1:

Biết 210 = 1024. Tính 29 và 211.

Lời giải:

Biết 210 = 1024

Ta có:  29 = 210 – 1 = 210 : 2 = 1024 : 2 = 512.

            211 = 210 + 1 = 210 . 2 = 1024.2 = 2048

Bài 1.42 trang 24 Toán lớp 6 Tập 1:

Tính: a) 57.53                      b) 58 : 54

Lời giải:

a) 57.53 = 57+3 = 510

b) 58 : 54 = 58-4 = 54

Bài 1.43 trang 24 Toán lớp 6 Tập 1:

Ta có: 1 + 3 + 5 = 9 = 32.

Viết các tổng sau dưới dạng bình phương của một số tự nhiên:

a) 1 + 3 + 5 + 7

b) 1 + 3 + 5 + 7 + 9.

Lời giải:

a) Ta có: 1 + 3 + 5 + 7 = 16 = 4.4 = 42

b) Ta có: 1 + 3 + 5 + 7 + 9 = 25 = 5.5 = 52

Bài 1.44 trang 24 Toán lớp 6 Tập 1:

Trái Đất có khối lượng khoảng 60.1020 tấn. Mỗi giây Mặt Trời tiêu thụ 6.106 tấn khí hydrogen (theo vnexpress.net). Hỏi Mặt Trời cần bao nhiêu giây để tiêu thụ một lượng khí hydrogen có khối lượng bằng khối lượng Trái Đất?

Lời giải:

Thời gian để Mặt Trời tiêu thụ một lượng khí hdrogen có khối lượng bằng khối lượng Trái Đất là:

(60. 1020) : ( 6. 106)

= (6.10.1020):(6.106) = 6.1021 : 6 : 106 = (6:6).(1021:106) = 1021-6 = 1015 (giây)

Vậy Mặt Trời cần 1015 giây để tiêu thụ một lượng khí hydrogen.

Bài 1.45 trang 24 Toán lớp 6 Tập 1:

Theo các nhà khoa học, mỗi giây cơ thể con người trung bình tạo ra khoảng 25.105 tế bào hồng cầu (theowww.healthline.com). Hãy tính xem mỗi giờ, bao nhiêu tế bào hồng cầu được tạo ra?

Lời giải:

Đổi 1 giờ = 3 600 giây

Vậy mỗi giờ số tế bào hồng cầu được tạo ra là:

25.105. 3 600 = 3 600. 25. 105 = 36.10.10.25.105 = (36.25).107 = 900.107 = 9.102.107 = 9.109 (tế bào) 

Vậy mỗi giờ có 9.109 tế bào hồng cầu được tạo ra.

Phần 2: Lý thuyết bài học 

Với tóm tắt lý thuyết Toán lớp 6 Bài 6: Lũy thừa với số mũ tự nhiên hay nhất, chi tiết sách Kết nối tri thức với cuộc sống sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 6.

A. Lý thuyết

+ Lũy thừa bậc n của số tự nhiên a là tích của n thừa số bằng nhau, mỗi thừa số bằng a: 

an = 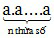(n ∈ N*)

an đọc là “a mũ n” hoặc “ a lũy thừa n”, a là cơ số, n là số mũ.

Chú ý: Ta có a1 = a.

a2 cũng được gọi là a bình phương (hay bình phương của a);

a3 cũng được gọi là a lập phương (hay lập phương của a).

Ví dụ 1. Viết các biểu thức sau dưới dạng lũy thừa:

a) 4.4.4.4.4.4.4;

b) 11.11.11;

c) 8.8.8.8.8.

Lời giải

a) 4.4.4.4.4.4.4 = 47;

b) 11.11.11 = 113;

c) 8.8.8.8.8 = 85.

+ Nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và công các số mũ:

am.an = am+n.

Ví dụ 2. Viết kết quả của các phép tính sau dưới dạng một lũy thừa:

a) a2.a3.a5;

b) 23.28.27;

c) 7.72.723.

Lời giải

a) a2.a3.a5 = a2 + 3 + 5 = a10;

b) 23.28.27 = 23 + 8 + 7 = 218;

c) 7.72.723 = 71 + 2 + 23 = 726.

Chia hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và trừ các số mũ:

am:an = am-n.

Ví dụ 3. Viết kết quả của phép tính dưới dạng một lũy thừa:

a) 1212:12;

b) 108:105:103.

Lời giải

a) 1212:12 = 1212 – 1 = 1211;

b) 108:105:103 = 108 – 5 : 103 = 103 : 103 = 103 – 3 = 100 = 1.

B. Bài tập

Bài 1. Hoàn thành bảng sau: 

Lời giải

Bài 2. Khối lượng của trái đất khoảng 6.1021 tấn. Khối lượng mặt trăng khoảng 7,4.1019 tấn. Hỏi khối lượng trái đất gấp bao nhiêu lần khối lượng mặt trăng.

Lời giải

Khối lượng trái đất gấp số lần khối lượng mặt trăng là: 

6.1021 : (7,4.1019) = 600.1019:(7,4.1019) = (600:7,4) ≈ 81 (lần).

Khối lượng trái đất gấp 81 lần khối lượng mặt trăng.

Phần 3: Bài tập trắc nghiệm

Với 23 bài tập trắc nghiệm Toán lớp 6 Bài 6: Lũy thừa với số mũ tự nhiên có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức với cuộc sống sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 6.

I. Nhận biết

Câu 1. Lũy thừa bậc n của số tự nhiên a được viết là:

A. an;

B. a.n;

C. a + n;

D. a – n.

Câu 2. Cách đọc 22  nào là sai?

A. hai mũ hai;

B. hai lũy thừa hai;

C. hai bình phương;

D. hai nhân hai.

Câu 3. Hãy chỉ ra cơ số của lũy thừa 312

A. Cơ số là 3.

B. Cơ số là 12.

C. Cơ số là 312.

D. Cơ số là 123.

Câu 4. Khi nhân hai lũy thừa cùng cơ số: am.an. Kết quả là:

A. am.n;

B. am+n;

C. am-n;

D. am:n.

Câu 5. Khi chia hai lũy thừa cùng cơ số (khác 0) thì:

A. Ta giữ nguyên cơ số và cộng hai số mũ lại.

B. Ta giữ nguyên cơ số và nhân hai cơ số lại.

C. Ta giữ nguyên cơ số và chia số mũ của số bị chia cho số mũ của số chia.

D. Ta giữ nguyên cơ số và trừ số mũ của số bị chia cho số mũ của số chia.

Câu 6. Chọn phát biểu đúng.

A. a3 còn được gọi là a lập phương.

B. a3 = a + a + a.

C. a3 = a.3.

D. Số mũ của a3 là a.

Câu 7. Viết kết quả của phép tính sau dưới dạng một lũy thừa: 5.5.5.5?

A. 5.4.

B. 54.

C. 55.

D. 53.

Câu 8. Ta có am:an = am – n với điều kiện là gì?

A. a ≠ 0;

B. a ≠ 0 và m < n.

C. a ≠ 0 và m > n.

D. a ≠ 0 và m ≥ n.

Câu 9. Lập phương của 7 được viết như thế nào?

A. 72;                    B. 73;                    C. 7.3;                  D. 7.2.

Câu 10. 16 là lũy thừa của số tự nhiên nào, và có số mũ bằng bao nhiêu?

A. Lũy thừa của 2, số mũ bằng 4

B. Lũy thừa của 4, số mũ bằng 3

C. Lũy thừa của 2, số mũ bằng 3

D. Lũy thừa của 2, số mũ bằng 3

II. Thông hiểu

Câu 1. Tính 23?

A. 6.

B. 8.

C. 12.

D. 16.

Câu 2. Viết tích sau dưới dạng một lũy thừa: 5.5.5.25

A. 53.25;

B. 54;

C. 55;

D.5.252.

Câu 3. Tính 34.53.

A. 157;

B. 151;

C. 10 125;

D. 180.

Câu 4. Viết tổng sau dưới dạng bình phương của một số tự nhiên: 1 + 3 + 5 +7.

A. 42.

B. 162.

C. 22.

D. 82.

Câu 5. Kết quả của phép tính: 719.72:721

A. 7;

B. 1;

C. 72;

D. 73.

Câu 6. Viết số 902 thành tổng giá trị các chữ số của nó bằng cách dùng các lũy thừa của 10.

A. 902 = 9.100 + 2.10;

B. 902 = 9.103 + 0 + 2;

C. 902 = 9.102 + 2;

D. 902 = 9 + 0 + 2.

Câu 7. Cho 210 = 1 024. Hãy tính 211.

A. 211 = 512.

B. 211 = 2 048.

C. 211 = 1 024.

D. 211 = 2 028.

Câu 8. Ghép kết quả ở cột A với các lũy thừa tương ứng ở cột B.

A. 1 – e; 2 – b; 3 – a; 4 – d; 5 – c.

B. 1 – e; 2 – d; 3 – a; 4 – b; 5 – c.

C. 1 – e; 2 – d; 3 – a; 4 – c; 5 – b.

D. 1 – e; 2 – b; 3 – a; 4 – c; 5 – d.

Câu 9. Tìm số n thỏa mãn 4n = 43.45.

A. n = 15;

B. n = 8;

C. n = 7;

D. n = 2.

Câu 10. Tìm số tự nhiên x, biết: x2 = 16.

A. x = 4;

B. x = 2;

C. x = 8;

D. x = 16.

III. Vận dụng

Câu 1. Trái Đất có khối lượng khoảng 60. tấn. Mỗi giây Mặt Trời tiêu thụ 6. tấn khí hydrogen (theo vnexpress.net). Hỏi Mặt Trời cần bao nhiêu giây để tiêu thụ một lượng khí hydrogen có khối lượng bằng khối lượng Trái Đất?

A. 1012;

B. 103;

C. 104;

D. 105.

Câu 2. Theo các nhà khoa học, mỗi giây cơ thể con người trung bình tạo ra khoảng 25. tế bào hồng cầu (theo www.healthline.com). Hãy tính xem mỗi giờ, bao nhiêu tế bào hồng cầu được tạo ra?

A. 9.109;

B. 9.1010;

C. 9.108;

D. 9.1019.

Câu 3. Truyền thuyết Ấn Độ kể rằng người phát minh ra bàn cờ vua đã chọn phần thưởng là số thóc rải trên 64 ô của bàn cờ vua như sau: ô thứ nhất để 1 hạt thóc, ô thứ hai để 2 hạt thóc, ô thứ ba để 4 hạt thóc, ô thứ tư để 8 hạt thóc,… Cứ như thế số hạt ở ô sau gấp đôi số hạt ở ô trước. Hỏi ô số 34 của bàn cờ có bao nhiêu hạt thóc.

A. 234;

B. 34.2;

C. 342;

D. 233.