Bài 11: Ước chung - Ước chung lớn nhất
Bài 11: Ước chung - Ước chung lớn nhất
Bài 11: Ước chung - Ước chung lớn nhất
Phần 1: Giải Sách Giáo Khoa
Trả lời câu hỏi giữa bài
Hoạt động 1 trang 44 Toán lớp 6 Tập 1: Tìm các tập hợp Ư(24) và Ư(28).
Lời giải:
+) Vì 24 chia hết cho các số: 1; 2; 3; 4; 6; 8; 12; 24
Do đó: Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}.
+) Vì 28 chia hết cho các số: 1; 2; 4; 7; 14; 28
Do đó: Ư(28) = {1; 2; 4; 7; 14; 28}.
Hoạt động 2 trang 44 Toán lớp 6 Tập 1:
Gọi ƯC(24, 28) là tập hợp các số vừa là ước của 24, vừa là ước của 28. Hãy viết tập hợp
ƯC(24, 28).
Lời giải:
Ta có: Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ư(28) = {1; 2; 4; 7; 14; 28}
Các số vừa là ước của 24, vừa là ước của 28 là: 1; 2; 4.
Vậy ƯC(24; 28) = {1; 2; 4}.
Hoạt động 3 trang 44 Toán lớp 6 Tập 1: Tìm số lớn nhất trong tập ƯC(24, 28).
Lời giải:
Ta có: ƯC(24; 28) = {1; 2; 4}
Số lớn nhất trong ƯC(24; 28) là 4.
Câu hỏi 1 trang 45 Toán lớp 6 Tập 1: Tìm ƯCLN(90, 10).
Lời giải:
Vì 90 ⁝ 10 nên ta có ƯCLN(90, 10) = 10.
Luyện tập 1 trang 45 Toán lớp 6 Tập 1: Bố có 12 quả bóng màu xanh và 15 quả bóng màu đỏ. Bố muốn chia số bóng cho ba anh em Việt, Hà và Nam đều như nhau gồm cả bóng màu xanh và bóng màu đỏ. Hỏi bố có thực hiện được điều đó hay không?
Lời giải:
Ta có: 12 ⁝ 3, 15 ⁝ 3 hay 3 ∈ Ư(12); 3 ∈ Ư(15)
Nên 3 ∈ ƯC(12; 15) do đó bố chia được số bóng cho ba anh em Việt, Hà và Nam đều như nhau gồm cả bóng màu xanh và bóng màu đỏ.
Vậy bố có thể thực hiện phép chia này.
Vận dụng 1 trang 45 Toán lớp 6 Tập 1:
Tuần này lớp 6A và 6B gồm 40 học sinh nữ và 36 học sinh nam được phân công đi thu gom rác làm sạch bờ biển ở địa phương. Nếu chia nhóm sao cho số học sinh nam và nữ trong các nhóm bằng nhau thì:
a) Có thể chia được thành bao nhiêu nhóm học sinh?
b) Có thể chia nhiều nhất bao nhiêu nhóm học sinh?
Lời giải:
a) Để số học sinh nam và nữ trong các nhóm đều bằng nhau nên số nhóm chính là ước chung của 36 và 40
Gọi x là số nhóm học sinh chia được (nhóm)
Ư(36) = {1; 2; 3; 4; 6; 9; 12; 18; 36}
Ư(40) = {1; 2; 4; 5; 8; 10; 20; 40}
Do đó ƯC(36; 40) = {1; 2; 4}
Số học sinh nam và nữ trong mỗi nhóm được cho như bảng dưới đây:
|
Số nhóm |
Số nam |
Số nữ |
|
1 |
36 : 1 = 36 |
40 : 1 = 40 |
|
2 |
36 : 2 = 18 |
40 : 2 = 20 |
|
4 |
36 : 4 = 9 |
40 : 4 = 10 |
Vậy có thể chia được 1 nhóm; 2 nhóm hoặc 4 nhóm.
b) Số nhóm chia được nhiều nhất là ƯCLN(36; 40)
Vì ƯC(36; 40) = {1; 2; 4} nên ƯCLN(36; 40) = 4.
Vậy có thể chia nhiều nhất 4 nhóm học sinh.
Câu hỏi 2 trang 46 Toán lớp 6 Tập 1:
Tìm ƯCLN(45, 150) biết 45 = 32.5 và 150 = 2.3.52 .
Lời giải:
+) Phân tích các số 45, 150 ra thừa số nguyên tố:
45 = 32.5
150 = 2.3.52
+) Các thừa số nguyên tố chung là: 3; 5
+) Số mũ nhỏ nhất của 3 là 1 và số mũ nhỏ nhất của 5 là 1 nên
ƯCLN(45, 150) = 3. 5 = 15
Vậy ƯCLN(45, 150) = 3. 5 = 15.
Luyện tập 2 trang 46 Toán lớp 6 Tập 1: Tìm ƯCLN(36, 84).
Lời giải:
Phân tích các số 36 và 84 ra thừa số nguyên tố ta được:
36= 22.32; 84 = 22.3.784;
Ta thấy 2 và 3 là các thừa số nguyên tố chung của 36 và 84. Số mũ nhỏ nhất của 2 là 2, số mũ nhỏ nhất của 3 là 1 nên ƯCLN(36, 84) = 22.3 = 12
Vậy ƯCLN(36, 84) = 12.
Vận dụng 2 trang 46 Toán lớp 6 Tập 1: Một đại hội bộ binh có ba trung đội: trung đội I có 24 chiến sĩ, trung đội II có 28 chiến sĩ, trung đội III có 36 chiến sĩ. Trong cuộc diễu binh, cả ba trung đội phải xếp thành các hàng dọc đều nhau mà không có chiến sĩ nào trong mỗi trung đội bị lẻ hàng. Hỏi có thể xếp được nhiều nhất bao nhiêu hàng dọc?
Lời giải:
Vì trong cuộc diễu binh, cả ba trung đội phải xếp thành các hàng dọc đều nhau mà không có chiến sĩ nào trong mỗi trung đội bị lẻ hàng nên số hàng dọc là ƯC(24; 28; 36).
Mặt khác để xếp được nhiều nhất số hàng dọc thì số hàng dọc là ƯCLN(24; 28; 36)
Ta có:
24 = 23.3
28 = 22.7
36 = 22.32
Ta thấy 2 là thừa số nguyên tố chung của 24; 28 và 36. Số mũ nhỏ nhất của 2 là 2 nên ƯCLN(24; 28; 36) = 22 = 4
Vậy có thể xếp được nhiều nhất 4 hàng dọc.
Câu hỏi 3 trang 46 Toán lớp 6 Tập 1: Biết ƯCLN(75; 105) = 15, hãy tìm ƯC(75, 105).
Lời giải:
Vì ƯCLN(75; 105) = 15 nên ƯC(75, 105) = Ư(15) = {1; 3; 5; 15}
Vậy ƯC(75, 105) = {1; 3; 5; 15}.
Thử thách nhỏ trang 47 Toán lớp 6 Tập 1:
Vào ngày thứ Bảy, cô Lan tổ chức cho học sinh đi tham quan Bảo tàng Dân tộc học. Các học sinh đóng tiền mua vé, mỗi em một vé. Số tiền cô Lan thu được từng ngày được ghi lại ở bảng bên.
a) Hỏi số tiền để mua một vé (giá vé được tính theo đơn vị nghìn đồng) có thể là bao nhiêu, biết giá vé lớn hơn 2000 đồng?
b) Có bao nhiêu học sinh tham gia chuyến đi, biết số học sinh trong lớp khoảng từ 20 đến 40 người.
|
Ngày |
Số tiền đóng (đồng) |
|
Thứ hai |
56 000 |
|
Thứ Ba |
28 000 |
|
Thứ Tư |
42 000 |
|
Thứ Năm |
98 000 |
Lời giải:
a) Vì mỗi em mua một vé nên giá vé tính theo nghìn đồng chính là
ƯC(56 000; 28 000; 42 000; 98 000)
Ta có: 56 000 = 26.53.7
28 000 = 25.53.7
42 000 = 24.3.53.7
98 000 = 24.53.72
Ta thấy 2; 5 và 7 là các thừa số nguyên tố chung của 56 000; 28 000; 42 000; 98 000. Số mũ nhỏ nhất của 2 là 4, số mũ nhỏ nhất của 5 là 3, số mũ nhỏ nhất của 7 là 1 nên
ƯCLN (56 000; 28 000; 42 000; 98 000) = 24.53.7 = 14 000
ƯC(56 000; 28 000; 42 000; 98 000) = Ư(14 000)
Do giá vé tính theo đơn vị nghìn đồng nên giá vé chỉ có thể là: 1 000; 2 000; 7 000 đồng.
Mà giá vé lớn hơn 2000 đồng nên giá vé là 7 000 đồng.
b) Tổng số tiền cô Lan thu được thừ thứ Hai đến thứ Năm là:
56 000 + 28 000 + 42 000 + 98 000 = 224 000 (đồng)
Số học sinh tham gia chuyến đi là:
224 000 : 7 000 = 32 (học sinh)
Vậy giá vé là 7 000 đồng và có 32 học sinh tham gia chuyến đi.
Câu hỏi 4 trang 47 Toán lớp 6 Tập 1:
Phân số 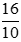 đã là phân số tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản.
đã là phân số tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản.
Lời giải:
Ta có: 16 = 24 ; 10 = 2.5
+) Thừa số nguyên tố chung là: 2 với số mũ nhỏ nhất là 2 nên ƯCLN(16, 10) = 2
Do đó phân số 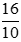 chưa là phân số tối giản nên:
chưa là phân số tối giản nên:
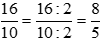 . Ta có
. Ta có 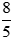 là phân số tối giản vì ƯCLN(8, 5) = 1.
là phân số tối giản vì ƯCLN(8, 5) = 1.
Luyện tập 3 trang 48 Toán lớp 6 Tập 1:
Rút gọn về phân số tối giản: a) 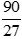 b)
b) 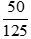
Lời giải:
a) Ta có: 90 = 2.33.5; 27 = 33
+) Thừa số nguyên tố chung là: 3 với số mũ nhỏ nhất là 2 nên ƯCLN(90, 27) = 32 = 9
Do đó 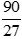 không là phân số tối giản.
không là phân số tối giản.
Ta có 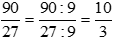 . Ta được
. Ta được 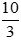 là phân số tối giản vì ƯCLN(10, 3) = 1.
là phân số tối giản vì ƯCLN(10, 3) = 1.
b) Ta có: 50 = 2.52 ; 125 = 53
+) Thừa số nguyên tố chung là: 5 với số mũ nhỏ nhất là 2 nên ƯCLN(50, 125) = 52 = 25
Do đó 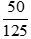 không là phân số tối giản
không là phân số tối giản
Ta có 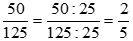 . Ta được
. Ta được 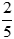 là phân số tối giản vì ƯCLN(2, 5) = 1.
là phân số tối giản vì ƯCLN(2, 5) = 1.
Bài tập
Bài 2.30 trang 48 Toán lớp 6 Tập 1:
Tìm tập hợp ước chung của:
a) 30 và 45;
b) 42 và 70.
Lời giải:
a) Phân tích các số 30 và 45 ra thừa số nguyên tố:
30 = 2.3.5; 45 = 32.5
+) Ta chọn ra các thừa số nguyên tố chung là: 3 và 5.
+) Số mũ nhỏ nhất của 3 là 1, số mũ nhỏ nhất của 5 là 1. Khi đó:
ƯCLN(30, 45) = 3.5 = 15. Ta được ƯC(30; 45) = Ư(15) = {1; 3; 5; 15}
Vậy ƯC(30; 45) = {1; 3; 5; 15}.
b) Phân tích các số 42 và 70 ra thừa số nguyên tố:
42 = 2.3.7; 70 = 2.5.7;
+) Ta chọn ra các thừa số nguyên tố chung là: 2 và 7.
+) Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 7 là 1. Khi đó:
ƯCLN(42, 70) = 2.7 = 14. Ta được ƯC(42; 70) = Ư(14) = {1; 2; 7; 14}
Vậy ƯC(42; 70) = {1; 2; 7; 14}.
Bài 2.31 trang 48 Toán lớp 6 Tập 1:
Tìm ƯCLN của hai số:
a) 40 và 70;
b) 55 và 77.
Lời giải:
a) Phân tích các số 40 và 70 ra thừa số nguyên tố ta được:
40 = 23.5; 70 = 2.5.7
Ta thấy 2 và 5 là các thừa số nguyên tố chung của 40 và 70. Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 5 là 1 nên ƯCLN(40, 70) = 2. 5 = 10
Vậy ƯCLN(40, 70) = 10.
b) Phân tích các số 55 và 77 ra thừa số nguyên tố ta được:
55 = 5. 11; 77 = 7. 11
Ta thấy 11 thừa số nguyên tố chung của 55 và 77. Số mũ nhỏ nhất của 11 là 1 nên ƯCLN(55, 77) = 11
Vậy ƯCLN(40, 70) = 11.
Bài 2.32 trang 48 Toán lớp 6 Tập 1:
Tìm ƯCLN của:
a) 22.5 và 2. 3. 5;
b) 24.3; 22.32.5 và 24.11
Lời giải:
a) 22.5 và 2. 3. 5
Ta thấy 2 và 5 là thừa số nguyên tố chung. Số mũ nhỏ nhất của 2 là 1 và số mũ nhỏ nhất của 5 là 1 nên
ƯCLN cần tìm là 2.5 = 10.
b) 24.3; 22.32.5 và 24.11
Ta thấy 2 là thừa số nguyên tố chung. Số mũ nhỏ nhất của 2 là 2 nên
ƯCLN cần tìm là 22 = 4
Bài 2.33 trang 48 Toán lớp 6 Tập 1:
Cho hai số a = 72 và b = 96
a) Phân tích a và b ra thừa số nguyên tố;
b) Tìm ƯCLN(a, b), rồi tìm ƯC(a, b).
Lời giải:
a) Phân tích a và b ra thừa số nguyên tố
Ta có:
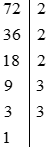
Do đó: a = 72 = 23.32.
Lại có:

Vậy b = 96 = 25.3.
b) Ta thấy 2 và 3 là các thừa số chung của 70 và 96. Số mũ nhỏ nhất của 2 là 3 và số mũ nhỏ nhất của 3 là 1 nên
ƯCLN(72; 96) = 23 . 3 = 24
ƯC(a, b) = Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}.
Bài 2.34 trang 48 Toán lớp 6 Tập 1:
Các phân số sau đã là phân số tối giản chưa? Nếu chưa, hãy rút gọn về phân số tối giản?
a) 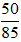 ; b)
; b) 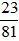 .
.
Lời giải:
a) Ta có:
50 = 2.52; 85 = 5.17
+) Thừa số nguyên tố chung là 5 với số mũ nhỏ nhất là 1 nên ƯCLN(50, 85) = 5.
Do đó 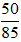 không là phân số tối giản.
không là phân số tối giản.
 . Ta được
. Ta được 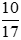 là phân số tối giản vì ƯCLN(10, 17) = 1.
là phân số tối giản vì ƯCLN(10, 17) = 1.
b) Ta có:
23 = 23; 81 = 34
Nên 23 và 81 không có thừa số nguyên tố chung nên ƯCLN(23, 81) = 1.
Do đó 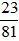 là phân số tối giản.
là phân số tối giản.
Bài 2.35 trang 48 Toán lớp 6 Tập 1: Hãy cho hai ví dụ về hai số có ƯCLN bằng 1 mà cả hai đều là hợp số.
Lời giải:
Có nhiều ví dụ về hai số có ƯCLN bằng 1 mà cả hai đều là hợp số, chẳng hạn ta có hai ví dụ sau:
+) 6 và 35
Vì 6 = 2.3; 35 = 5.7. Hai số này không có thừa số nguyên tố chung nên ƯCLN bằng 1 nhưng 6 chia hết cho 2 nên 6 là hợp số; 35 chia hết cho 5 nên 35 là hợp số.
+) 10 và 27
Vì 10 = 2.5; 27 = 33. Hai số này không có thừa số nguyên tố chung nên ƯCLN bằng 1 nhưng 10 chia hết cho 2 nên 10 là hợp số; 27 chia hết cho 3 nên 27 là hợp số.

Phần 2: Lý thuyết bài học
Với tóm tắt lý thuyết Toán lớp 6 Bài 11: Ước chung. Ước chung lớn nhất hay nhất, chi tiết sách Kết nối tri thức với cuộc sống sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 6.
A. Lý thuyết
1. Ước chung và ước chung lớn nhất
Ước chung của hai hay nhiều số là ước của tất cả các số đó.
Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.
Ta kí hiệu:
ƯC(a, b) là tập hợp các ước chung của a và b.
ƯCLN(a, b) là ước chung lớn nhất của a và b.
Ví dụ 1.
a) Tìm ước chung của 24 và 60.
b) Tìm ƯCLN (24; 60).
Lời giải
Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ư (30) = {1; 2; 3; 5; 6; 10; 15; 30}
a) ƯC(24; 30) = {1; 2; 3; 6}
b) ƯCLN(24; 30) = 6.
Nhận xét:
- Trong các số đã cho, nếu số nhỏ nhất là ước của các số còn lại thì ƯCLN của các số đã cho chính là số nhỏ nhất ấy.
Nếu a 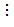 b thì ƯCLN(a, b) = b.
b thì ƯCLN(a, b) = b.
- Số 1 chỉ có 1 ước là 1. Do đó với mọi số tự nhiên a và b, ta có:
ƯCLN(a, 1) = 1; ƯCLN(a, b, 1) = 1.
Ví dụ 2.
a) Tìm ƯCLN(180, 18)
Vì 180  18 nên ƯCLN(180, 18) = 18.
18 nên ƯCLN(180, 18) = 18.
b) Tìm ƯCLN(13, 1)
Ta có: ƯCLN(13, 1) = 1.
2. Cách tìm ước chung lớn nhất
Các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1:
Bước 1: Phân tích các số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3. Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.
Ví dụ 3. Cách tìm ƯCLN(140, 168)
Ta có: 140 = 22.5.7; 168 = 23.3.7.
Các thừa số chung: 2, 7.
Vậy ƯCLN(140, 168) = 22.7 = 4.7 = 28.
3. Rút gọn về phân số tối giản
Vận dụng ƯCLN để rút gọn về phân số tối giản
Ta rút gọn phân số bằng cách chia cả tử và mẫu của phân số đó cho một ước chung khác 1 (nếu có).
Phân số 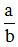 được gọi là phân số tối giản nếu a và b không có ước chung nào khác 1, nghĩa là ƯCLN(a, b) = 1.
được gọi là phân số tối giản nếu a và b không có ước chung nào khác 1, nghĩa là ƯCLN(a, b) = 1.
Ví dụ 4. Rút gọn các phân số sau về phân số tối giản
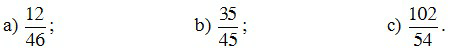
Lời giải
a) ƯCLN(12, 46) = 2.
Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 12 và 46, ta được:
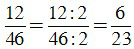 ;
;
b) ƯCLN(35,45) = 5.
Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 35 và 45, ta được:
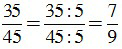 ;
;
c) ƯCLN(102, 54) = 6.
Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 102 và 54, ta được:
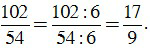
B. Bài tập
Bài 1. Cho hai số a = 132, b = 36.
a) Phân tích a và b ra thừa số nguyên tố.
b) Tìm ƯCLN(a, b) và ƯC(a, b).
Lời giải
a) 132 = 22.3.11; 36 = 22.32.
b) ƯCLN(132, 36) = 22.3 = 12.
ƯC(132, 36) = {1; 2; 3; 4; 6; 12}.
Bài 2. Các phân số sau đã tối giản chưa? Nếu chưa hãy rút gọn phân số đến phân số tối giản.

Lời giải
Tất cả các phân số đã cho đều chưa tối giản.
a) Vì 15050 nên ƯCLN(150, 50) = 50.
Để rút gọn phân số ta chia cả tử và mẫu cho 50, ta được:
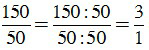 = 3
= 3
b) Ta có: 90 = 2.32.5, 27 = 33.
ƯCLN(90,27) =32 = 9.
Để rút gọn phân số ta chia cả tử và mẫu cho 9, ta được:
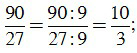
c) Ta có: 34 = 2.17, 255 = 3.5.17.
ƯCLN(34, 255) = 17.
Để rút gọn phân số ta chia cả tử và mẫu cho 17, ta được:
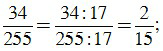
d) Ta có: 88 = 23.11, 121 = 112
ƯCLN(88, 121) = 11.
Để rút gọn phân số ta chia cả tử và mẫu cho 11, ta được:
 .
.

Phần 3: Bài tập trắc nghiệm
Với 21 bài tập trắc nghiệm Toán lớp 6 Bài 11: Ước chung. Ước chung lớn nhất có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức với cuộc sống sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 6.
I. Nhận biết
Câu 1. Cho tập Ư(8) = {1; 2; 4; 8} và Ư(20) = {1; 2; 4; 5; 10; 20}. Tập hợp ƯC(8; 20) là:
A. ƯC(8; 20) = {1; 2; 4}.
B. ƯC(8;20) = {1; 2}.
C. ƯC(8; 20) = {1;4}.
D. ƯC(8; 20) = {2;4}.
Lời giải
Các phần tử chung của tập Ư(8) và Ư(20) là: 1; 2; 4.
Do đó ƯC(8; 20) = {1;2;4}.
Đáp án: A
Câu 2. Chọn phát biểu đúng.
A. Ước chung của hai hay nhiều số chỉ có thể là số 1.
B. Ước chung lớn nhất của hai hay nhiều số là ước lớn nhất của số lớn nhất trong các số đó.
C. Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung cuả các số đó.
D. Cả A, B, C đều sai.
Lời giải
Ước chung của hai hay nhiều số là ước của tất cả các số đó, không nhất thiết là chỉ có số 1. Do đó A sai.
Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung cuả các số đó. Do đó B sai, C đúng, D sai.
Đáp án: C
Câu 3. Sắp xếp các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1 là:
1 – Chọn ra các thừa số nguyên tố chung.
2 – Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.
3 – Phân tích mỗi số ra thừa số nguyên tố.
A. 1 – 3 – 2;
B. 1 – 2 – 3;
C. 3 – 2 – 1;
D. 3 – 1 – 2;
Lời giải
Các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1 là:
3 – Phân tích mỗi số ra thừa số nguyên tố.
1 – Chọn ra các thừa số nguyên tố chung.
2 – Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.
Thứ tự đúng là: 3 – 1 – 2.
Đáp án: D
Câu 4. Tìm ƯCLN(90; 10)
A. ƯCLN(90; 10) = 10;
B. ƯCLN(90; 10) = 5;
C. ƯCLN(90; 10) = 90;
D. ƯCLN(90;10) = 1.
Lời giải
Vì 90 = 9.10 nên 90 chia hết cho 10. Do đó ƯCLN(90; 10) = 10.
Đáp án: A
Câu 5. Phân số 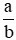 được gọi là phân số tối giản khi:
được gọi là phân số tối giản khi:
A. a và b không có ước chung nào khác 1.
B. a và b có ƯCLN(a, b) = 1.
C. Cả A và B đều đúng.
D. Cả A và B đều sai.
Lời giải
Phân số 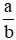 được gọi là phân số tối giản nếu a và b không có ước chung nào khác 1, nghĩa là ƯCLN(a, b) = 1.
được gọi là phân số tối giản nếu a và b không có ước chung nào khác 1, nghĩa là ƯCLN(a, b) = 1.
Đáp án: C
Câu 6. Cho tập ƯC(24; 28) = {1; 2; 4}. Vậy ƯCLN(24; 28) là:
A. 1;
B. 2;
C. 4;
D.24.
Lời giải
Tập ƯC(24; 28) = {1; 2; 4}.
Mà 4 là số lớn nhất trong tập này nên ƯCLN(24, 28) = 4.
Đáp án: C
Câu 7. Tìm ƯCLN(72, 63, 1):
A. 63;
B. 72;
C. 9;
D. 1.
Lời giải
Ta có ƯCLN(a, b, 1) = 1 với a, b là các số tự nhiên.
Vậy ƯCLN(72, 63, 1) = 1.
Đáp án: D
Câu 8. Muốn tìm tập hợp ước chung chung của hai hay nhiều số tự nhiên, ta thực hiện:
A. Tìm ƯCLN của các số đó. Khi đó tập hợp ước chung của các số đó chính là tập hợp ước của ƯCLN.
B. Viết tập hợp các ước của các số đó ra. Tìm trong số đó các phần tử chung. Tập các phần tử đó chính là tập hợp ước chung của các số đó.
C. Cả A và B đều sai.
D. Cả A và B đều đúng.
Lời giải
Muốn tìm tập hợp ước chung chung của hai hay nhiều số tự nhiên, ta có hai cách để tìm như sau:
Cách 1.
- Tìm ƯCLN của các số đó.
- Tìm các ước của ƯCLN đó.
- Kết luận tập hợp ƯC là tập các ước của ƯCLN.
Cách 2.
- Liệt kê tập hợp ước của các số.
- Tìm các phần tử chung của các tập hợp đó.
- Tập hợp ƯC là tập các phần tử chung đó.
Vậy cả A và B đều đúng.
Đáp án: D
Câu 9. Nếu 9 là số lớn nhất sao cho a ⋮ 9 và a ⋮ 9 thì 9 là ………… của a và b. Chọn câu trả lời đúng nhất.
A. ước;
B. ước chung;
C. ước chung lớn nhất;
D. bội.
Lời giải
Nếu 9 là số lớn nhất sao cho a ⋮ 9 và b ⋮ 9 thì 9 là ước chung lớn nhất của a và b.
Đáp án: C
Câu 10. Nếu a ⋮ 7 và a ⋮ 7 thì 7 là ……………… của a và b.
A. ước
B. ước chung;
C. ước chung lớn nhất;
D. bội.
Lời giải
Nếu a ⋮ 7 và b ⋮ 7 thì 7 là ước chung của a và b.
Đáp án: B
II. Thông hiểu
Câu 1. Tìm ƯCLN(36, 84)
A. 2;
D. 4;
C. 3;
D. 12.
Lời giải
Ta có: 36 = 22.32; 84 = 22.3.7.
Tích các nhân tử chung với số mũ nhỏ nhất là: 22.3.
ƯCLN(36, 84) = 22.3 = 12.
Đáp án: D
Câu 2. Rút gọn phân số 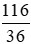 về phân số tối giản:
về phân số tối giản:
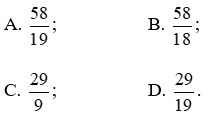
Lời giải
Ta có: 114 = 22.29; 36 = 22.32.
ƯCLN(114, 36) = 22 = 4.
Khi đó: 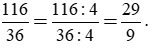
Đáp án: C
Câu 3. Biết ƯCLN(75, 105) = 15. Hãy tìm ƯC(15, 105).
A. ƯC(15, 105) = Ư(15) = {1; 3; 5}.
B. ƯC(15, 105) = Ư(15) = {1; 5; 15}.
C. ƯC(15, 105) = Ư(15) = {1; 3; 5;15}.
D. ƯC(15, 105) = Ư(15) = {1; 15}.
Lời giải
Lần lượt chia 15 cho các số tự nhiên từ 1 đến 15 ta thấy 15 chia hết cho các số 1; 3; 5 và 15.
Suy ra Ư(15) = {1; 3; 5;15}.
Ta có: ƯC(15, 105) = Ư(15) = {1; 3; 5; 15}.
Đáp án: C
Câu 4. Tìm ƯCLN(56, 140, 168).
A. 56;
B. 28;
C. 7;
D. 4.
Lời giải
Ta có: 56 = 23.7; 140 = 22.5.7; 168 = 23.3.7.
Tích các thừa số chung với số mũ nhỏ nhất là: 22.7.
Vậy ƯCLN(56, 140, 168) = 22.7 = 28.
Đáp án: B
Câu 5. Cho các phân số sau: 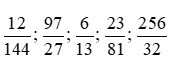 . Có bao nhiêu phân số tối giản trong các phân số trên.
. Có bao nhiêu phân số tối giản trong các phân số trên.
A. 0;
B. 1;
C. 2;
D. 3.
Lời giải
Ta có:
+) Xét phân số: 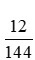
Ta có 12 = 22.3; 144 = 24.32 nên Ư CLN(12, 144) = 22.3 = 12 nên phân số này không tối giản.
+) Xét phân số: 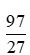
Vì 97 là số nguyên tố, 27 = 33 nên ƯCLN(97, 27) = 1.
Do đó phân số này tối giản.
+) Xét phân số: 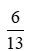
Ta có 6 = 2.3, 13 = 13 (do 13 là số nguyên tố) nên ƯCLN(6, 13) = 1.
Do đó đây là phân số tối giản.
+) Xét phân số: 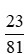
Ta có: 23 = 23, 81 = 34 nên ƯCLN(23, 81) = 1.
Do đó đây là phân số tối giản.
+) Xét phân số 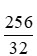
Ta có 256 = 28; 32 = 25 nên Ư CLN(256, 32) = 25 = 32.
Do đó đây không phải phân số tối giản.
Vậy có 3 phân số tối giản trong dãy phân số đã cho.
Đáp án: D
Câu 6. Tìm số tự nhiên a lớn nhất sao cho 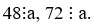
A. a = 12;
B. a = 6;
C. 24;
D. 48.
Lời giải
Ta có 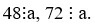 nên a là ước chung của 48 và 72
nên a là ước chung của 48 và 72
Mà a lớn nhất nên a chính là ƯCLN(48, 72)
Ta có 48 = 24.3; 72 = 23.32.
ƯCLN(48, 72) = 23.3 = 24.
Vậy a = 24.
Đáp án: C
Câu 7. Phát biểu nào dưới đây là sai:
A. ƯCLN(35, 21) = 7.
B. ƯCLN(72, 90) = 18.
C. Cả A và B đều đúng.
D. Cả A và B đều sai.
Lời giải
+) Ta có 35 = 5.7, 21 = 3.7
Nên ƯCLN(35, 21) = 7. Do đó A đúng.
+) Ta có 72 = 23.32; 90 = 2.32.5.
ƯCLN(72, 90) = 2.32 = 18. Do đó B đúng.
Suy ra C đúng.
Vậy D sai.
Đáp án: D
III. Vận dụng
Câu 1. Tuấn và Hà mỗi người mua một số hộp bút chì màu, trong mỗi hộp đều có từ hai chiếc bút trở lên và số bút trong mỗi hộp là như nhau. Tính ra Tuấn mua 25 bút, Hà mua 20 bút. Hỏi mỗi hộp bút chì màu có bao nhiêu chiếc.
A. 1;
B. 20;
C. 25;
D. 5.
Lời giải
Số bút chì trong mỗi hộp là như nhau nên số bút trong mỗi hộp chính là ước chung của 25 và 20.
Ta có 25 = 52; 20 = 22.5
Khi đó ƯCLN(25, 20) = 5.
ƯC(25, 20) = Ư(5) = {1;5}.
Mà mỗi hộp đều có từ hai chiếc bút trở lên nên số bút trong mỗi hộp là 5.
Đáp án: D
Câu 2. Tìm tất cả các số tự nhiên khác 0, không vượt quá 60 sao cho ƯCLN của hai số đó là 17.
A. 17; 34 và 51.
B. 17; 34 và 41.
C. 17 và 51.
D. 17 và 34.
Lời giải
Các số tự nhiên có ƯCLN là 17 nên các số đó là bội của 17.
Muốn tìm bội của 17, ta nhân lần lượt 17 với các số tự nhiên 0; 1; 2; 3; 4; 5; 6; …
B(17) = {0; 17; 34; 51; 68; …}.
Mà các số tự nhiên cần tìm khác 0 và không vượt quá 60 nên các số đó là: 17; 34 và 51.
Đáp án: A
Câu 3. Một số bằng tổng các ước của nó (không kể chính nó) gọi là số hoàn hảo. Chẳng hạn, các ước của 6 (không kể chính nó) là 1; 2; 3 ta có 1 + 2 + 3 = 6. Vậy 6 là số hoàn hảo. Hãy chỉ ra trong các số 10; 28; 49 số nào là số hoàn hảo.
A. 10;
B. 28;
C. 49;
D. 10; 28 và 49.
Lời giải
+) Lấy 10 chia cho các số tự nhiên từ 1 đến 10 ta thấy 10 chia hết cho 1; 2; 5; 10.
Các ước của 10 không kể chính nó là: 1; 2 và 5.
Ta có: 1 + 2 + 5 = 8 (khác 10).
Vậy 10 không phải là số hoàn hảo.
+) Lấy 28 chia cho các số tự nhiên từ 1 đến 28 ta thấy 28 chia hết cho 1; 2; 4; 7; 14; 28.
Các ước của 28 không kể chính nó là: 1; 2; 4; 7; 14.
Ta có: 1 + 2 + 4 + 7 + 14 = 28.
Vậy 28 là số hoàn hảo.
+) Lấy 49 chia cho các số tự nhiên từ 1 đến 49 ta thấy 49 chia hết cho 1; 7; 49.
Các ước của 49 không kể chính nó là: 1; 7.
Ta có 1 + 7 = 8 (khác 49)
Vậy 49 không phải số hoàn hảo.
Đáp án: B


