Bài 13: Tập hợp các số nguyên
Bài 13: Tập hợp các số nguyên
Bài 13: Tập hợp các số nguyên
Phần 1: Giải Sách Giáo Khoa
Trả lời câu hỏi giữa bài
Hoạt động 1 trang 58 Toán lớp 6 Tập 1: Số - 3 đọc là “âm 3”. Tương tự, hãy đọc các số âm mà em thấy trên bản đồ thời tiết (H.3.1) và trên chiếc nhiệt kế (H.3.2)

Lời giải:
* Trên hình 3.1
+) Số -2 đọc là “âm 2”
+) Số -8 đọc là “âm 8”
+) Số -11 đọc là “âm 11”
*Trên hình 3.2
+) Số -20 đọc là “âm 20”
+) Số -20 đọc là “âm 20”
+) Số -30 đọc là “âm 30”
Hoạt động 2 trang 58 Toán lớp 6 Tập 1: Bằng cách sử dụng dấu " –", hãy viết các số âm được nói đến trong Hình 3.3.

Lời giải:
+) Âm 65 viết là -65
+) Âm 30 viết là -30
Luyện tập 1 trang 58 Toán lớp 6 Tập 1:
a) Viết ba số nguyên dương và ba số nguyên âm;
b) Đọc các số mà em đã viết.
Lời giải:
a) Ba số nguyên dương là: 5; 6; 9 và ba số nguyên âm là: -1; -10; -15
b) Đọc các số đã viết:
+) 5: Năm; 6: Sáu; 9: Chín
+) - 1: âm 1; - 10: âm 10; - 15: âm 15
Câu hỏi 1 trang 59 Toán lớp 6 Tập 1: Khi được hỏi còn tiền không, Nam hóm hỉnh đáp: “Mình còn âm mười nghìn đồng”. Em hiểu câu nói đó của Nam có nghĩa là gì?
Lời giải:
Khi được hỏi còn tiền không, Nam hóm hỉnh đáp: “Mình còn âm mười nghìn đồng”. Ta hiểu câu nói đó của Nam là Nam đang nợ ai đó 10 nghìn đồng.
Vận dụng 1 trang 59 Toán lớp 6 Tập 1:
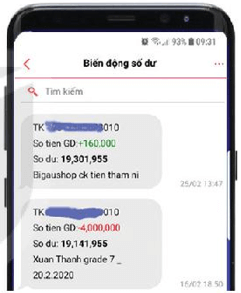
Ông M nhận được hai tin nhắn từ một ngân hàng với nội dung như sau:
1. “Tài khoản … 010. Số tiền giao dịch: + 160 000. …”
2. “Tài khoản … 010. Số tiền giao dịch: - 4 000 000. …”
Em hãy giải thích ý nghĩa của số âm và số dương trong mỗi tin nhắn trên.
Lời giải:
1. Số dương trong tin nhắn trên tức là tài khoản của ông được cộng thêm tiền. Cụ thể là được cộng 160 000 đồng.
2. Số âm trong tin nhắn trên tức là tài khoản của ông bị trừ tiền. Cụ thể là bị trừ 4 000 000 đồng.
Câu hỏi 2 trang 60 Toán lớp 6 Tập 1:
Trên trục số, mỗi điểm sau nằm cách gốc O bao nhiêu đơn vị?
a) Điểm 2; b) Điểm – 4.
Lời giải:
Ta có trục số sau:

Dựa vào trục số:
a) Điểm 2 cách gốc O một khoảng là 2 đơn vị
b) Điểm -4 cách gốc O một khoảng là 4 đơn vị.
Luyện tập 2 trang 60 Toán lớp 6 Tập 1:
Xuất phát từ gốc O, ta sẽ đi đến điểm nào nếu:
a) Di chuyển 5 đơn vị theo chiều dương?
b) Di chuyển 5 đơn vị theo chiều âm?
Lời giải:

Dựa vào trục số: Xuất phát từ điểm gốc O
a) Di chuyển 5 đơn vị theo chiều dương ta sẽ đi đến điểm 5.
b) Di chuyển 5 đơn vị theo chiều âm ta sẽ đi đến điểm -5.
Hoạt động 3 trang 60 Toán lớp 6 Tập 1:
Trên trục số các số nguyên âm nằm trước hay sau gốc O? Từ đó em hãy sắp xếp ba số 0, 1 và – 1 theo thứ tự từ nhỏ đến lớn.
Lời giải:

Trên trục số, các số nguyên âm nằm trước gốc O.
Vì -1 là số nguyên âm nên -1 < 0 mà 0 < 1 nên -1 < 0 <1
Vậy sắp xếp thứ tự từ nhỏ đến lớn là: -1; 0; 1.
Hoạt động 4 trang 60 Toán lớp 6 Tập 1:
Quan sát trên trục số (H.3.6), ta thấy:
3 < 5 nhưng - 3 > - 5
4 > 1 nhưng – 4 < - 1
Theo em, trong hai số - 12 và – 15, số nào lớn hơn?

Lời giải:
Theo em vì 12 < 15 nên -12 > -15.
Luyện tập 3 trang 60 Toán lớp 6 Tập 1:
1. Sắp xếp các số sau theo thứ tự tăng dần: 2; - 4; 0; 5; - 11; - 3; 9.
2. Trong tập {x ∈ Z| - 5 < x ≤ 2}, những số nào lớn hơn – 1?
Lời giải:
1. +) Các số nguyên âm là: -4; -11; -3
Vì 11 > 4 > 3 nên -11 < -4 < -3 < 0 (1)
+) Các số nguyên dương là: 2; 5; 9
Ta có: 0 < 2 < 5 < 9 (2)
Từ (1) và (2) ta được: -11 < -4 < -3 < 0 < 2 < 5 < 9
Sắp xếp các số theo thứ tự tăng dần là: -11; -4; -3; 0; 2; 5; 9
2. Vì x là số nguyên lớn hơn - 5 và nhỏ hơn hoặc bằng 2 nên x là: -4; -3; -2; -1; 0; 1; 2
Các số nguyên lớn hơn -1 trong tập trên là: 0; 1; 2
Vậy x ∈ {0;1;2}.
Vận dụng 2 trang 60 Toán lớp 6 Tập 1:
Nhiệt độ trung bình vào tháng Giêng của ba thành phố lớn của nước Nga được ghi lại trong bảng bên (theo Wikipedia).
Hãy sắp xếp ba thành phố trên theo thứ tự giảm dần về nhiệt độ. Theo em thời tiết ở nơi nào lạnh hơn cả?

Lời giải:
Vì 12 > 9 > 8 nên -12 < -9 < -8
Sắp xếp ba thành phố theo thứ tự giảm dần về nhiệt độ: Saint Peterburg, Moscow, Vladivostok.
Do đó thời tiết ở Vladivostok lạnh hơn cả.
Tranh luận trang 61 Toán lớp 6 Tập 1:
Giả sử một con kiến bò trên sợi dây (giống như một trục số). Nếu nó đi được 4 đơn vị theo chiều dương, ta nói kiến bò được 4 đơn vị; nếu nó đi được 4 đơn vị nhưng theo chiều âm, ta nói kiến bò được – 4 đơn vị.
a) Em hiểu thế nào nào nếu nói: “Kiến A bò được 12 đơn vị” và “Kiến B bò được – 15 đơn vị”?
b) Từ nhận xét rằng 12 > - 15, An kết luận: kiến A bò được quãng đường dài hơn kiến B. Em có đồng ý với An không?
Lời giải:
a) Nếu nói: “Kiến A bò được 12 đơn vị” được hiểu là kiến A bò được 12 đơn vị theo chiều dương.
“Kiến bò được – 15 đơn vị” được hiểu là kiến B bò được 15 đơn vị theo chiều âm.
b) Từ nhận xét rằng 12 > - 15, An kết luận: Kiến A bò được quãng đường dài hơn kiến B. Em không đồng ý với An vì:
Vì độ dài quãng đường không âm nên:
Kiến A bò được quãng đường là 12 đơn vị, kiến B bò được quãng đường là 15 đơn vị. Mà 12 < 15 nên kiến A bò được quãng đường ngắn hơn kiến B.
Bài tập
Bài 3.1 trang 61 Toán lớp 6 Tập 1: Mỗi nhiệt kế dưới đây chỉ bao nhiêu độ C?

Lời giải:
Nhiệt độ mỗi nhiệt kế chỉ lần lượt là: -7oC; 31oC ; 0oC; -22oC
Bài 3.2 trang 61 Toán lớp 6 Tập 1:
Hãy sử dụng số nguyên âm để diễn tả lại ý nghĩa của các câu sau đây:
a) Độ sâu trung bình của vịnh Thái Lan khoảng 45 m và độ sâu lớn nhất là 80 m dưới mực nước biển.
b) Mùa đông ở Siberia (Nga) dài và khắc nghiệt, với nhiệt độ trung bình tháng 1 là 25oC dưới 0oC.
c) Năm 2012, núi lửa Havre (Bắc New Zealand) phun ra cột tro từ độ sâu 700 m dưới mực nước biển.
Lời giải:
a) Độ cao trung bình của vịnh Thái Lan khoảng - 45m và độ cao thấp nhất là - 80m.
b) Mùa đông ở Siberia (Nga) dài và khắc nghiệt với nhiệt độ trung bình tháng 1 là -25oC.
c) Năm 2012, núi lửa Harve (Bắc New Zealand) phun ra cột tro từ độ cao -700m.
Bài 3.3 trang 61 Toán lớp 6 Tập 1:
Em hiểu ý nghĩa của mỗi câu sau như thế nào (diễn tả bằng một câu không sử dụng số âm)
a) Khi máy bay ở độ cao 10 000 m, nhiệt độ bên ngoài có thể xuống đến -50oC ;
b) Cá voi xanh có thể lặn được – 2 500 m.
Lời giải:
a) Khi máy bay ở độ cao 10 000 m, nhiệt độ bên ngoài có thể xuống đến dưới 0oC
b) Cá voi xanh có thể lặn được độ sâu 2 500m dưới mực nước biển.
Bài 3.4 trang 61 Toán lớp 6 Tập 1: Hãy biểu diễn các số sau đây trên cùng một trục số: 3; - 3; - 5; 6; - 4; 4.
Lời giải:
Biểu diễn các số sau đây trên cùng một trục số: 3; - 3; - 5; 6; - 4; 4.
+) Các số nguyên dương nằm bên phải số 0 là: 3; 4; 6
+) Các số nguyên âm nằm bên trái số 0 là: -3; -4; -5

Bài 3.5 trang 61 Toán lớp 6 Tập 1: Các điểm A, B, C, D và E trong hình dưới đây biểu diễn những số nào?
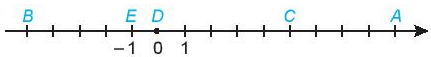
Lời giải:
Dựa vào hình vẽ ta thấy: Điểm D biểu diễn số 0; điểm E biểu diễn số -1
Xuất phát từ điểm E, di chuyển điểm E sang trái 4 đơn vị ta được điểm B nên điểm B biểu diễn số -5.
Xuất phát từ điểm D, di chuyển điểm D sang phải 5 đơn vị ta được điểm C nên điểm C biểu diễn số 5.
Xuất phát từ điểm C, di chuyển điểm C sang phải 4 đơn vị ta được điểm A nên điểm A biểu diễn số 9.
Vậy các điểm A, B, C, D, E lần lượt biểu diễn các số: 9; -5; 5; 0; -1.
Bài 3.6 trang 61 Toán lớp 6 Tập 1:
Hãy sắp xếp các số sau theo thứ tự tăng dần
-3; + 4; 7; - 7; 0; - 1; + 15; - 8; 25.
Lời giải:
+) Các số nguyên âm là: -3; -7; -1; -8
Vì 8 > 7 > 3 > 1 nên -8 < -7 < -3 < -1 < 0 (1)
+) Các số nguyên dương là: +4; 7; 15; 25
Ta có: 0 < 4 < 7 < 15 < 25 (2)
Từ (1) và (2) ta được: -8 < -7 < -3 < -1 < 0 < 4 < 7 < 15 < 25
Bài 3.7 trang 61 Toán lớp 6 Tập 1:
So sánh hai số
a) – 39 và – 54;
b) – 3 179 và – 3 279.
Lời giải:
a) Vì 39 < 54 nên -39 > -54;
b) Vì 3 179 < 3 279 nên – 3 179 > – 3 279.
Bài 3.8 trang 61 Toán lớp 6 Tập 1: Liệt kê các phần tử của mỗi tập hợp sau:
a) {x ∈ Z|-2 ≤ X < 4}
b) {x ∈ Z|-2 < X ≤ 4}
Lời giải:
a) Các số nguyên thỏa mãn lớn hơn hoặc bằng -2 và nhỏ hơn 4 là: -2; -1; 0; 1; 2; 3
Do đó: A = {-2; -1; 0; 1; 2; 3} .
b) Các số nguyên thỏa mãn lớn hơn -2 và nhỏ hơn hoặc bằng 4 là: -1; 0; 1; 2; 3; 4
Do đó: B = { -1; 0; 1; 2; 3; 4}.

Phần 2: Lý thuyết bài học
Với tóm tắt lý thuyết Toán lớp 6 Bài 13: Tập hợp các số nguyên hay nhất, chi tiết sách Kết nối tri thức với cuộc sống sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 6.
A. Lý thuyết
1. Làm quen với số nguyên âm
- Các số tự nhiên (khác 0) 1; 2; 3; 4; … còn được gọi là các số nguyên dương.
- Các số - 1; -2; -3; … gọi là các số nguyên âm.
- Tập hợp gồm các số nguyên âm, số 0 và số nguyên dương gọi là tập hợp số nguyên.
Z = {...; -3; -3; -3; 0; 1; 2; 3;...}.
Chú ý:
Số 0 không là số nguyên âm, cũng không phải là số nguyên dương.
Đôi khi ta còn viết thêm dấu “+” ngay trước một số nguyên dương. Chẳng hạn số 6 còn được viết là +6 (đọc là “dương sáu”).
Ví dụ 1. Các số nguyên nào biểu diễn các đại lượng sau:
a) Đỉnh núi Phan – xi – păng cao 3 147, 3m;
b) Độ sâu của đáy sông Sài Gòn là 20m;
c) Bác An đang nợ 2 triệu đồng.
Lời giải
a) Độ cao củ đỉnh núi Phan – xi – păng được biểu diễn là: 3 147, 3m.
b) Độ sâu của đáy sông Sài Gòn được biểu diễn là: -20 m.
c) Số tiền nợ của bác An được biểu diễn là: - 2 (triệu đồng).
2. Thứ tự trong tập số nguyên
Trục số:
Ta biểu diễn các số 0; 1; 2; 3; 4; 5 … và các số nguyên âm -1; -2; -3; 4; 5… như sau:
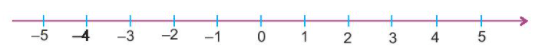
+ Chiều từ trái sang phải là chiều dương, chiều ngược lại là chiều âm.
+ Điểm biểu diễn số nguyên a được gọi là điểm a.
+ Cho hai số nguyên a và b. Trên trục số, nếu điểm a nằm trước điểm b thì số a nhỏ hơn số b, kí hiệu a < b.
Ví dụ 2. Các điểm A, B, C, D và E trong hình biểu diễn những số nào?

Lời giải
Điểm A cách điểm 0 năm đơn vị về bên phải nên A biểu diễn cho số 5;
Điểm C cách điểm 0 bảy đơn vị về bên phải nên C biểu diễn cho số 7;
Điểm B cách điểm 0 bốn đơn vị về bên trái nên B biểu diễn cho số -4;
Điểm E biểu diễn cho điểm – 1;
Điểm D biểu diễn cho điểm 0;
So sánh hai nguyên:
Mọi số nguyên âm đều nhỏ hơn 0, do đó nhỏ hơn mọi số nguyên dương.
Nếu a, b là hai số nguyên dương và a > b thì – a < - b.
Ví dụ 2. Sắp xếp các số sau theo thứ tự tăng dần:
- 3; 4; -9; 0; -12; 2; 15; 1.
Lời giải
Các số đã cho được sắp xếp theo thứ tự tăng dần là:
-12; -9; -3; 0; 1; 2; 4; 15.
B. Bài tập
Bài 1. Liệt kê các phần tử của mỗi tập hợp sau:
a) B = {x ∈ Z | -3 ≤ x ≤ 4} ;
b) B = {x ∈ Z | -2 ≤ x ≤ 0}.
Lời giải
a) A = {-3; -2; -1; 0; 1; 2; 3}.
b) B = {-2; -1; 0}.
Bài 2. So sánh hai số:
a) -49 và -38; b) -1379 và – 2379.
Lời giải
a) Vì 49 > 38 nên -49 < -38.
b) Vì 2379 > 1379 nên -2379 < -1379.
Bài 3. Hãy sử dụng số nguyên âm để diễn tả lại ý nghĩa của các câu sau:
a) Mùa đông ở Siberia (Nga) dài và khắc nghiệt, với nhiệt độ trung bình tháng 1 là 25oC dưới 0oC .
b) Cá voi xanh có thể lặn sâu 2500m có với mực nước biển.
Lời giải
a) Nhiệt độ trung bình tháng 1 của Siberia (Nga) được biểu diễn là: -25oC .
b) Độ sâu mà Cá voi xanh có thể lặn được biểu diễn là: – 2500 m.

Phần 3: Bài tập trắc nghiệm
Với 15 bài tập trắc nghiệm Toán lớp 6 Bài 13: Tập hợp các số nguyên có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức với cuộc sống sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 6.
I. Nhận biết
Câu 1. Kết luận nào sau đây là đúng.
A. Số 0 vừa là số nguyên dương, vừa là số nguyên âm.
B. Số 1 là số nguyên dương.
C. Số - 3 đọc là trừ ba.
B. Số - 25 là số nguyên dương.
Lời giải
Số 0 không phải số nguyên dương cũng không phải số nguyên âm nên A sai.
Số 1 là số nguyên dương nên B đúng.
Số - 3 đọc là âm ba nên C sai.
Số -25 là số nguyên âm nên D sai.
Đáp án: B
Câu 2. Ông M đang nợ ngân hàng 200 triệu đồng. Số nguyên nào sau đây biểu diễn số tiền ông M đang có?
A. – 200;
B. 200;
C. 200 000 000;
D. – 200 000 000.
Lời giải Ông M đang nợ ngân hàng 200 000 000 đồng nên số nguyên biểu diễn số tiền ông đang có là – 200 000 000 (đồng).
Đáp án: D
Câu 3. Cho bảng nhiệt độ của các thành phố lớn của nước ta:
|
Thành phố |
Hà Nội |
Huế |
Phan Thiết |
Hồ Chí Minh |
|
Nhiệt độ |
340C |
330C |
310C |
320C |
Hỏi nhiệt độ của tỉnh thành nào thấp nhất?
A. Hà Nội;
B. Huế;
C. Phan Thiết;
D. Hồ Chí Minh.
Câu 4. Hai nhiệt kế dưới đây chỉ bao nhiêu độ C?
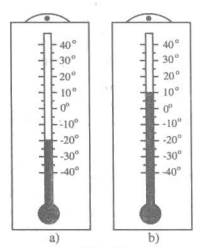
A. Nhiệt kế a chỉ 20 độ C, nhiệt kế b chỉ 10 độ C.
B. Nhiệt kế a chỉ - 20 độ C, nhiệt kế b chỉ - 10 độ C.
C. Nhiệt kế a chỉ - 20 độ C, nhiệt kế b chỉ 10 độ C.
D Nhiệt kế a chỉ 20 độ C, nhiệt kế b chỉ - 10 độ C.
Lời giải
Dựa vào quan sát hình vẽ, ta thấy:
Hình a, nhiệt kế có mức thủy ngân dưới mức 0 độ C nên nhiệt kế chỉ - 20 độ C.
Hình b, nhiệt kế có mức thủy ngân trên mức 0 độ C nên nhiệt kế chỉ 10 độ C.
Đáp án: C
Câu 5. Cho hình vẽ sau và cho biết điểm M biểu diễn cho số nguyên nào?

A. -7;
B. - 2;
C. 1;
D. 4.
Lời giải Quan sát trục số: Điểm M nằm ở bên trái điểm 0 trên trục số và cách 0 hai đơn vị nên điểm M biểu diễn cho số nguyên -2.
Đáp án: B
Câu 6. Cách đọc số - 12 304 nào sau đây là đúng.
A. âm mười hai nghìn ba trăm linh tư.
B. Trừ mười hai nghìn ba trăm linh tư.
C. Mười hai nghìn ba trăm linh tư.
D. Âm mười hai ba trăm không bốn.
Lời giải Cách đọc số - 12 304 là: âm mười hai nghìn ba trăm linh tư.
Đáp án: A
Câu 7. Tập hợp số nguyên được kí hiệu là:
A. N;
B. N*;
C. Z;
D. Q.
Lời giải Tập hợp số nguyên được kí hiệu là: Z.
Đáp án: C
Câu 8. Hình vẽ nào sau đây điểm N biểu diễn đúng điểm – 6 trên trục số?
A.

B.

C.

D.

Lời giải
Hình vẽ điểm N biểu diễn cho điểm – 6 trên trục số là:

Đáp án: B
Câu 9. Phát biểu nào sau đây là sai:
A. – 54 < - 34;
B. – 3 179 < - 3 279;
C. 87 < 97.
D. 1 197 > 1 179.
Lời giải
Vì 54 > 34 nên – 54 < - 34. Do đó A đúng.
Vì 3 179 < 3 279 nên – 3 179 > - 3 279. Do đó B sai.
Trên trục số 87 nằm bên trái 97 nên 87 < 97. Do đó C đúng.
Trên trục số 1 179 nằm bên trái 1 197 nên 1 179 < 1 197. Do đó D đúng.
Đáp án: B
Câu 10. Số nguyên âm có hai chữ số nhỏ nhất là:
A. - 99;
B. - 10;
C. – 11;
D. – 98.
Lời giải Số nguyên dương có hai chữ số lớn nhất là 99 thì số nguyên âm có hai chữ số nhỏ nhất là -99.
Đáp án: A
II. Thông hiểu
Câu 1. Hãy sắp xếp số sau theo thứ tự tăng dần: -3; +4; 7; -7; 0; -1.
A. – 7; - 3 ; - 1; 0 ; + 4 ; 7.
B. 7; +4; 0; -1; -3; -7.
C.7; -7; +4; -3; -1; 0.
D. 0; -1; -3; +4; - 7; 7.
Lời giải
Ta chia làm 3 nhóm:
+) Nhóm 1 gồm các số nguyên âm: -3; -7; -1.
+) Nhóm 2 gồm các số nguyên: 0; +4; 7.
Xét nhóm 1:
Ta có số đối của -3 là 3;
Số đối của – 7 là 7;
Số đối của -1 là 1;
Vì 1 < 3 < 7 nên - 7 < - 3 < - 1.
Xét nhóm 2: ta có 0 < 4 < 7.
Mà các số nguyên âm luôn nhỏ hơn 0 nên ta có: - 7 < - 3 < - 1 < 0 < 4 < 7.
Các số được sắp theo thứ tự tăng dần là: – 7; - 3 ; - 1; 0 ; + 4 ; 7.
Đáp án: A
Câu 2. Liệt kê các phần tử của mỗi tập hợp: P = {x ∈ ℕ | -2 ≤ x < 4}.
A. P = { -2; -1; 0; 1; 2; 3; 4}.
B. P = {-1; 0; 1; 2; 3; 4}.
C. P = {-1; 0; 1; 2; 3}.
D. P = {-2; -1; 0; 1; 2; 3}.
Lời giải
Các số tự nhiên thỏa mãn lớn hơn hoặc bằng – 2 nhỏ hơn 4 là: -2; -1; 0; 1; 2; 3.
Vậy P = {-2; -1; 0; 1; 2; 3}.
Đáp án: D
Câu 3. Cho tập hợp K = {0; 1; 2; 4; 5; 7; 9}. Tập hợp H là tập hợp gồm các số đối của phần tử của tập hợp K.
A. K = {0; -1; -2; -4; -5; -7; -9}.
B. K = {- 0; -1; -2; -4; -5; -7; -9}.
C. K = {-1; -2; -4; -5; -7; -9}.
D. K = { -1; -2; -4; -5; -7; -9; 0; 1; 2; 4; 5; 7; 9}.
Lời giải
Số đối của 0 là 0;
Số đối của 1 là -1;
Số đối của 2 là – 2;
Số đối của 4 là -4;
Số đối của 5 là -5;
Số đối của 7 là -7;
Số đối của 9 là -9.
Vậy tập hợp K = {0; -1; -2; -4; -5; -7; -9}.
Đáp án: A
Câu 4. Cho tập hợp J = {x ∈ ℤ | -13 < x < -12}. Phát biểu nào dưới đây là đúng.
A. Tập hợp J có 1 phần tử.
B. Tập hợp J có 2 phần tử.
C. Tập hợp J có 3 phần tử.
D. Tập hợp J có 0 phần tử.
Lời giải
Không tồn tại số nguyên nào lớn hơn -13 và nhỏ hơn -12.
Vậy J có 0 phần tử.
Đáp án: D
Câu 5. Tìm các số nguyên x thỏa mãn – 12 < x < 13. Có bao nhiêu số nguyên như vậy?
A. 23;
B. 24;
C. 25;
D. 26.
Lời giải
Các số nguyên thỏa mãn – 12 < x < 13 là: -11; -10; -9; -8; -7; -6; -5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12.
Tất cả có 24 số thỏa mãn.
Đáp án: B


