Bài 3: Thứ tự trong tập hợp các số tự nhiên

Phần 1: Giải Sách Giáo Khoa

Trả lời câu hỏi giữa bài

Mở đầu trang 13 Toán lớp 6 Tập 1: Mỗi khi có trận bóng đá hay, người dân lại xếp hàng dài chờ mua vẽ. Nhìn dòng người xếp hàng một, rất dài, Hà tự hỏi: dòng người xếp hàng ấy và dãy số tự nhiên đang học có gì giống nhau nhỉ?

Lời giải:

Ta nhận thấy dòng người đang xếp hàng dài ấy giống với thứ tự trong tập hợp số tự nhiên. 

Khi xếp hàng thì có người đứng trước, người đứng sau, giống như trong tập hợp số tự nhiên có số liền trước và số liền sau,…

Hoạt động 1 trang 13 Toán lớp 6 Tập 1: Trong hai điểm 5 và 8 trên tia số, điểm nào nằm trên trái, điểm nào nằm bên phải điểm kia?

Lời giải:

Dựa vào tia số ta nhận thấy: 

+) Do 5 < 8 điểm 5 nằm bên trái điểm 8;

+) Do 8 > 5 điểm 8 nằm bên phải điểm 5.

Hoạt động 2 trang 13 Toán lớp 6 Tập 1:

Điểm biểu diễn số tự nhiên nào nằm ngay bên trái điểm 8?

Điểm biểu diễn số tự nhiên nào nằm ngay bên phải điểm 8?

Lời giải:

Điểm biểu diễn số tự nhiên 7 (điểm 7) nằm ngay bên trái điểm 8.

Điểm biểu diễn số tự nhiên 9 (điểm 9) nằm ngay bên phải điểm 8.

Hoạt động 3 trang 13 Toán lớp 6 Tập 1: Cho n là một số tự nhiên nhỏ hơn 7. Theo em, điểm n nằm bên trái hay bên phải điểm 7?

Lời giải:

Vì n là một số tự nhiên nhỏ hơn 7 hay n < 7 nên điểm n nằm bên trái điểm 7.

Luyện tập trang 14 Toán lớp 6 Tập 1:

a) Hãy so sánh hai số tự nhiên sau đây, dùng kí hiệu “<” hay “>” để viết kết quả: m = 12 036 001 và n = 12 035 987.

b) Trên tia số (nằm ngang), trong hai điểm m và n, điểm nào nằm trước?

Lời giải:

a) Ta so sánh từng cặp chữ số ở cùng một hàng kể từ trái sang phải, nhận thấy ở hàng chục triệu, triệu, trăm nghìn, chục nghìn có các chữ số giống nhau, nhưng ở hàng nghìn ta thấy 6 > 5 nên 12 036 001 > 12 035 987 do đó m > n.

b) Vì m > n hay n < m nên trên tia số (nằm ngang) điểm n nằm trước điểm m.

Vận dụng trang 14 Toán lớp 6 Tập 1:

Theo dõi kết quả bán hàng trong ngày của một cửa hàng, người ta nhận thấy:

Số tiền thu được vào buổi sáng nhiều hơn vào buổi chiều;

Số tiền thu được vào buổi tối ít hơn vào buổi chiều.

Hãy so sánh số tiền thu được (đều là số tự nhiên) của cửa hàng đó vào buổi sáng và buổi tối.

Lời giải:

Gọi số tiền cửa hàng đó thu được vào buổi sáng, buổi chiều và buổi tối lần lượt là a, b, c (a, b, c là các số tự nhiên)

Số tiền thu được vào buổi sáng nhiều hơn vào buổi chiều nên a > b (1)

Số tiền thu được vào buổi tối ít hơn vào buổi chiều nên c < b hay b > c (2)

Theo tính chất bắc cầu: vì a > b (theo 1), b > c (theo 2) nên a > c. Do đó số tiền thu được vào buổi sáng nhiều hơn vào buổi tối.

Vậy số tiền thu được vào buổi sáng nhiều hơn vào buổi tối.

Câu hỏi trang 14 Toán lớp 6 Tập 1:

Trong các số: 3; 5; 8; 9, số nào thuộc tập hợp A = {x ∈ ℕ | x ≥ 5}, số nào thuộc tập hợp B = {x ∈ ℕ | x ≤ 5}?

Lời giải:

+) Vì A = {x ∈ ℕ | x ≥ 5} nên tập hợp A là những số tự nhiên lớn hơn hoặc bằng 5.

Do đó trong các số đã cho, các số thuộc tập hợp A là: 5; 8; 9.

+) Vì B = {x ∈ ℕ | x ≤ 5} nên tập hợp B là tập hợp những số tự nhiên nhỏ hơn hoặc bằng 5.

Do đó trong các số đã cho, các số thuộc tập hợp B là: 3; 5.

Bài tập

Bài 1.13 trang 14 Toán lớp 6 Tập 1: Viết thêm các số liền trước và liền sau của hai số 3 532 và 3 529 để được sáu số tự nhiên rồi sắp xếp sáu số tự nhiên đó theo thứ tự từ bé đến lớn.

Lời giải:

Số liền trước của số 3532 là: 3531

Số liền sau của số 3532 là: 3533

Số liền trước của số 3529 là: 3528

Số liền sau của số 3529 là: 3530

Ta thu được 6 số tự nhiên là:

3532; 3531; 3533; 3528; 3529; 3530

Vì 3528 < 3529 < 3530 < 3531 < 3532 < 3533

Sáu số trên được sắp xếp theo thứ tự từ bé đến lớn là:

3528; 3529; 3530; 3531; 3532; 3533.

Bài 1.14 trang 14 Toán lớp 6 Tập 1: Cho ba số tự nhiên a, b, c, trong đó a là số nhỏ nhất. Biết rằng trên tia số, điểm b nằm giữa hai điểm a và c. Hãy dùng kí hiệu "<" để mô tả thứ tự của ba số a, b, c. Cho ví dụ bằng số cụ thể.

Lời giải:

Vì số a nhỏ nhất nên điểm a nằm bên trái hai điểm b và c.

Mà điểm b nằm giữa hai điểm a và c nên điểm b nằm bên trái điểm c

Do đó b < c

Vì a bé nhất nên ta có a < b < c

* Ví dụ: a = 5; b = 7; c = 8 thỏa mãn a < b < c (do 5 < 7 < 8)

Số 5 bé nhất và điểm 7 nằm giữa hai điểm 5 và 8 trên tia số.

Bài 1.15 trang 14 Toán lớp 6 Tập 1: Liệt kê các phần tử của mỗi tập hợp sau:

a) M = {x ∈ ℕ | 10 ≤ x < 15}

b) K = {x ∈ ℕ* | x ≤ 3}

c) L = {x ∈ ℕ | x ≤ 3}

Lời giải:

a) M = {x ∈ ℕ | 10 ≤ x < 15}

Theo cách nêu dấu hiệu đặc trưng ở trên, ta thấy M là tập hợp các số tự nhiên lớn hơn hoặc bằng 10 và nhỏ hơn 15, đó là các số: 10; 11; 12; 13; 14.

Vậy bằng cách cách liệt kê các phần tử, ta có: M = {10; 11; 12; 13; 14}.

b) K = {x ∈ ℕ* | x ≤ 3}

Theo cách nêu dấu hiệu đặc trưng ở trên, ta thấy K là tập hợp các số tự nhiên x khác 0 (do x ∈ ℕ*) thỏa mãn x nhỏ hơn hoặc bằng 3, do đó x là các số: 1; 2; 3.

Vậy bằng cách cách liệt kê các phần tử, ta có: K = {1; 2; 3}.

c) L = {x ∈ ℕ | x ≤ 3}

Theo cách nêu dấu hiệu đặc trưng ở trên, ta thấy L là tập hợp các số tự nhiên nhỏ hơn hoặc bằng 3, đó là các số: 0; 1; 2; 3.

Do đó bằng cách cách liệt kê các phần tử, ta có: L = {0; 1; 2; 3}.

Bài 1.16 trang 14 Toán lớp 6 Tập 1: Ba bạn An, Bắc, Cường dựng cố định một cây sào thẳng đứng rồi đánh dấu chiều cao của các bạn lên đó bởi ba điểm. Cường đặt tên các điểm đó theo thứ tự từ dưới lên là A, B, C và giải thích rằng điểm A ứng với chiều cao của bạn An, B ứng với chiều cao bạn Bắc và C ứng với chiều cao của Cường. Biết rằng bạn An cao 150cm, bạn Bắc cao 153cm, bạn Cường cao 148cm. Theo em, Cường giải thích như thế có đúng không? Nếu không thì phải sửa như nào cho đúng?

Lời giải:

Vì cách đặt tên các điểm được đánh dấu tương tự như việc đặt tên các điểm trên tia số.

Chiều cao của các bạn theo thứ tự tăng dần là 148cm, 150cm, 153cm (do 148 < 150 < 153) ứng với chiều cao của Cường, An và Bắc

Do vậy cần đánh dấu các điểm theo thứ tự từ dưới lên là C, A, B.

Vì thế mà Cường đặt tên các điểm đó theo thứ tự từ dưới lên là A, B, C và giải thích rằng điểm A ứng với chiều cao của bạn An, B ứng với chiều cao bạn Bắc và C ứng với chiều cao của Cường là sai.

Phần 2: Lý thuyết bài học 

Với tóm tắt lý thuyết Toán lớp 6 Bài 3: Thứ tự trong tập hợp các số tự nhiên hay nhất, chi tiết sách Kết nối tri thức với cuộc sống sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 6.

A. Lý thuyết

+ Ta đã biết tập các số tự nhiên được kí hiệu là N, nghĩa là N = {0; 1; 2; 3;...}. Mỗi phần tử 0; 1; 2; 3; … được biểu diễn bởi một điểm trên tia số gốc 0 như hình vẽ:

+ Trong hai số tự nhiên khác nhau, luôn có một số nhỏ hơn số kia. Nếu số a nhỏ hơn số b thì trên tia số nằm ngang điểm a nằm bên trái điểm b. Khi đó, ta viết a < b hoặc b > a. Ta còn nói: điểm a nằm trước điểm b, hoặc điểm b nằm sau điểm a.

+ Mỗi số tự nhiên có đúng một số liền sau, chẳng hạn 9 là số liền sau của 8 (còn 8 là số liền trước của 9). Hai số 8 và 9 là hai số tự nhiên liên tiếp.

+ Nếu a < b và b < c thì a < c (tính chất bắc cầu). Chẳng hạn a < 5 và 5 < 7 suy ra a < 7.

Ví dụ 1. Viết thêm các số liền trước và số liền sau của hai số 2 567 và 3 012 để được sáu số tự nhiên và sắp xếp sáu số đó theo thứ tự giảm dần.

Lời giải

Số liền trước 2 567 là: 2 566;

Số liền sau 2 567 là: 2 568;

Số liền trước 3 012 là: 3 011;

Số liền sau 3 012 là 3 013;

Sắp xếp các số theo thứ tự giảm dần là: 3 013; 3 012; 3 011; 2 568; 2 567; 2 566.

+ Kí hiệu "≤ "  và "≥"

Ta còn dùng kí hiệu a ≤ b (đọc là “a nhỏ hơn hoặc bằng b”) để nói “a < b hoặc a = b”.

Ta còn dùng kí hiệu a ≥ b (đọc là “a lớn hơn hoặc bằng b”) để nói “a > b hoặc a = b”.

Tính chất bắc cầu còn có thể viết: nếu a ≤ b và b ≤ c thì a ≤ c .

Ví dụ 2. Cho tập hợp A = {x ∈ N* | x ≤ 14}. Hãy liệt kê các phần tử của tập hợp A.

Lời giải

Các số tự nhiên khác không nhỏ hơn hoặc bằng 14 là: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 12; 14.

A = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 12; 14} .

B. Bài tập

Bài 1. Điền các số thích hợp vào chỗ trống để được dãy các số tự nhiên liên tiếp:

a) …….; 102; ………;

b) 2 045; ………; ………;

c) ……; 17; …….; ………

Lời giải

a) Số liền trước của 102 là 101, số liền sau của 102 là 103. Nên ta có: 101; 102; 103.

b) Số liền sau của 2 045 là 2 046, số liền sau của 2 046 là 2 047. Nên ta có: 2 045; 2 046; 2 047.

c) Số liền trước của 17 là 16, số liền sau của 17 là 18, số liền sau của 18 là 19. Nên ta có: 16; 17; 18; 19.

Bài 2. Liệt kê các phần tử của mỗi tập hợp sau:

a) M = {x ∈ N | 10 ≤ x ≤ 15} 

b) N = {x ∈ N* | x ≤ 3}  ;

c) L = {x ∈ N | x ≤ 3} .

Lời giải

a) Các số tự nhiên lớn hơn hoặc bằng 10 nhỏ hơn 15 là: 10; 11; 12; 13; 14.

Theo cách liệt kê, ta viết: M = {10; 11; 12; 13; 14}.

b) Các số tự nhiên khác 0 và nhỏ hơn hoặc bằng 3 là: 1; 2; 3.

Theo cách liệt kê, ta viết: N = N = {1; 2; 3} .

c) Các số tự nhiên nhỏ hơn hoặc bằng 3 là: 0; 1; 2; 3.

Theo cách liệt kê, ta viết: L = {0; 1; 2; 3}..

Phần 3: Bài tập trắc nghiệm

Với 17 bài tập trắc nghiệm Toán lớp 6 Bài 3: Thứ tự trong tập hợp các số tự nhiên có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức với cuộc sống sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 6.

I. Nhận biết

Câu 1. Số liền trước và số liền sau của 180 là:

A. Số liền trước là 189 và số liền sau là 181.

B. Số liền trước là 179 và số liền sau là 181.

C. Số liền trước là 179 và số liền sau là 180.

D. Số liền trước là 170 và số liền sau là 181.

Câu 2. Trong hai số tự nhiên a và b, nếu a nhỏ hơn b thì trên tia số nằm ngang điểm a nằm ở đâu?

A. Bất kì trên tia số.

B. Bên phải điểm 0.

C. Bên phải điểm b.

D. Bên trái điểm b.

Câu 3. Nếu a < b và b < c thì:

A. a > c

B. a ≥ c

C. a < c

D.a ≤ c

Câu 4. Trục số biểu diễn điểm 3 là:

A.

B. 

C.

D. 

Câu 5. Điền số thích hợp vào chỗ chấm để được ba số tự nhiên liên tiếp: 10 024; …….; ……….

A. 1 025; 1 026.

B. 10 023; 1025.

C. 10 024; 10 025.

D. 10 025; 10 026.

Câu 6. Trong các dãy số sau đây, dãy nào sắp xếp theo thứ tự giảm dần:

A. 1 235; 456; 723; 985; 6 721.

B. 1 235; 6 721; 985; 723; 456.

C. 6 721; 1 235; 985; 723; 456.

D. 6 721; 985; 1 235; 723; 456.

Câu 7. Kí hiệu nghĩa là gì?

A. a nhỏ hơn b.

B. a bằng b.

C. a lớn hơn b.

D. a nhỏ hơn hoặc bằng b.

Câu 8. Cho trục số sau. Điểm D trên trục số biểu diễn cho số tự nhiên nào?

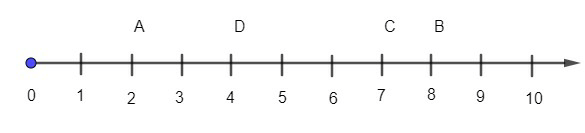
A. Số 2

B. Số 4

C. Số 7

D. Số 8

Câu 9. Cho hai số tự nhiên m = 12 036 và n= 12 134. Chọn đáp án đúng.

A. m < n;

B. m > n;

C. m ≥ n;

D. m ≤ n.

Câu 10. Cho số tự nhiên x, thỏa mãn 120 < x < 122.

A. x = 120;

B. x = 121;

C. x = 122;

D. Không tồn tại x.

II. Thông hiểu

Câu 1. Cho ba số tự nhiên a, b, c, trong đó a là số nhỏ nhất. Biết rằng trên tia số, điểm b nằm giữa hai điểm a và c. Hãy dùng kí kiệu “<” để mô tả thứ tự của ba số a, b và c. 

A. a < b < c;

B. a < c < b;

C. c < b < a;

D. c < b < a.

Câu 2. Sắp xếp các số sau theo thứ tự giảm dần: 1 029; 872; 2 304; 12 340; 756.

A. 2 304; 12 340; 1 029; 872; 756.

B. 2 304; 1 029; 12 340; 872; 756.

C. 12 340; 2 304; 1 029; 872; 756.

D. 12 340; 1 029; 2 304; 872; 756.

Câu 3. Liệt kê các phần tử của tập hợp sau: M = .

A. M = {10; 11; 12; 13; 14; 15}.

B. M = {10; 11; 12; 13; 14}.

C. M = {11; 12; 13; 14}.

D. M = {11; 12; 13; 14; 15}.

Câu 4. Trong các khẳng định sau, khẳng định nào đúng?

I)  1999 > 2003;

II) 100 000 là số tự nhiên lớn nhất;

III) 5 ≤ 5;

IV) Số 1 là số tự nhiên nhỏ nhất.

A. I đúng

B. II đúng

C. III đúng

D. IV đúng.

Câu 5. Cho tập hợp K = { x ∈ N* | x ≤ 3} . Chọn đáp án đúng.

A.3 ∉ K;

B.0 ∈ K ;

C.3 ∈ K ;

D.1 ∉ K.

III. Vận dụng

Câu 1. Ba bạn An, Bắc, Cường dựng cố định một cây sào thẳng đứng rồi đánh dấu chiều cao của các bạn lên đó bởi ba điểm. Điểm A ứng với chiều cao của bạn An, B ứng với chiều cao của Bắc và C ứng với chiều cao của Cường. Biết rằng bạn An cao 150 cm, bạn Bắc cao 153 cm, bạn Cường cao 148 cm. Sắp xếp các điểm A, B, C trên cây sào theo thứ tự từ thấp đến cao.

A. A, B, C.

B. A, C, B.

C. C, A, B.

D. C, B, A.

Câu 2. Theo dõi kết quả bán hàng trong ngày của một cửa hàng, người ta nhận thấy:

Số tiền thu được vào buổi sáng nhiều hơn vào buổi chiều;

Số tiền thu được vào buổi tối ít hơn vào buổi chiều.

Hãy so sánh số tiền thu được (đều là các số tự nhiên) của cửa hàng đó vào buổi sáng và buổi tối. 

A. Số tiền thu được buổi sáng ít hơn số tiền thu được vào buổi tối.

B. Số tiền thu được buổi sáng nhiều hơn số tiền thu được vào buổi tối.

C. Số tiền thu được buổi sáng bằng số tiền thu được vào buổi tối.

D. Không kết luận được.