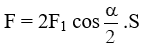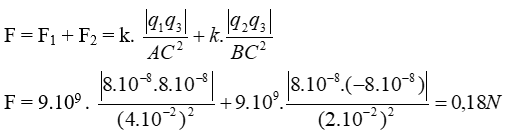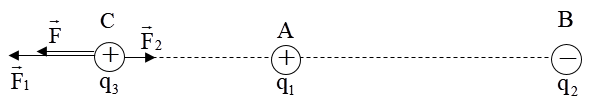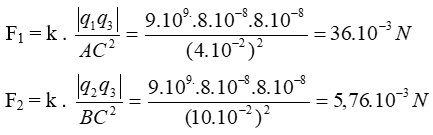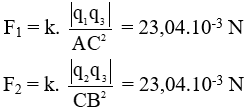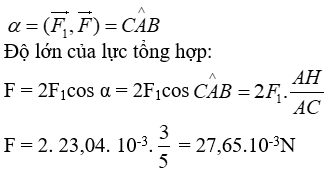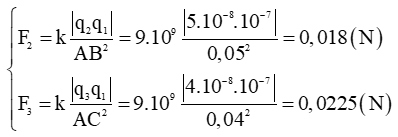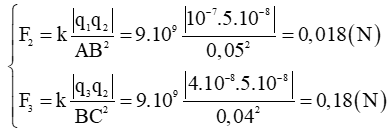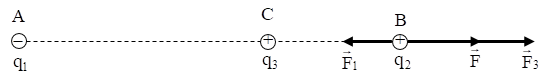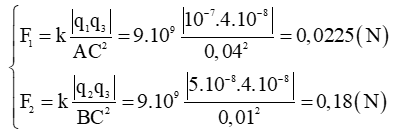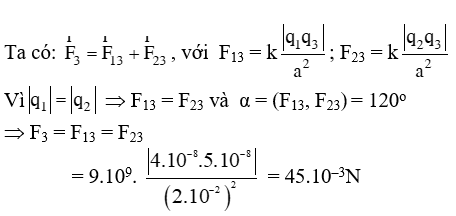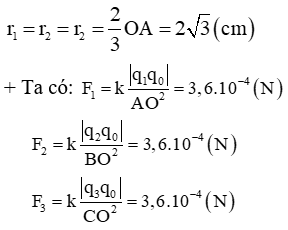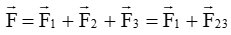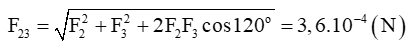Cách giải bài tập Lực điện tổng hợp tác dụng lên một điện tích hay, chi tiết

 Phương pháp & Ví dụ

- Khi một điện tích điểm q chịu tác dụng của nhiều lực tác dụng F→₁, F→₂, ... do các điện tích điểm q₁, q₂, ... gây ra thì hợp lực tác dụng lên q là: F→ = F→₁ + F→₂ + F→₃ + ... + F→_n

- Các bước tìm hợp lực F→ do các điện tích q₁; q₂; ... tác dụng lên điện tích q_o:

Bước 1: Xác định vị trí điểm đặt các điện tích (vẽ hình).

Bước 2: Tính độ lớn các lực F₁, F₂ lần lượt do q₁ và q₂ tác dụng lên q_o.

Bước 3: Vẽ hình các vectơ lực F→₁, F→₂

Bước 4: Từ hình vẽ xác định phương, chiều, độ lớn của hợp lực F→.

- Các trường hợp đặc biệt:

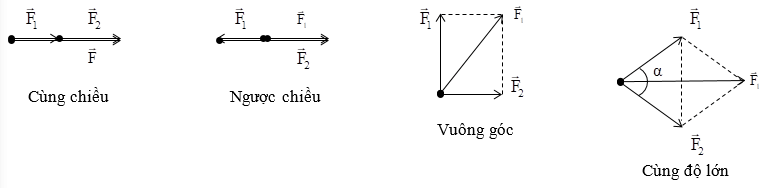
F→₁ và F→₂ cùng chiều thì: F = F₁ + F₂ (α = 0, cosα = 1).

F→₁ và F→₂ ngược chiều thì: F = |F₁ – F₂| (α = π, cosα = –1).

F→₁ và F→₂ vuông góc thì: 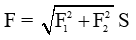(α = 90°, cosα = 0).

F→₁ và F→₂ cùng độ lớn (F₁ = F₂) thì: 

Tổng quát: F² = F₁² + F₂² + 2F₁F₂cosα(α là góc hợp bởi F→₁ và F→₂ ).

Ví dụ 1: Hai điện tích q₁ = 8.10^-8 C, q₂ = - 8.10^-8 C đặt tại A, B trong không khí (AB = 6 cm). Xác định lực tác dụng lên q₃ = 8.10^-8 C, nếu:

a) CA = 4cm, CB = 2cm

b) CA = 4cm, CB = 10cm

c) CA = CB = 5cm

Hướng dẫn:

Điện tích q₃ sẽ chịu hai lực tác dụng của q₁ và q₂ là F→₁ và F→₂.

Lực tổng hợp tác dụng lên q₃ là: F→ = F→₁ + F→₂

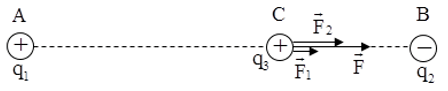
a) Trường hợp 1: CA = 4cm, CB = 2cm

Vì AC + CB = AB nên C nằm trong đoạn AB.

q₁, q₃ cùng dấu nên F→₁ là lực đẩy

q₂, q₃ trái dấu nên F→₂ là lực hút.

Trên hình vẽ, ta thấy F→₁ và F→₂ cùng chiều.

Vậy: F→ cùng chiều F→₁, F→₂ (hướng từ C đến B).

Độ lớn:

b) Trường hợp 2: CA = 4cm, CB = 10cm

Vì CB – CA = AB nên C nằm trên đường AB, ngoài khoảng AB, về phía A.

Ta có:

Theo hình vẽ, ta thấy F→₁ và F→₂ ngược chiều, F→₁ > F→₂.

Vậy:

    + F→ cùng chiều F→₁ (hướng xảy ra A, B)

    + Độ lớn F = F₁ – F₂ = 30,24.10^-3N

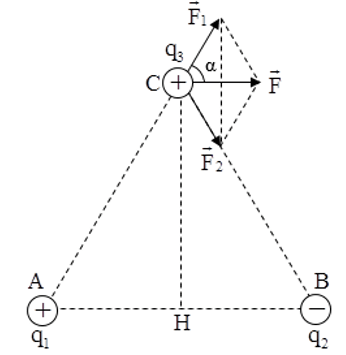
c) Trường hợp 3: Vì C cách đều A, B nên C nằm trên đường trung trực của đoạn AB.

Ta có:

Vì F₁ = F₂ nên F→ nằm trên phân giác góc (F→₁; F→₂).

⇒ F→ ⊥ CH(phân giác của hai góc kề bù) ⇒ F→ // AB

Nên:

Vậy: F→ có phương song song với AB, chiều hướng từ A đến B, độ lớn F = 27,65.10^-3N.

Ví dụ 2: Ba điện tích điểm q₁ = -10^-7 C, q₂ = 5.10^-8 C, q₃ = 4.10^-8 C lần lượt tại A, B, C trong không khí. Biết AB = 5 cm, BC = 1 cm, AC = 4 cm. Tính lực tác dụng lên mỗi điện tích.

Hướng dẫn:

Trong một tam giác tổng hai cạnh bất kì luôn lớn hơn cạnh còn lại nên dễ thấy A, B, C phải thẳng hàng.

Lực tác dụng lên điện tích q₁

    + Gọi lần lượt là lực do điện tích q₂ và q₃ tác dụng lên q₁

    + Ta có:

    + Lực F→₂, F→₃ được biểu diễn như hình

    + Gọi F→ là lực tổng hợp do q₂ và q₃ tác dụng lên q₁. Ta có: F→ = F→₂ + F→₃

    + Vì F→₂, F→₃ cùng phương cùng chiều nên ta có: F = F₂ + F₃ = 0,0405 N

Lực tác dụng lên điện tích q₂

    + Gọi F→₁, F→₃ lần lượt là lực do điện tích q₁ và q₃ tác dụng lên q₂

    + Ta có: 

    + Lực F→₁, F→₃ được biểu diễn như hình

    + Gọi F→ là lực tổng hợp do q₂ và q₃ tác dụng lên q₁. Ta có: F→ = F→₁ + F→₃

    + Vì F→₁, F→₃ cùng phương, ngược chiều nên ta có: F = F₃ – F₁ = 0,162 N

Lực tác dụng lên điện tích q₃

    + Gọi F→₁, F→₂ lần lượt là lực do điện tích q₁ và q₂ tác dụng lên q₃

    + Ta có: 

    + Lực F→₁, F→₂ được biểu diễn như hình

    + Gọi F→ là lực tổng hợp do q₁ và q₂ tác dụng lên q₃. Ta có: F→ = F→₁ + F→₂

    + Vì F→₁, F→₂ cùng phương cùng chiều nên ta có: F = F₁ + F₂ = 0,2025 N

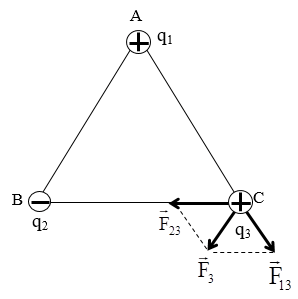
Ví dụ 3: Ba điện tích điểm q₁ = 4.10^-8C, q₂ = –4.10^-8C, q₃ = 5.10^-8C đặt trong không khí tại ba đỉnh ABC của một tam giác đều, cạnh a = 2cm. Xác định vectơ lực tác dụng lên q₃.

Hướng dẫn:

Vậy: Vectơ lực tác dụng lên q₃ có:

    + điểm đặt: tại C.

    + phương: song song với AB.

    + chiều: từ A đến B.

    + độ lớn: F₃ = 45.10^-3N.

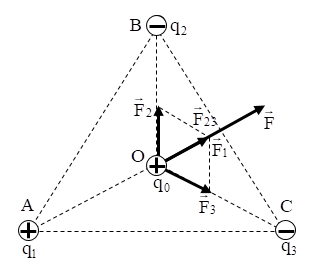
Ví dụ 4: Người ta đặt 3 điện tích q₁ = 8.10^-9 C, q₂ = q₃ = -8.10^-9 C tại 3 đỉnh của tam giác đều ABC cạnh a = 6 cm trong không khí. Xác định lực tác dụng lên q₀ = 6.10^-9 C đặt tại tâm O của tam giác.

Hướng dẫn:

Gọi F→₁, F→₂, F→₃ lần lượt là lực do điện tích q₁, q₂ và q₃ tác dụng lên q₀

    + Khoảng cách từ các điện tích đến tâm O:

    + Lực tác dụng F→₁, F→₂, F→₃ được biểu diễn như hình

    + Gọi F→ là lực tổng hợp tác dụng lên điện tích q₀:

Suy ra: 

    + Vì tam giác ABC đều nên F→₂₃ ↑ ↑ F→₁, nên: F = F₁ + F₂₃ = 7,2.10^-4 N

    + Vậy lực tổng hợp F→ có phương AO có chiều từ A đến O, độ lớn 7,2.10^-4

Ví dụ 5: Hai điện tích điểm q₁ = 3.10^-8 C, q₂ = 2.10^-8 C đặt tại hai điểm A và B trong chân không, AB = 5 cm. Điện tích q₀ = -2.10^-8 C đặt tại M, MA = 4 cm, MB = 3 cm. Xác định lực điện tổng hợp tác dụng lên q₀.

Hướng dẫn:

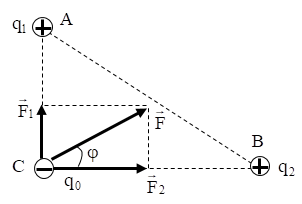
    + Nhận thấy AB² = AM² + MB² → tam giác AMB vuông tại M

    + Gọi F→₁, F→₂ lần lượt là lực do điện tích q₁ và q₂ tác dụng lên q₀

    + Ta có:

    + Vậy lực tổng hợp F→ tác dụng lên q₀ có điểm đặt tại C, phương tạo với F→₂ một góc φ ≈ 40° và độ lớn F = 5,234.10^-3 N.