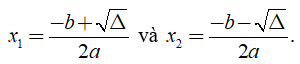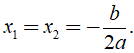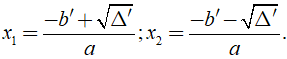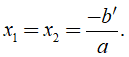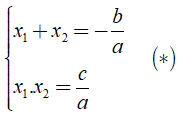Bài 9 : Tổng hợp lý thuyết Chương 4 Đại Số

1. Hàm số y = ax² (a ≠ 0)

Hàm số y = ax² (a ≠ 0) : Hàm số xác định với mọi số thực x

Tính chất biến thiên:

    + Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0.

    + Nếu a < 0 thì hàm đồng biến khi x < 0, nghịch biến khi x > 0.

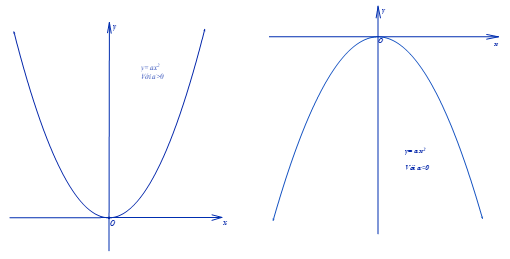
Đồ thị hàm số là một đường Parabol nhận gốc tọa độ O làm đỉnh, nhận trục tung làm trục đối xứng. Khi a > 0 thì Parabol có bề lõm quay lên trên, khi a < 0 thì Parabol có bề lõm quay xuống dưới.

2. Phương trình bậc hai một ẩn

Phương trình bậc hai một ẩn là phương trình có dạng: ax² + bx + c = 0. Trong đó x là ẩn số; a, b, c là những số cho trước gọi là các hệ số và a ≠ 0.

Đối với phương trình ax² + bx + c = 0 (a ≠ 0) và biệt thức Δ = b² - 4ac.

    + Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt

    + Nếu Δ = 0 thì phương trình có nghiệm kép là 

    + Nếu Δ < 0 thì phương trình vô nghiệm.

Đối với phương trình ax² + bx + c = 0 (a ≠ 0) và b = 2b'; Δ' = b'² - ac.

    + Nếu Δ' > 0, phương trình có hai nghiệm phân biệt

    + Nếu Δ' = 0, phương tình có nghiệm kép là 

    + Nếu Δ' < 0, phương trình đã cho vô nghiệm.

3. Định lý Vi – ét và ứng dụng

Định lý Viet: Nếu x₁, x₂ là hai nghiệm của phương trình

ax² + bx + c = 0, (a ≠ 0) thì

Chú ý: Trước khi sử dụng định lý Viet, chúng ta cần kiểm tra điều kiện phương trình có nghiệm, nghĩa là Δ ≥ 0.

Một số ứng dụng cơ bản của định lý Viet

    + Nhẩm nghiệm của một phương trình bậc hai:

Nếu a + b + c = 0 thì phương trình có hai nghiệm là x₁ = 1; x₂ = c/a.

Nếu a - b + c = 0 thì phương trình có hai nghiệm là x₁ = -1; x₂ = -c/a.

    + Tính giá trị của biểu thức g(x₁, x₂) trong đó g(x₁, x₂) là biểu thức đối xứng giữa hai nghiệm x₁, x₂ của phương trình (*):

        Bước 1: Kiểm tra điều kiện Δ ≥ 0, sau đó áp dụng định lý Viet.

        Bước 2: Biểu diễn biểu thức g(x₁, x₂) theo S = x₁ + x₂, P = x₁.x₂ từ đó tính được g(x₁, x₂).

Một số biểu thức đối xứng giữa hai nghiệm thường gặp:

    + Lập phương trình bậc hai có hai nghiệm là x₁, x₂ cho trước:

        ⋅ Bước 1: Tính S = x₁ + x₂; P = x₁.x₂.

        ⋅ Bước 2: Phương trình bậc hai nhận hai nghiệm x₁, x₂ là X² - S.X + P = 0.

4. Phương trình quy về phương trình bậc hai

a) Phương trình trùng phương

Phương trình trùng phương là phương trình có dạng ax⁴ + bx² + c = 0 (a ≠ 0)

Giải phương trình ax⁴ + bx² + c = 0 (a ≠ 0)

    + Đặt ẩn phụ x² = t, t ≥ 0

    + Giải phương trình ẩn phụ mới: at² + bt + c = 0

    + Với mỗi giá trị tìm được của t, lại giải phương trình x² = t.

b) Phương trình chứa ẩn ở mẫu

Khi giải phương trình chứa ẩn ở mẫu thức, ta làm như sau:

    + Bước 1: Tìm điều kiện xác định của phương trình

    + Bước 2: Quy đồng mẫu thức hai vế rồi khử mẫu thức

    + Bước 3: Giải phương trình vừa nhận được

    + Bước 4: Trong các giá trị tìm được của ẩn, loại các giá trị không thỏa mãn điều kiện xác định, các giá trị thỏa mãn điều kiện xác định là nghiệm của phương trình đã cho.

B. Bài tập tự luận

Câu 1: Biết đồ thị của hàm số 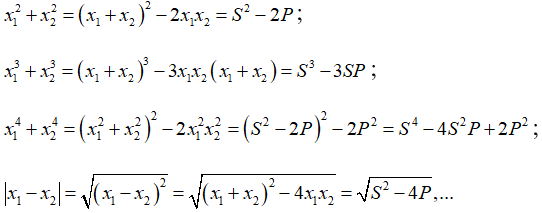, (a ≠ 0) đi qua điểm M (3; -6) . Hãy xác định giá trị của a

Câu 2: Cho hàm số y = 2x² có đồ thị là (P). Tìm trên (P) các điểm có tung độ bằng 4, vẽ đồ thị (P).

Câu 3: Tìm hàm số y = ax² biết đồ thị của nó đi qua điểm A(-1; 2) Với hàm số tìm được hãy tìm các điểm trên đồ thị có tung độ là 8.

Câu 4: Cho Parabol (P): y = x² và đường thẳng d: (2m - 1)x - m + 2 (m là tham số)

a) Chứng minh rằng với mọi m đường thẳng d luôn cắt (P) tại hai điểm phân biệt.

b) Tìm các giá trị của m để đường thẳng d luôn cắt (P) tại hai điểm phân biệt A(x₁; y₁), B(x₂; y₂) thỏa x₁y₁ + x₂y₂ .
Câu 5: Cho Parabol (P): y = x² và đường thẳng (d): y = 4x + 9 .

a) Vẽ đồ thị (P)

b) Viết phương trình đường thẳng (d₁) biết (d₁) song song với đường thẳng (d) và (d₁) tiếp xúc (P)

Câu 6: Cho parabol (P): y = x² và đường thẳng (d): y = -2ax - 4a (với a là tham số )

a) Tìm tọa độ giao điểm của (d) và (P) khi a = - 1/2 .

b) Tìm tất cả các giá trị của a để đường thẳng (d) cắt (P) taị hai điểm phân biệt có hoành độ x₁; x₂ thỏa mãn |x₁| + |x₂| = 3 .

Câu 7: Cho hai hàm số y = x² và y = mx + 4, với m là tham số.

a) Khi m = 3 , tìm tọa độ các giao điểm của hai đồ thị hàm số trên.

b) Chứng minh rằng với mọi giá trị m , đồ thị của hai hàm số đã cho luôn cắt nhau tại hai điểm phân biệt A₁(x₁; y₁) và A₂(x₂; y₂) Tìm tất cả các giá trị của m sao cho (y₁)² + (y₂)² = 7² .

Câu 8: Trong mặt phẳng tọa độ Oxy cho parabol (P) có phương trình 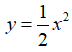 và hai điểm A, B thuộc (P) có hoành độ lần lượt là x_A = -1, x_B = 2

a) Tìm tọa độ của hai điểm A, B.

b) Viết phương trình đường thẳng (d) đi qua hai điểm A, B.

c) Tính khoảng cách từ điểm O (gốc tọa độ) tới đường thẳng (d) .

Câu 9: Cho parabol (P): y = 2x² và đường thẳng (d): y = x + 1.

a) Vẽ đồ thị của (P) và (d) trên cùng hệ trục tọa độ.

b) Bằng phép tính, xác định tọa độ giao điểm A và B của (P) và (d) Tính độ dài đoạn thẳng AB
Câu 10: Một người đi xe đạp từ A đến B cách nhau 24km. Khi đi từ B trở về A người đó tăng vận tốc thêm 4km/h so với lúc đi, nên thời gian về ít hơn thời gian đi là 30 phút. Tính vận tốc của xe đạp khi đi từ A đến B.

Câu 11: Quãng đường AB dài 120 km. Lúc 7h sang một xe máy đi từ A đến B. Đi được 3/4 quãng đường xe bị hỏng phải dừng lại 10 phút để sửa rồi đi tiếp với vận tốc kém vận tốc lúc đầu 10km/h. Biết xe máy đến B lúc 11h40 phút trưa cùng ngày. Giả sử vận tốc xe máy trên 3/4 quãng đường đầu không đổi và vận tốc xe máy trên 1/4 quãng đường sau cũng không đổi. Hỏi xe máy bị hỏng lúc mấy giờ?

Câu 12: Một công nhân theo kế hoạch phải làm 85 sản phẩm trong một khoảng thời gian dự định. Nhưng do yêu cầu đột xuất, người công nhân đó phải làm 96 sản phẩm. Do người công nhân mỗi giờ đã làm tăng thêm 3 sản phẩm nên người đó đã hoàn thành công việc sớm hơn so với thời gian dự định là 20 phút. Tính xem theo dự định mỗi giờ người đó phải làm bao nhiêu sản phẩm, biết rằng mỗi giờ chỉ làm được không quá 20 sản phẩm.