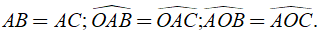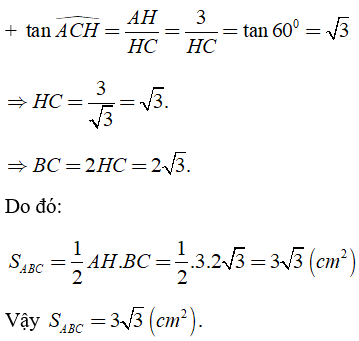Bài 6 : Tính chất của hai tiếp tuyến cắt nhau

1. Định lý về hai tiếp tuyến cắt nhau

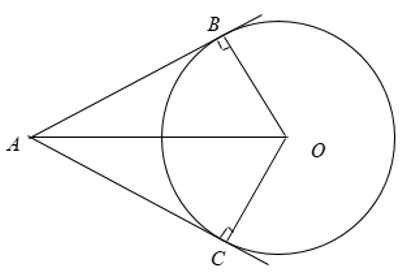
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

    + Điểm đó cách đều hai tiếp điểm.

    + Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

    + Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm

Ta có:

2. Đường tròn nội tiếp của tam giác.

Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác, còn tam giác gọi là ngoại tiếp đường tròn, khi đó tam giác đó gọi là tam giác ngoại tiếp đường tròn.

Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác

3. Đường tròn bàng tiếp tam giác.

Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia.

Tâm của đường tròn bàng tiếp trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, giao điểm này cùng nằm trên đường phân giác góc A.

Với một tam giác, có ba đường tròn bàng tiếp.

4. Ví dụ cụ thể

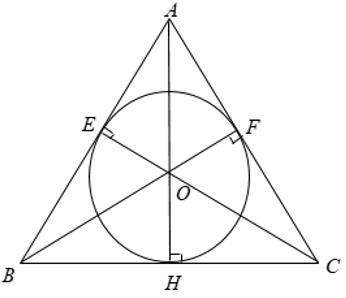
Câu 1: Cho tam giác đều ABC ngoại tiếp đường tròn bán kính bằng 1cm. Tính diện tích của tam giác ABC ?

Hướng dẫn:

Ta có: ΔABC đều nên đường cao đồng thời là đường trung trực, trung tuyến của tam giác

    + AH, CE, BF là ba đường trung trực giao nhau tại O.

⇒ O là tâm đường trong ngoại tiếp ΔABC.

Khi đó ta có: OH = OF = OE = R = 1cm

⇒ AH = BF = CE = 3R = 3cm

B. Bài tập tự luận

Câu 1: Cho nửa đường tròn tâm O đường kính AB. Vẽ các tia Ax vuông góc với AB, By vuông góc với AB ở cùng phía với nửa đường tròn. I là một điểm thuộc trên nửa đường tròn. Tiếp tuyến tại I cắt Ax, By tại C và D.

a) CMR: Tam giác COD là tam giác vuông

b) Tìm vị trí điểm I để chu vi tứ giác ACDB là nhỏ nhất. Tính chu vi theo R.

Câu 2: Cho tam giác ABC cân tại A nội tiếp đường tròn (O) . Các tiếp tuyến của (O) vẽ từ A và C cắt nhau tại M. Trên tia AM lấy điểm D sao cho AD = BC . Chứng minh: AC, BD, OM đồng quy