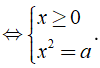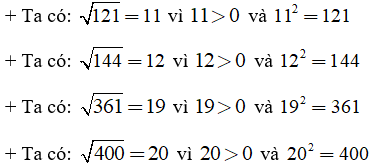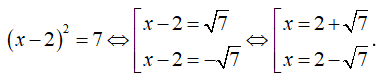Toán lớp 9 Bài 1: Căn bậc hai
Lý thuyết tổng hợp Toán học lớp 9 Bài 1: Căn bậc hai chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 9. Hy vọng bộ tổng hợp lý thuyết Toán lớp 9 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 9.
Bài 1 : Căn bậc hai
A. Lý thuyết
I. CĂN BẬC HAI
1. Khái niệm
Căn bậc hai của một số a không âm là số x sao cho x2 = a
2. Tính chất
- Số âm không có căn bậc hai
- Số 0 có đúng một căn bậc hai đó chính là số 0, ta viết √0 = 0
- Số dương a có đúng hai căn bậc hai là hai số đối nhau; số dương ký hiệu là √a, số âm ký hiệu là -√a
3. Ví dụ cụ thể
- Số 25 có hai căn bậc hai là 5 và -5.
- Số 7 có hai căn bậc hai là √7 và -√7
- Số -1 không có căn bậc hai.

II. CĂN BẬC HAI SỐ HỌC
1. Định nghĩa
- Với số dương a, số √a được gọi là căn bậc hai số học của a.
- Số 0 cũng được gọi là căn bậc hai số học của 0.
- Ta viết x = √a
- Ví dụ:
Căn bậc hai số học của 4 là √4 (= 2).
Căn bậc hai số học của 5 là √5 (≈ = 2,236067977...)
Ví dụ 1: Tìm căn bậc hai số học của các số sau đây: 121; 144; 361; 400
Giải:
2. Phép khai phương
- Phép khai phương là phép toán tìm căn bậc hai số học của số không âm (gọi tắt là khai phương).
- Khi biết một căn bậc hai số học của một số, ta dễ dàng xác định được các căn bậc hai của nó.
- Ví dụ:
Căn bậc hai số học của 49 là 7 nên 49 có hai căn bậc hai là 7 và -7.
Căn bậc hai số học cuả 100 là 10 nên 100 có hai căn bậc hai là 10 và -10
Căn bậc hai số học của 144 là 12 nên 144 có hai căn bậc hai là 12 và -12
3. Một số kết quả cần nhớ
- Với a ≥ 0 thì a = (√a)2.
- Với a ≥ 0, nếu x ≥ 0 và x2 = a thì x = √a.
- Với a ≥ 0 và x2 = a thì x = ±√a.
III. SO SÁNH CÁC CĂN BẬC HAI SỐ HỌC.
1. Định lý
Với hai số a và b không âm, ta có: a > b ⇔ √a > √b
2. Ví dụ cụ thể: So sánh
- 1 với √2.
Hướng dẫn:
Ta có 1 < 2 ⇒ √1 < √2 ⇒ 1 < √2.
- 3 với √7.
Hướng dẫn:
Ta có 9 > 7 ⇒ √9 > √7 ⇒ 3 > √7.
Ví dụ 1: So sánh:
a) 2 và √3 b) 7 và √51
Giải:
a) Ta có: 2 = √4 mà 4 > 3 nên √4 > √3 tức 2 > √3
b) Ta có: 7 = √49 mà 49 < 51 nên √49 < √51 tức 7 < √51
B. Bài tập tự luận
Câu 1: Tìm căn bậc hai của các số sau: 9; 9/25; 1,21; -144.
Lời giải
- Vì 9 > 0 nên 9 có hai căn bậc hai là 3 và -3, vì 32 = 9 và (-3)2 = 9.
- Vì 9/25 > 0 nên 9/25 có hai căn bậc hai là 3/5 và -3/5, vì (3/5)2 = 9/25 và (-3/5)2 = 9/25.
- Vì 1,21 > 0 nên 1,21 có hai căn bậc hai là 1,1 và -1,1, vì 1,12 = 1,21 và (-1,1)2 = 1,21.
- Theo tính chất, số âm không tồn tại căn bậc hai nên -144 không có căn bậc hai.
Câu 2: Giải các phương trình sau:
a) x2 = 5. b) x2 + 2 = 0 c) (x - 2)2 = 7
Lời giải
- Giải phương trình x2 = 5. Do 5 > 0 nên 5 có hai căn bậc hai là √5 và -√5
Suy ra 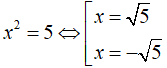
- Giải phương trình x2 = -2. Vì -2 < 0 nên -2 không có căn bậc hai. Suy ra phương trình vô nghiệm. Vậy S = ∅
- Giải phương trình (x - 2)2 = 7. Do 7 > 0 nên 7 có hai căn bậc hai là √7 và -√7.
Suy ra
Vậy S = {2 - √7; 2 + √7}
Trình bày gọn:
Câu 3: So sánh các số sau:
a) 6 và √35 b) 3 và √5 c) √7 với √5.
Lời giải
a) Ta có: 36 > 35 ⇒ √36 > √35 ⇒ 6 > √35
b) Ta có: 9 > 5 ⇒ √9 > √5 ⇒ 3 > √5
c) Ta có: 7 > 5 ⇒ √7 > √5
Câu 4: Chọn đáp án đúng trong các phương án sau?
A. √2 > √3. B. √5 < 2. C. √7 < 3 D. √-4 = 2.
Hiển thị lời giải- Ta có 2 < 3 ⇒ √2 < √3. Đáp án A sai.
- Ta có 5 > 4 ⇒ √5 > √4 ⇒ √5 > 2. Đáp án B sai.
- Ta có 7 < 9 ⇒ √7 < √9 ⇒ √7 < 3. Đáp án C đúng.
- Theo định nghĩa không tồn tại căn bậc hai của số âm. Đáp án D sai.
Chọn đáp án C.
Câu 5: Trong các nhận xét sau, nhận xét nào sai ?
A. Căn bậc hai số học của 36 là 6 và -6.
B. 25 có hai căn bậc hai là 5 và -5.
C. Số 0 có đúng một căn bậc hai là chính nó.
D. Số -7 không có căn bậc hai.
Hiển thị lời giải- Căn bậc hai số học của 36 là 6. Đáp án A sai.
Chọn đáp án A.
Câu 6: Căn bậc hai số học của -81 là ?
A. 9 B. -9 C. ±9 D. Không xác định
Hiển thị lời giảiKhông tồn tại căn bậc hai số học của số âm
Chọn đáp án D.
Câu 7: Một mảnh vườn hình vuông có diện tích bằng diện tích của một hình chữ nhật có chiều dài là 9 m và chiều rộng là 4 m. Hỏi cạnh của mảnh vườn hình vuông đó bằng bao nhiêu ?
A. 6m B. 8m C. 7m D. 36m
Hiển thị lời giảiDiện tích của hình chữ nhật là 9.4 = 36 (m2)
Diện tích của mảnh đất hình vuông là 36 (m2) nên cạnh hình vuông là √36 = 6 (m) (vì độ dài cạnh luôn dương)
Chọn đáp án A.