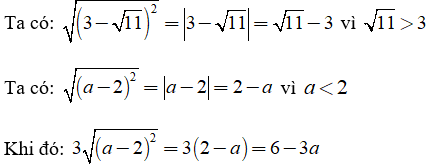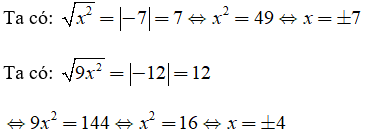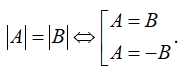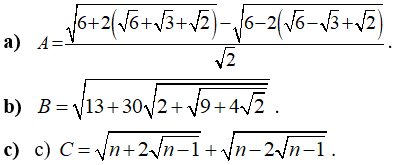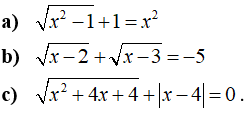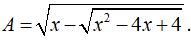Toán lớp 9 Bài 2 : Căn thức bậc hai và hằng đẳng thức
Lý thuyết tổng hợp Toán lớp 9 Bài 2 : Căn thức bậc hai và hằng đẳng thức chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 9. Hy vọng bộ tổng hợp lý thuyết Toán lớp 9 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 9.
Bài 2 : Căn thức bậc hai và hằng đẳng thức
A. Lý thuyết
I. CĂN THỨC BẬC HAI
1. Định nghĩa
Với A là một biểu thức đại số, người ta gọi √A là căn thức bậc hai của A, còn A là biểu thức lấy căn hay còn gọi là biểu thức dưới dấu căn.
2. Điều kiện có nghĩa(hay có nghĩa) của một căn thức bậc hai
√A xác định(có nghĩa) ⇔ A ≥ 0
3. Ví dụ cụ thể
- 
xác định ⇔ 3x ≥ 0 ⇔ x ≥ 0.
- 
xác định ⇔ 3 - 7x ≥ 0 ⇔ x ≤ 3/7.
- 
xác định ⇔ 2 - 3x ≥ 0 ⇔ x ≤ 2/3.
- 
xác định ⇔ x - 6 ≥ 0 ⇔ x ≥ 6.
- 
xác định.
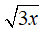
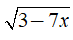
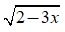
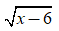
II. HẰNG ĐẲNG THỨC
Muốn khai căn một biểu thức, ta dùng hằng đẳng thức √(A2) = |A|.
Ví dụ 1: Rút gọn biểu thức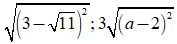 
với a < 2
Giải:
Ví dụ 2: Tìm x biết 
Giải:
III. MỘT SỐ KIẾN THỨC CẦN NHỚ
1. Giá trị tuyệt đối
• Định nghĩa 
• Hệ quả
|A| ≥ 0, ∀ A
|A| = |-A|
|A| = A ⇔ A ≥ 0; |A| = -A ⇔ A ≤ 0; |A| = 0 ⇔ A = 0
2. Dấu của một tích, một thương
B. PHƯƠNG PHÁP GIẢI TOÁN
DẠNG 1: Tìm điều kiện để một để một căn thức bậc hai xác định.
• √A xác định (hay có nghĩa) ⇔ A ≥ 0
• Giải bất phương trình A ≥ 0
• Kết luận.
DẠNG 2: Khai căn một biểu thức – Tính giá trị một biểu thức chứa căn
• Khai căn nhờ hằng đẳng thức √(A2) = |A|
• Rút gọn
DẠNG 3: Phân tích thành nhân tử
• Viết A ≥ 0 thành (√A)2
• Sử dụng A2 - B2 = (A - B)(A + B)
• Sử dụng A2 ± 2AB + B2 = (A ± B)2
• Thêm, bớt tạo thành hằng đẳng thức
DẠNG 4: Giải phương trình
• Khai căn một biểu thức
• Giải phương trình chứa dấu giá trị tuyệt đối
B. Bài tập tự luận
Câu 1: Rút gọn các biểu thức sau:
Câu 2: Giải các phương trình sau
Câu 3: Cho biểu thức:
a) Tìm tập xác định của biểu thức.
b) Rút gọn biểu thức A.
