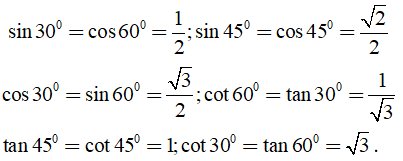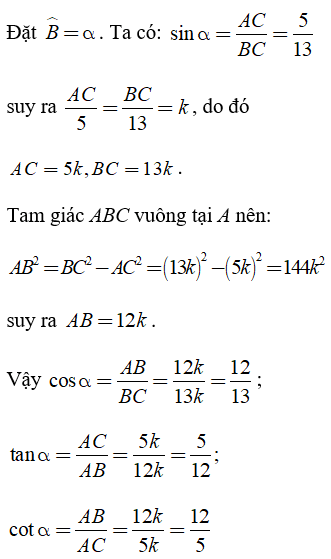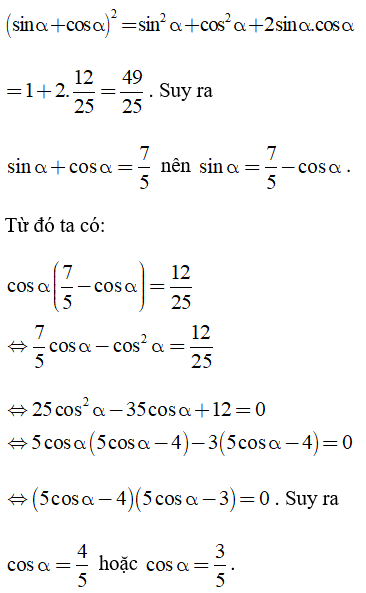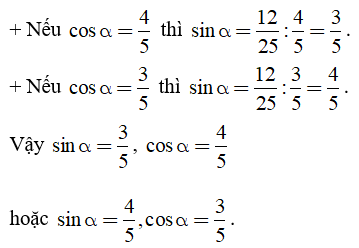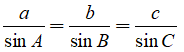Toán lớp 9 Bài 2 : Tỉ số lượng giác của góc nhọn
Lý thuyết tổng hợp Toán lớp 9 Bài 2 : Tỉ số lượng giác của góc nhọn chọn lọc năm 2021 – 2022 mới nhất gồm tóm tắt lý thuyết và hơn 500 bài tập ôn luyện Toán 9. Hy vọng bộ tổng hợp lý thuyết Toán lớp 9 sẽ giúp học sinh củng cố kiến thức, ôn tập và đạt điểm cao trong các bài thi trắc nghiệm môn Toán học 9.
Bài 2 : Tỉ số lượng giác của góc nhọn
1. Định nghĩa
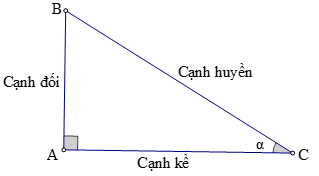
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sinα.
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu là cosα.
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu là tanα.
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu là cotα.
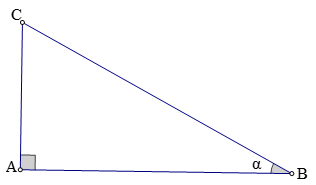
Hay sinα = AB/BC; cosα = AC/BC; tanα = AB/AC; cotα = AC/AB.
Nhận xét: Nếu α là một góc nhọn thì 0 < sinα < 1; 0 < cosα < 1; tanα > 0; cotα > 0
2. Tỉ số lượng giác của hai góc phụ nhau
Với hai góc α, β mà α + β = 90°,
Ta có: sinα = cosβ; cosα = sinβ; tanα = cotβ; cotα = tanβ.
Nếu hai góc nhọn α và β có sinα = sinβ hoặc cosα = cosβ thì α = β.
3. Một số góc đặc biệt
Với một số góc đặc biệt ta có:
4. Ví dụ cụ thể
Câu 1: Biết sinα = 5/13. Tính cosα, tanα và cotα.
Hướng dẫn:
Xét ΔABC vuông tại A.
Câu 2: Biết sinα.cosα = 12/25. Tính sinα, cosα.
Hướng dẫn:
Biết sinα.cosα = 12/25. Để tính sinα,cosα ta cần tính sinα + cosα rồi giải phương trình với ẩn là sinα hoặc cosα.
Ta có:
B. Bài tập tự luận
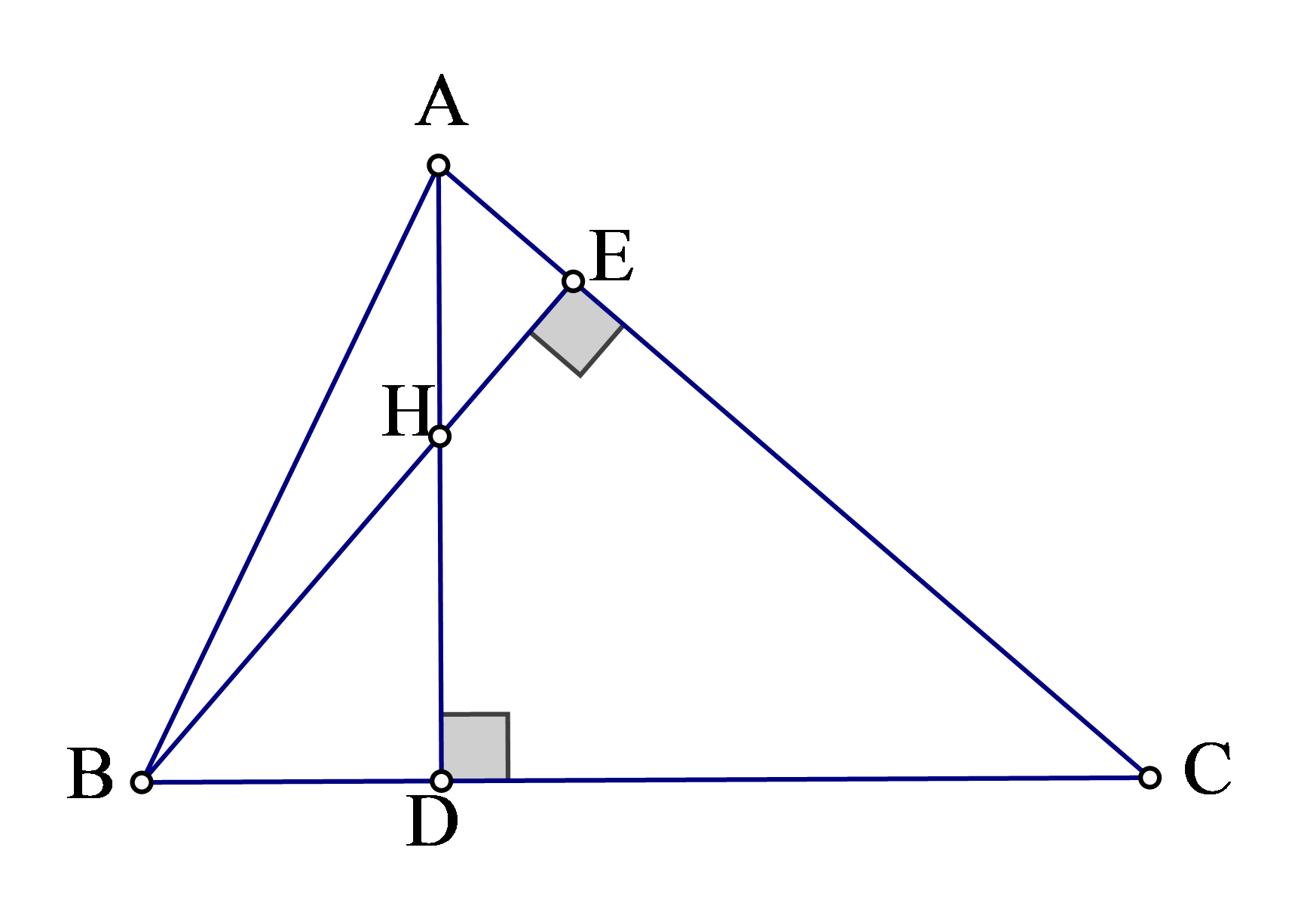
Câu 1: Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD:HA = 1:2 . Chứng minh rằng tgB.tgC = 3 .
Câu 2: Cho tam giác ABC nhọn. Gọi a, b, c lần lượt là độ dài các cạnh đối diện với các đỉnh A, B, C. Chứng minh rằng: 
Bài viết liên quan
- Toán lớp 9 Bài 6 : Tổng hợp lý thuyết Chương 2 Đại Số
- Toán lớp 9 Bài 1 : Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Toán lớp 9 Bài 3 : Một số hệ thức về cạnh và góc trong tam giác vuông
- Toán lớp 9 Bài 4 : Ứng dụng thực tế các tỉ số lượng giác của góc nhọn
- Toán lớp 9 Bài 5 : Tổng hợp lý thuyết Chương 1 Hình học
