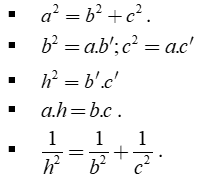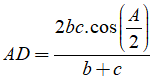Bài 5 : Tổng hợp lý thuyết Chương 1 Hình học

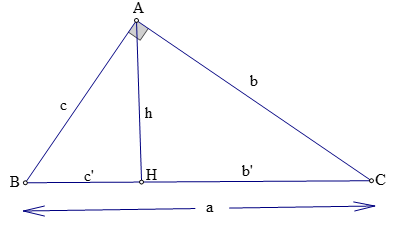
1. Hệ thức về cạnh và đường cao

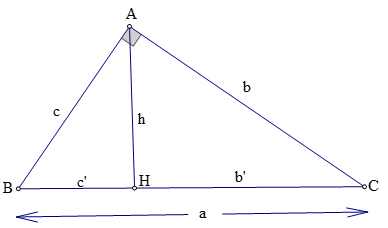
Tam giác ABC vuông tại A, đường cao AH, ta có:

Chú ý: Diện tích tam giác vuông: S = (1/2)bc = (1/2)ah.

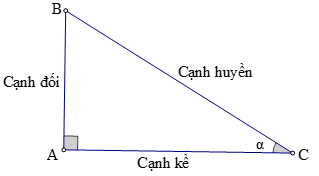
2. Tỉ số lượng giác của góc nhọn.

    + Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sinα.

    + Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu là cosα.

    + Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu là tanα.

    + Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu là cotα.

Hay sinα = AB/BC; cosα = AC/BC; tanα = AB/AC; cotα = AC/AB.

Tính chất:

    + Nếu α là một góc nhọn thì 0 < sinα < 1; 0 < cosα < 1; tanα > 0; cotα > 0.

    Ta có: sin²α + cos²α = 1;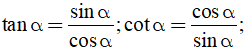 tanα.cotα = 1

    + Với hai góc nhọn α, β mà α + β = 90°.

    Ta có: sinα = cosβ; cosα = sinβ; tanα = cotβ; cotα = tanβ.

    Nếu hai góc nhọn α và β có sinα = sinβ hoặc cosα = cosβ thì α = β.

3. Hệ thức về cạnh và góc trong tam giác vuông.

Trong một tam giác vuông, mỗi cạnh góc vuông bằng:

    + Cạnh huyền nhân với sin góc đối hay nhân với côsin góc kề.

    + Cạnh góc vuông kia nhân với tan của góc đối hay nhân với cotg của góc kề.

    b = a.sinB = a.cosC; c = a.sinC = a.cosB; b = c.tgB = c.cotgC; c = b.tgC = b.cotgC.

Chú ý: Trong một tam giác vuông nếu cho trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông) thì ta sẽ tìm được các yếu tố còn lại.

B. Bài tập tự luận

Câu 1: Cho tam giác cân ABC có đáy BC = 2a , cạnh bên bằng b (b > a) .

a) Tính diện tích tam giác ABC

b) Dựng BKk ⊥ AC . Tính tỷ số  .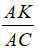

Câu 2: Cho tam giác ABC với các đỉnh A, B, C và các cạnh đối diện với các đỉnh tương ứng là: a, b, c .

a) Tính diện tích tam giác ABC theo a, b , c

b) Chứng minh: a² + b² + c² ≥ 4√3S

Câu 3: Biết sinα 5/13 . Tính cosα, tanα và cotα .

Câu 4: Biết sinα.cosα = 12/25. Tính sinα.cosα.

Câu 5: Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD:HA = 1:2 . Chứng minh rằng tgB.tgC = 3 .

Câu 6: Cho tam giác ABC nhọn. Gọi a, b, c lần lượt là độ dài các cạnh đối diện với các đỉnh A, B, C. Chứng minh rằng: 

Câu 7: Ở một cái thang đơn dài có ghi “để dảm bảo an toàn cần đặt thang sao cho tạo với mặt đất một góc α thì phải thỏa mãn 60° < α < 75° . Vậy phải đặt thang cách vật thang dựa khoảng bao nhiêu để đảm bảo an toàn?

Câu 8: Cho tam giác ABC vuông tại B có BC = 20m, 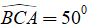. Một đường thẳng song song với BC cắt AB, AC lần lượt tại D, E. Biết BD = 5m . Tính độ dài AE là?

Câu 9: Tính diện tích tam giác ABC biết 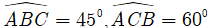 bán kính đường tròn ngoại tiếp tam giác ABC là R .

Câu 10: Cho tam giác ABC với các đỉnh A, B, C và các cạnh đối diện với các đỉnh tương ứng là: a, b, c . Chứng minh rằng:

a) a² = b² + c² - 2bccosA

b) Gọi D là chân đường phân giác trong góc A . Chứng minh: 

Câu 11: Không dùng máy tính và bảng số hãy chứng minh rằng  .