Trắc nghiệm Toán 10 Bài 7: Các khái niệm mở đầu

Bộ 15 bài tập trắc nghiệm Toán 10 Bài 7: Các khái niệm mở đầu có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 7.

385

Tải tài liệu

« Trang trước

Trang sau »

Trắc nghiệm Toán 10 Bài 7: Các khái niệm mở đầu - Kết nối tri thức

Câu 1. Mệnh đề nào sau đây là đúng?

A. Có duy nhất một vectơ cùng phương với mọi vec tơ;

B. Có vô số vectơ cùng phương với mọi vectơ;

C. Không có vectơ nào cùng phương với mọi vectơ;

D. Có ít nhất hai vectơ cùng phương với mọi vectơ.

Hiển thị đáp án

Đáp án: B

Giải thích:

Vectơ - không cùng hướng với mọi vectơ nên cùng phương với mọi vectơ.

Mà có vô số vec tơ – không. Do đó B đúng.

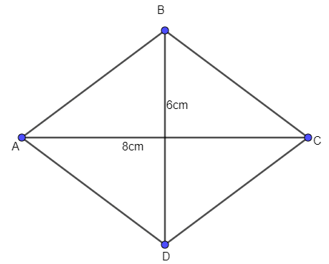
Câu 2. Cho hình thoi ABCD có độ dài hai đường chéo AC, BD lần lượt là 8 cm và 6 cm. Tính độ dài vectơ $\vec{A B}$ .

15 Bài tập Các khái niệm mở đầu (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

A. 10 cm;

B. 3 cm;

C. 4 cm;

D. 5cm.

Hiển thị đáp án

Đáp án: D

Giải thích:

15 Bài tập Các khái niệm mở đầu (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Gọi O là giao điểm của hai đường chéo AC và BD. Khi đó O là trung điểm của AC, cũng là trung điểm của BD.

⇒ AO = OC = $\frac{A C}{2} = \frac{8}{2} = 4 c m .$

⇒ BO = OD = $\frac{B D}{2} = \frac{6}{2} = 3 c m .$

Xét tam giác AOB vuông tại O, có:

AB² = AO² + BO² (định lí Py – ta – go)

⇔ AB² = 4² + 3² = 16 + 9 = 25

⇔ AB = 5 (cm)

$\Rightarrow |\vec{A B}| = A B = 5 c m .$

Vậy độ dài $\vec{A B}$ là 5cm.

Câu 3. Cho hình bình hành ABCD. Vectơ nào dưới đây bằng $\vec{C D}$ .

A. $\vec{D C}$ ;

B. $\vec{A D}$ ;

C. $\vec{C B}$ ;

D. $\vec{B A}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Vì ABCD là hình bình hành nên AB // CD nên $\vec{B A}$ và $\vec{C D}$ cùng phương. Do đó $\vec{B A}$ và $\vec{C D}$ cùng hướng.

Mặt khác AB = CD (tính chất hình bình hành)

Suy ra $\vec{B A} = \vec{C D}$ .

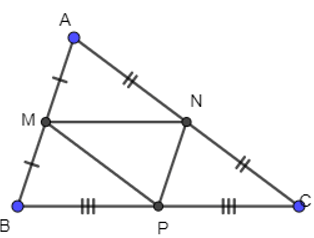
Câu 4. Cho tam giác ABC có M là trung điểm của AB, N là trung điểm của AC và P là trung điểm của BC.

15 Bài tập Các khái niệm mở đầu (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Phát biểu nào dưới đây là sai.

A. $\vec{M N} = \vec{P C}$ ;

B. $\vec{A A}$ cùng hướng với $\vec{P P}$ ;

C. $\vec{M B} = \vec{A M}$ ;

D. $\vec{M N} = \vec{P B}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

+) Xét tam giác ABC, có:

M là trung điểm AB

N là trung điểm của AC

⇒ MN là đường trung bình của tam giác ABC

⇒ MN // BC và MN = $\frac{1}{2}$ BC

Mà BP = PC = $\frac{1}{2}$ BC (P là trung điểm của BC)

⇒ MN = CP = PB (1)

Vì MN // BC nên MN // CP. Khi đó $\vec{M N}$ và $\vec{P C}$ cùng phương. Suy ra $\vec{M N}$ và $\vec{P C}$ cùng hướng (2)

Từ (1) và (2) suy ra $\vec{M N}$ = $\vec{C P}$ . Do đó đáp án A đúng.

Tương tự MN //BC hay MN // PB. Khi đó $\vec{M N}$ và $\vec{P B}$ cùng phương nhưng ngược hướng (3)

Từ (1) và (3) suy ra $\vec{M N}$ không bằng $\vec{P B}$ . Do đó đáp án D sai.

+) Ta có $\vec{A A}$ và $\vec{P P}$ là các vectơ – không.

Mà mọi vectơ – không có cùng độ dài và cùng hướng nên bằng nhau

Suy ra $\vec{A A}$ cùng hướng với $\vec{P P}$ . Do đó đáp án B đúng.

+) Hai vec tơ $\vec{A M}$ và $\vec{M B}$ cùng hướng

Vì M là trung điểm của AB nên AM = MB

Suy ra $\vec{A M} = \vec{M B}$ . Do đó đáp án C đúng.

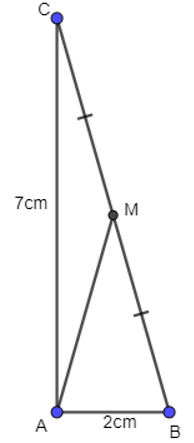
Câu 5. Cho tam giác ABC vuông tại A, có AB = 2cm, AC = 7cm. Điểm M là trung điểm của BC. Tính độ dài vectơ AM.

A. $|\vec{A M}| = \sqrt{53}$ cm

B. $|\vec{A M}| = 3$ cm

C. $|\vec{A M}| = \frac{\sqrt{53}}{2}$ cm

D. $|\vec{A M}| = \frac{3}{2}$ cm

Hiển thị đáp án

Đáp án: C

Giải thích:

15 Bài tập Các khái niệm mở đầu (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Xét tam giác ABC vuông tại A, có:

BC² = AB² + AC² (định lí Py – ta – go)

⇔ BC² = 2² + 7² = 4 + 49 = 53

⇔ BC = $\sqrt{53}$ cm

Ta lại có M là trung điểm BC

⇒ AM = $\frac{1}{2}$ BC (tính chất đường trung tuyến)

⇒ AM = $\frac{\sqrt{53}}{2}$ cm.

⇒ $|\vec{A B}| = A B = \frac{\sqrt{53}}{2} c m$

Vậy độ dài vectơ $\vec{A B}$ là $\frac{\sqrt{53}}{2} c m .$

Câu 6. Vectơ có điểm đầu là P điểm cuối là Q được kí hiệu là:

A. $\vec{P Q}$ ;

B. $\vec{Q P}$ ;

C. PQ;

D. $\bar{P Q}$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

Vectơ có điểm đầu là P và điểm cuối là Q được kí hiệu là

\bar{P Q}

Câu 7. Hai vectơ được gọi là bằng nhau khi và chỉ khi:

A. hai vectơ độ dài bằng nhau;

B. hai vectơ trùng nhau;

C. hai vectơ cùng phương và độ dài bằng nhau;

D. hai vectơ cùng hướng và độ dài bằng nhau.

Hiển thị đáp án

Đáp án: A

Giải thích:

Hai vectơ được gọi là bằng nhau khi và chỉ khi hai vectơ cùng hướng và độ dài bằng nhau.

Câu 8. Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Đẳng thức nào sau đây sai?

A. $\vec{A B} = \vec{D C}$ ;

B. $\vec{O B} = \vec{D O}$ ;

C. $\vec{O A} = \vec{O C}$ ;

D. $\vec{C B} = \vec{D A}$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Vì ABCD là hình bình hành nên AB // CD và AB = CD hay hai vectơ $\vec{A B}$ và $\vec{D C}$ cùng hướng và cùng độ dài

Suy ra $\vec{A B} = \vec{D C}$ . Do đó A đúng.

Hai vectơ $\vec{O B}$ và $\vec{D O}$ có giá trùng nhau nên cùng hướng và OB = DO (O là trung điểm của BD).

Suy ra $\vec{O B} = \vec{D O}$ . Do đó đáp án B đúng.

Hai vectơ $\vec{O A}$ và $\vec{O C}$ có giá trùng nhau nhưng ngược hướng và OA = OC (O là trung điểm của AC).

Suy ra $\vec{O A}$ không bằng $\vec{O C}$ . Do đó đáp án C sai.

Vì ABCD là hình bình hành nên AD // CB và CB = DA hay hai vectơ $\vec{C B}$ và $\vec{D A}$ cùng hướng và cùng độ dài

Suy ra $\vec{D A} = \vec{C B}$ . Do đó D đúng.

Câu 9. Cho hình vuông MNPQ có chu vi bằng 12. Độ dài vectơ $\vec{M P}$ là:

A. 3;

B. $3 \sqrt{2}$ ;

C. 6;

D. $6 \sqrt{2}$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Độ dài cạnh của hình vuông là: 12:4 = 3.

Khi đó MN = NP = PQ = MQ = 3

Xét tam giác MQP vuông tại Q, có:

MP² = MQ² + QP² (định lí Py – ta – go)

⇔ MP² = 3² + 3² = 9 + 9 = 18

⇔ MP = $3 \sqrt{2}$

⇒ $|\vec{M P}| = M P = 3 \sqrt{2} .$

Vậy độ dài vectơ $\vec{M P}$ là $3 \sqrt{2}$ .

Câu 10. Cho tam giác ABC có bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh A, B, C?

A. 3;

B. 4;

C. 5;

D. 6.

Hiển thị đáp án

Đáp án: D

Giải thích:

Các vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh A, B, C là: $\vec{A B}, \vec{A C}, \vec{B C}, \vec{B A}, \vec{C A}, \vec{C B} .$

Vậy tổng có 6 vectơ.

Câu 11. Điền từ thích hợp vào dấu (…) để được mệnh đề đúng. “Hai vectơ ngược hướng thì …”:

A. có giá song song;

B. cùng phương;

C. có độ dài bằng nhau;

D. có giá trùng nhau.

Hiển thị đáp án

Đáp án: B

Giải thích:

Hai vectơ ngược hướng thì cùng phương.

Câu 12. Cho hình vẽ sau:

15 Bài tập Các khái niệm mở đầu (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Cặp vectơ nào cùng hướng?

A. $\vec{a}$ và $\vec{b}$ ;

B. $\vec{a}$ và $\vec{c}$ ;

C. $\vec{c}$ và $\vec{b}$ ;

D. $\vec{c}$ và $\vec{e}$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

Hai vectơ $\vec{a}$ và $\vec{b}$ cùng nằm trên một đường thẳng hay chúng có giá trùng nhau nên $\vec{a}$ và $\vec{b}$ là hai vectơ cùng phương. Do đó hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng.

Hai vectơ $\vec{a}$ và $\vec{c}$ nằm trên hai đường thẳng song song hay chúng có giá song song nhau nên $\vec{a}$ và $\vec{c}$ là hai vectơ cùng phương. Do đó hai vectơ $\vec{a}$ và $\vec{c}$ ngược hướng.

Hai vectơ $\vec{b}$ và $\vec{c}$ nằm trên hai đường thẳng song song hay chúng có giá song song nhau nên $\vec{b}$ và $\vec{c}$ là hai vectơ cùng phương. Do đó hai vectơ $\vec{b}$ và $\vec{c}$ ngược hướng.

Hai vectơ $\vec{e}$ và $\vec{c}$ không cùng phương.

Vậy các cặp vec tơ cùng hướng là $\vec{a}$ và $\vec{b}$ .

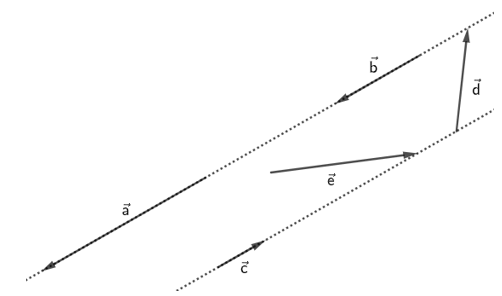
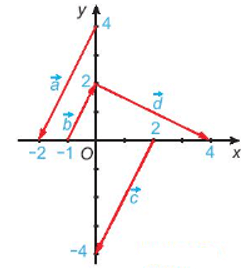
Câu 13. Cho hình vẽ:

15 Bài tập Các khái niệm mở đầu (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Có bao nhiêu cặp vectơ không cùng phương trên hình vẽ?

A. 3;

B. 2;

C. 1;

D. 0.

Hiển thị đáp án

Đáp án: A

Giải thích:

Quan sát hình vẽ ta thấy:

Các cặp vectơ không cùng phương là: $\vec{a}$ và $\vec{d}$ , $\vec{b}$ và $\vec{d}$ , $\vec{c}$ và $\vec{d}$ .

Vậy có tất cả 3 cặp vectơ không cùng phương.

Câu 14. Cho hình thang cân ABCD

15 Bài tập Các khái niệm mở đầu (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Nhận xét nào sau đây đúng về cặp vec tơ $\vec{A C}$ và $\vec{B D}$ ?

A. $\vec{A B} = \vec{B D}$ ;

B. Hai vectơ $\vec{A C}$ và $\vec{B D}$ cùng phương;

C. Hai vectơ $\vec{A C}$ và $\vec{B D}$ cùng hướng;

D. Hai vectơ $\vec{A C}$ và $\vec{B D}$ cùng độ dài.

Hiển thị đáp án

Đáp án: D

Giải thích:

Vì AC và BD cắt nhau nên hai vectơ $\vec{B D}$ và $\vec{B D}$ không cùng phương. Suy ra hai vec tơ này không cùng hướng và không bằng nhau. Do đó A, B, C sai.

Vì ABCD là hình thang cân nên AC = BD (hai đường chéo bằng nhau). Do đó D đúng.

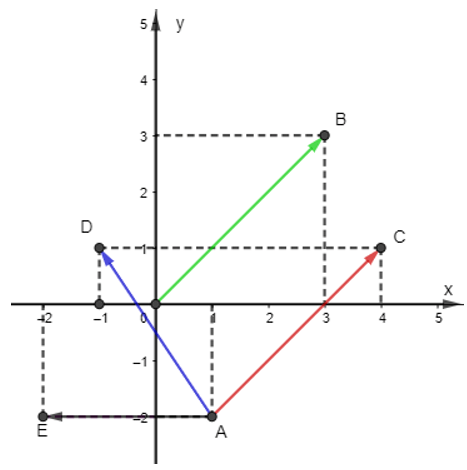
Câu 15. Trên mặt phẳng tọa độ Oxy, hãy vẽ các vec tơ $\vec{O B}$ , $\vec{A C}, \vec{A D}, \vec{A E}$ với A(1; -2), B(3; 3), C(4; 1), D(-1; 1), E(-2; 2). Một vật thể khởi hành từ A và chuyển động thẳng đề với vận tốc biểu diễn bởi vec tơ $\vec{v} = \vec{O B}$ . Hỏi vật thể đó đi qua điểm nào trong các điểm sau?

A. B;

B. C;

C. D;

D. E.

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có hình vẽ sau:

15 Bài tập Các khái niệm mở đầu (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Quan sát hình vẽ, ta thấy: Vec tơ $\vec{O B}$ (màu xanh lá cây) và $\vec{A C}$ (màu đỏ) cùng phương cùng hướng và có độ dài bẳng nhau. Suy ra $\vec{O B} = \vec{A C}$ .