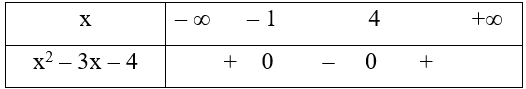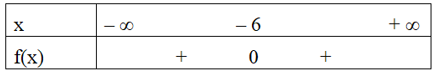Trắc nghiệm Toán 10 Bài 17: Dấu của tam thức bậc hai
Bộ 15 bài tập trắc nghiệm Toán 10 Bài 17: Dấu của tam thức bậc hai có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 17.
Trắc nghiệm Toán 10 Bài 17: Dấu của tam thức bậc hai - Kết nối tri thức
Câu 1. Tìm tất cả các giá trị của a để bất phương trình ax2 – x + a ≥ 0, ∀ x ∈ ℝ
A. a = 0;
B. a < 0;
C. ;
D. ;
Đáp án: D
Giải thích:
ax2 – x + a ≥ 0, ∀ x ∈ ℝ ⇔ ⇔
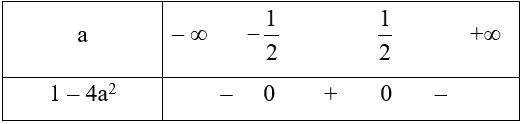
Xét tam thức bậc hai f(a) = 1 – a2, có ∆ = 02 – 4.(-4).1 = 16 > 0. Do đó f(a) có hai nghiệm phân biệt và
Ta có bảng xét dấu
Dựa vào bảng xét dấu ta có 1 – 4a2 ≤ 0
Kết hợp với điều kiện a > 0 suy ra a ∈
Vậy để ax2 – x + a ≥ 0, thì a ∈ hay a ≥
Câu 2. Tam thức y = x2 – 12x – 13 nhận giá trị âm khi và chỉ khi
A. ;
B. ;
C. – 13 < x < 1;
D. – 1 < x < 13;
Đáp án: D
Giải thích:
Xét x2 – 12x – 13 = 0 ⇔
Ta có bảng xét dấu
Dựa vào bảng xét dấu ta có tam thức y = x2 – 12x – 13 nhận giá trị âm khi
– 1 < x < 13.
Câu 3. Tam thức nào sau đây nhận giá trị âm với mọi x < 2
A. y = x2 – 5x + 6 ;
B. y = 16 – x2 ;
C. y = x2 – 2x + 3;
D. y = – x2 + 5x – 6.
Đáp án: D
Giải thích:
Xét đáp án A: y = x2 – 5x +6
Xét x2 – 5x +6 = 0
Ta có bảng xét dấu
Dựa vào bảng xét dấu ta có tam thức y = x2 – 5x + 6 nhận giá trị âm khi 2 < x < 3.
Vậy đáp án A sai.
Xét đáp án B: y = 16 – x2
Xét 16 – x2 = 0 ⇔
Ta có bảng xét dấu
Dựa vào bảng xét dấu ta có tam thức y = 16 – x2 xét trên khoảng (– ∞; 2) nhận giá trị âm khi trên khoảng (– ∞; – 4) nhận giá trị dương trên khoảng (– 4; 2).
Vậy đáp án B sai.
Xét đáp án C: y = x2 – 2x + 3
Xét x2 – 2x + 3 = 0 ⇔ Phương trình vô nghiệm
Ta có bảng xét dấu
Dựa vào bảng xét dấu ta có tam thức y = x2 – 2x + 3 nhận giá trị dương với mọi x ∈ ℝ
Vậy đáp án C sai.
Xét đáp án D: y = – x2 + 5x – 6.
Xét – x2 + 5x – 6 = 0
Ta có bảng xét dấu
Dựa vào bảng xét dấu ta có tam thức y = – x2 + 5x – 6 nhận giá trị âm khi x ∈ (-∞; 2) ∪ (3; +∞)
Vậy đáp án D đúng.
Câu 4. Phương trình x2 – 2(m – 1)x + m – 3 = 0 có hai nghiệm trái dấu nhau khi và chỉ khi
A. m < 3;
B. m < 1;
C. m = 1;
D. 1 < m < 3.
Đáp án: C
Giải thích:
x2 – 2(m – 1)x + m – 3 = 0 có 2 nghiệm đối nhau khi
.
Xét biểu thức m2 – 3m + 4 = + > 0 với mọi m
Vậy phương trình có 2 nghiệm đối dấu khi m = 1.
Câu 5. Phương trình x2 + x + m = 0 vô nghiệm khi và chỉ khi:
A. ;
B. ;
C. ;
D. ;
Đáp án: C
Giải thích:
x2 + x + m = 0 vô nghiệm khi ∆ < 0
Ta có ∆ = 12 – 4.1.m < 0
Câu 6. Các giá trị m làm cho biểu thức f(x) = x2 + 4x + m – 5 luôn dương là:
A. m < 9;
B. m ≥ 9;
C. m > 9;
D. m ∈ ∅
Đáp án: C
Giải thích:
Ta có: f(x) = x2 + 4x + m – 5 luôn luôn dương ⇔ x2 + 4x + m – 5 > 0 với mọi x ∈ ℝ
Câu 7. Cho hàm số f(x) = mx2 – 2mx + m + 1. Giá trị của m để f(x) > 0, ∀ x ∈ ℝ.
A. m ≥ 0 ∀ x ∈ ℝ
B. m > 0
C. m < 0
D. m ≤ 0
Đáp án: A
Giải thích:
TH1. m = 0. Khi đó: f(x) = 1 > 0 .
TH2. m ≠ 0. Khi đó:
f(x) = mx2 – 2mx + m + 1 > 0 ∀ x ∈ ℝ ⇔
Vậy m ≥ 0 thỏa mãn bài toán.
Câu 8. Tập nghiệm của bất phương trình x2 + 4x + 4 > 0 là:
A. (2; + ∞);
B. ℝ;
C. ;
D. ;
Đáp án: C
Giải thích:
Xét x2 + 4x + 4 = 0 x = – 2.
Ta có bảng xét dấu
Dựa vào bảng xét dấu tập nghiệm của bất phương trình là .
Câu 9. Tìm tập xác định của hàm số y = .
A.
B. D = [2; + ∞)
C. D =
D. D =
Đáp án: C
Giải thích:
Hàm số xác định khi và chỉ khi 2x2 – 5x + 2 ≥ 0
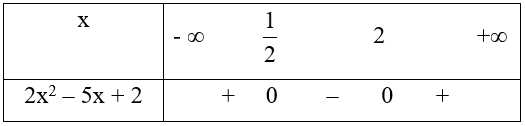
Xét 2x2 – 5x + 2 = 0
Ta có bảng xét dấu
Từ bảng xét dấu ta có 2x2 – 5x + 2 ≥ 0
Câu 10. Tập ngiệm của bất phương trình: x(x + 5) ≤ 2(x2 + 2) là:
A.
B.
C.
D.
Đáp án: A
Giải thích:
Ta có: x(x + 5) ≤ 2(x2 + 2) x2 – 5x + 4 ≥ 0
Đặt f(x) = x2 – 5x + 4 ta có f(x) = 0
Ta có bảng xét dấu :
Dựa vào bảng xét dấu nghiệm của bất phương trình
Câu 11. Bất phương trình: có bao nhiêu nghiệm nguyên dương?
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án: B
Giải thích:
Ta có điều kiện: x2 – 5 ≥ 0
Vậy ⇔ x2 – 3x – 4 < 0.
Xét x2 – 3x – 4 = 0
Ta có bảng xét dấu
Dựa vào bảng xét dấu ta có x2 – 3x – 4 < 0 – 1 < x < 4
Kết hợp với điều kiện ta được: . Suy ra nghiệm nguyên dương của bất phương trình đã cho là: x = 3.
Câu 12. Bảng xét dấu nào sau đây là bảng xét dấu của tam thức f(x) = x2 + 12x + 36 là:
A.
B.
C.
D.
Đáp án: C
Giải thích:
Xét phương trình f(x) = x2 + 12x + 36 = 0 = – 6 và a = 1 > 0.
Ta có bảng xét dấu
Câu 13. Để f(x) = x2 + (m + 1)x +2m + 7 > 0 với mọi x thì
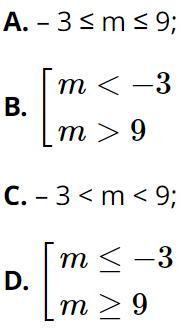
Đáp án: C
Giải thích:
Ta có f(x) > 0 với ∀ x ∈ ℝ
Xét tam thức bậc hai f(m) = m2 – 6m – 27, có ∆’ = 9 – (-27) = 36 > 0. Do đó f(m) có hai nghiệm phân biệt là m = -3 và m = 9.
Ta có bảng xét dấu
Dựa vào bảng xét dấu để ∆ < 0 thì – 3 < m < 9.
Câu 14. Tìm tất cả các giá trị thực của tham số m để bất phương trình
f(x) = (m – 3)x2 + (m + 2)x – 4 > 0 vô nghiệm
A. ;
B. – 22 ≤ m ≤ 2;
C. – 22 < m < 2;
D. ;
Đáp án: B
Giải thích:
Ta có f(x) > 0 vô nghiệm .
Xét m = 3 ta có f(x) = 5x – 4 với thì f(x) > 0 nên m = 3 không thỏa mãn.
Xét m ≠ 3 ta có f(x) ≤ 0 ∀ x ∈ ℝ
Xét tam thức bậc hai (biến m): m2 + 20m – 44 có ∆’ = 102 – (-44) = 144 > 0. Do đó tam thức có hai nghiệm phân biệt x = -22 và x = 2.
Ta có bảng xét dấu
Để f(x) ≤ 0 ∀ x ∈ ℝ
Câu 15. Cho bất phương trình 2x2 – 4x + m + 5 > 0. Tìm m để bất phương trình đúng ∀ x ≥ 3?
A. m ≥ – 11;
B. m > – 11;
C. m < – 11;
D. m < 11;
Đáp án: B
Giải thích:
Ta có: a = 2 > 0. Do đó, 2x2 – 4x + m + 5 > 0, sẽ có trường hợp sau:
Trường hợp 1. ∆ < 0 (– 4)2 – 4.2.(m + 5) < 0 m > – 3, khi đó
2x2 – 4x + m + 5 > 0 với
Do đó 2x2 – 4x + m + 5 > 0 với
Trường hợp 2. ∆ ≥ 0, khi đó phương trình 2x2 – 4x + m + 5 = 0 sẽ có hai nghiệm x1; x2.
Do đó, để 2x2 – 4x + m + 5 > 0 ,
Kết hợp hai trường hợp lại ta được m > – 11 thì thì 2x2 – 4x + m + 5 > 0 với ∀ x ≥ 3.
Các câu hỏi trắc nghiệm Toán 10 sách Kết nối tri thức có đáp án, chọn lọc khác: