Trắc nghiệm Toán 10 Bài 9: Tích của một vectơ với một số

Bộ 15 bài tập trắc nghiệm Toán 10 Bài 9: Tích của một vectơ với một số có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 9.

660

Tải tài liệu

« Trang trước

Trang sau »

Trắc nghiệm Toán 10 Bài 9: Tích của một vectơ với một số - Kết nối tri thức

Câu 1. Cho hình vuông ABCD có cạnh AB = 2 và giao điểm các đường chéo là H. Tính độ dài của vectơ $\vec{A B} + 2 \vec{A H}$ .

A. $\frac{\sqrt{2}}{2}$

B. $\frac{\sqrt{3}}{2}$

C. $\sqrt{5}$

D. $\frac{1}{2}$

Hiển thị đáp án

Đáp án: C

Giải thích:

Vì ABCD là hình bình hành nên AH = HC = $\frac{1}{2}$ AC. Khi đó $\vec{A H} = \frac{1}{2} \vec{A C}$

Ta có: $\vec{A B} + 2 \vec{A H} = \vec{A B} + 2. \frac{1}{2} . \vec{A C} = \vec{A B} + \vec{A C}$

Gọi M là trung điểm của DC

$\Rightarrow \vec{A B} + \vec{A C} = 2 \vec{A M}$

$\Rightarrow \vec{A B} + 2 \vec{A H} = 2 \vec{A M}$

$\Rightarrow |\vec{A B} + 2 \vec{A H}| = 2 |\vec{A M}|$

Xét tam giác ADM vuông tại M, có:

AM² = AD² + DM² = 2² + ${(\frac{2}{2})}^{2}$ = 5 (định lí Py – ta – go)

⇔ AM = $\sqrt{5}$

Vậy $|\vec{A B} + 2 \vec{A H}| = \sqrt{5} .$

Câu 2. Cho vectơ $\vec{a}$ , $\vec{b}$ và hai số thực k, t. Khẳng định nào sau đây là sai?

A. k(t $\vec{a}$ ) = (kt) $\vec{a}$ ;

B. (k + t) $\vec{a}$ = k $\vec{a}$ + t $\vec{b}$ ;

C. k $(\vec{a} + \vec{b})$ = k $\vec{a}$ + k $\vec{b}$ ;

D. (-1) $\vec{a}$ = - $\vec{a}$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có (k + t)

\vec{a}

= k

\vec{a}

+ t

\vec{a}

. Do đó B sai.

Câu 3. Cho ba điểm A, B, C phân biệt sao cho $\vec{A B} = k \vec{A C}$ .Biết rằng C là trung điểm đoạn thẳng AB. Giá trị k thỏa mãn điều kiện nào sau đây?

A. k < 0

B. k = 1

C. 0 < k < 1

D. k > 1

Hiển thị đáp án

Đáp án: D

Giải thích:

15 Bài tập Tích của một vectơ với một số (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Vì C là trung điểm của đoạn thẳng AB nên AC = 2AB.

Ta có $\vec{A C}, \vec{A B}$ là hai vectơ cùng hướng nên $\vec{A C} = 2 \vec{A B}$ . Suy ra k = 2 > 1.

Vậy k thỏa mãn điều kiện k > 1.

Câu 4. Cho hai điểm phân biệt A và B. Xác định ví trí điểm K thỏa mãn $\vec{K A} + 2 \vec{K B} = \vec{0}$ .

A. K là trung điểm của AB

B. K là điểm nằm giữa I và A thỏa mãn IK = $\frac{1}{3}$ IB với I là trung điểm của AB.

C. K là điểm nằm giữa I và B thỏa mãn IK = $\frac{1}{3}$ IB với I là trung điểm của AB.

D. K là điểm nằm giữa I và A thỏa mãn IK = $\frac{1}{3}$ IA với I là trung điểm của AB.

Hiển thị đáp án

Đáp án: C

Giải thích:

Gọi I là trung điểm của đoạn thẳng AB. Khi đó $\vec{I A} + \vec{I B} = \vec{0}$

Xét đẳng thức: $\vec{K A} + 2 \vec{K B} = \vec{0}$

$\Leftrightarrow \vec{K I} + \vec{I A} + 2 (\vec{K I} + \vec{I B}) = \vec{0}$

$\Leftrightarrow 3 \vec{K I} + \vec{I A} + 2 \vec{I B} = \vec{0}$

$\Leftrightarrow 3 \vec{K I} + (\vec{I A} + \vec{I B}) + \vec{I B} = \vec{0}$

$\Leftrightarrow 3 \vec{K I} + \vec{0} + \vec{I B} = \vec{0}$

$\Leftrightarrow \vec{K I} = - \frac{1}{3} \vec{I B}$ hay $\vec{I K} = \frac{1}{3} \vec{I B}$

Vì vậy điểm K là điểm nằm giữa I và B thỏa mãn $I K = \frac{1}{3} I B$

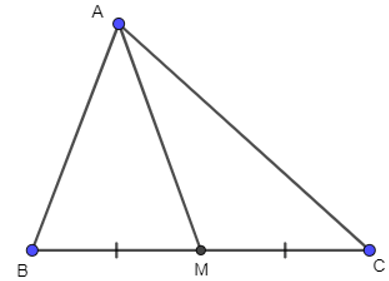
Câu 5. Cho tam giác ABC có đường trung tuyến AM. Khi đó $\vec{A M} = a \vec{A B} + b \vec{A C}$ . Tính S = a + 2b.

A. 1;

B. 2;

C. $\frac{1}{2}$ ;

D. $\frac{3}{2} .$

Hiển thị đáp án

Đáp án: D

Giải thích:

15 Bài tập Tích của một vectơ với một số (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Ta có: $\vec{A B} + \vec{A C} = 2 \vec{A M}$

⇔ $\vec{A M} = \frac{1}{2} \vec{A B} + \frac{1}{2} \vec{A C}$

⇒ a = $\frac{1}{2}$ , b = $\frac{1}{2}$ .

⇒ S = a + 2b = $\frac{1}{2}$ + 2. $\frac{1}{2}$ = $\frac{1}{2}$ + 1 = $\frac{3}{2}$ .

Vậy S = $\frac{3}{2}$ .

Câu 6. Các tam giác ABC có trọng tâm G; M, N lần lượt là trung điểm của BC và AB. Biểu thị $\vec{M G}$ thông qua hai vec tơ $\vec{A B}, \vec{A C}$ .

A. $\vec{N G} = - \frac{1}{6} \vec{A C} + \frac{1}{3} \vec{A B}$ ;

B. $\vec{N G} = - \frac{1}{6} \vec{A B} + \frac{1}{3} \vec{A C}$ ;

C. $\vec{N G} = - \frac{1}{6} \vec{A B} + \frac{1}{6} \vec{A C}$ ;

D. $\vec{N G} = - \frac{1}{6} \vec{A C} + \frac{2}{3} \vec{A B}$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có: $\vec{N G} = \vec{A G} - \vec{A N} = \frac{2}{3} \vec{A M} - \frac{1}{2} \vec{A B}$

$= \frac{2}{3} (\frac{1}{2} \vec{A B} + \frac{1}{2} \vec{A C}) - \frac{1}{2} \vec{A B}$

$= \frac{1}{3} \vec{A B} - \frac{1}{2} \vec{A B} + \frac{1}{2} \vec{A C}$

$= - \frac{1}{6} \vec{A B} + \frac{1}{2} \vec{A C}$ .

Vậy $\vec{N G} = - \frac{1}{6} \vec{A B} + \frac{1}{3} \vec{A C}$ .

Câu 7. Cho tam giác ABC có G là trọng tâm tam giác. Hãy xác định điểm M để $\vec{M A} + \vec{M B} + 2 \vec{M C} = \vec{0}$ .

A. M là trung điểm của đoạn thẳng GC;

B. M nằm giữa G và C sao cho GM = 4GC;

C. M nằm ngoài G và C sao cho GM = 4GC;

D. M nằm giữa G và C sao cho $G M = \frac{1}{4} G C$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Vì G là trọng tâm tam giác ABC nên $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ .

Xét $\vec{M A} + \vec{M B} + 2 \vec{M C} = \vec{0}$

$\Leftrightarrow \vec{M G} + \vec{G A} + \vec{M G} + \vec{G B} + 2 (\vec{M G} + \vec{G C}) = \vec{0}$

$\Leftrightarrow 4 \vec{M G} + (\vec{G A} + \vec{G B} + \vec{G C}) + \vec{G C} = \vec{0}$

$\Leftrightarrow 4 \vec{M G} + \vec{G C} = \vec{0}$

$\Leftrightarrow 4 \vec{M G} = - \vec{G C}$

$\Leftrightarrow \vec{G M} = \frac{1}{4} \vec{G C}$ .

Vậy G là điểm nằm giữa G và C sao cho $G M = \frac{1}{4} G C$ .

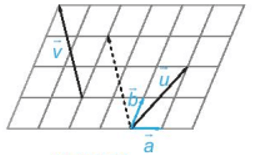
Câu 8. Trong hình vẽ, hãy biểu thị mỗi vectơ $\vec{u}, \vec{v}$ hai vectơ $\vec{a}, \vec{b}$ , tức là tìm các số x, y, z, t để $\vec{u} = x \vec{a} + y \vec{b}, \vec{v} = t \vec{a} + z \vec{b} .$

15 Bài tập Tích của một vectơ với một số (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

A. x = 1, y = 2, z = 2, t = -1;

B. x = 1, y = 2, z = -2, t = 3;

C. x = 1, y = 2, z = -2, t = -1;

D. x = 1, y = -2, z = 2, t = -3.

Hiển thị đáp án

Đáp án: B

Giải thích:

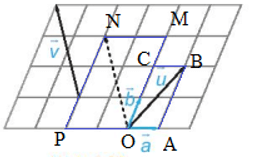
Ta có hình vẽ sau:

15 Bài tập Tích của một vectơ với một số (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Xét hình bình hành OABC, có:

$\vec{O A} = \vec{a}, \vec{O C} = 2 \vec{b}, \vec{O B} = \vec{u}$

Khi đó, ta có:

$\vec{u} = \vec{O B} = \vec{O A} + \vec{O C} = \vec{a} + 2 \vec{b}$ (quy tắc hình bình hành)

Xét hình bình hành OMNP, có:

$\vec{O N} = \vec{v}, \vec{O M} = 3 \vec{b}, \vec{O P} = - 2 \vec{a}$

Khi đó, ta có:

$\vec{v} = \vec{O N} = \vec{O M} + \vec{O P} = 3 \vec{b} - 2 \vec{a} = - 2 \vec{a} + 3 \vec{b} .$

Vậy $\vec{u} = \vec{a} + 2 \vec{b}, \vec{v} = - 2 \vec{a} + 3 \vec{b} .$

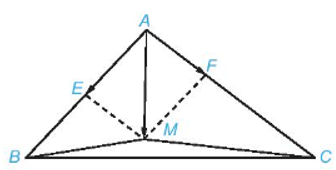
Câu 9. Cho tam giác ABC . Lấy E là trung điểm của AB và F thuộc cạnh AC sao cho AF = $\frac{1}{3}$ AC. Hãy xác định điểm M để $\vec{M A} + 3 \vec{M B} + 2 \vec{M C} = \vec{0}$ .

A. M là trung điểm BC;

B. M là đỉnh hình chữ nhật AEFM;

C. M là đỉnh hình bình hành EAFM;

D. M là đỉnh tam giác đều BEM.

Hiển thị đáp án

Đáp án: C

Giải thích:

15 Bài tập Tích của một vectơ với một số (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Để xác định vị trí điểm M, trước hết ta biểu thị $\vec{A M}$ (với gốc A đã biết) theo hai vec tơ $\vec{A B}, \vec{A C}$ .

Đẳng thức vec tơ đã cho tương đương với $\vec{M A} + 3 (\vec{M A} + \vec{A B}) + 2 (\vec{M A} + \vec{A C}) = \vec{0}$

$\Leftrightarrow 6 \vec{M A} + 3 \vec{A B} + 2 \vec{A C} = \vec{0}$

$\Leftrightarrow \vec{A M} = \frac{1}{2} \vec{A B} + \frac{1}{3} \vec{A C}$ .

Vì E là trung điểm của AB và F thuộc cạnh AC sao cho AF = $\frac{1}{3}$ AC nên $\vec{A E} = \frac{1}{2} \vec{A B}$ và $\vec{A F} = \frac{1}{3} \vec{A C}$ .

Vì vậy $\vec{A M} = \vec{A E} + \vec{A F}$ .

Suy ra M là đỉnh thứ tư của hình bình hành EAFM.

Câu 10. Biết rằng hai vectơ $\vec{a}$ và $\vec{b}$ không cùng phương nhưng hai vectơ $5 x \vec{a} + 4 \vec{b}$ và $(3 x - 2) \vec{a} - 2 \vec{b}$ cùng phương. Khi đó giá trị của x bằng:

A. $\frac{4}{11}$ ;

B. $\frac{2}{3}$ ;

C. 4;

D. -4.

Hiển thị đáp án

Đáp án: A

Giải thích:

Vectơ $5 x \vec{a} + 4 \vec{b}$ và $(3 x - 2) \vec{a} - 2 \vec{b}$ cùng phương khi 5x = - 2(3x – 2)

⇔ 5x = -6x + 4

⇔ 11x = 4

⇔ x = $\frac{4}{11}$ .

Vậy x = $\frac{4}{11}$ .

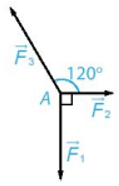
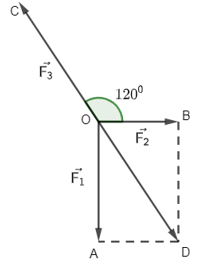
Câu 11. Chất điểm A chịu tác động của ba lực $\vec{F_{1}}, \vec{F_{2}}, \vec{F_{3}}$ như hình vẽ và ở trạng thái cân bằng (tức là $\vec{F_{1}} + \vec{F_{2}} + \vec{F_{3}} = \vec{0}$ ). Tính độ lớn của các lực $\vec{F_{2}}, \vec{F_{3}},$ biết $\vec{F_{1}}$ có độ lớn là 20N.

15 Bài tập Tích của một vectơ với một số (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

A. $|\vec{F_{1}}| = \frac{20}{\sqrt{3}} N, |\vec{F_{2}}| = \frac{40 \sqrt{3}}{3} N;$

B. $F_{1} | = = \frac{40}{\sqrt{3}} N | \vec{F_{2}} | = \frac{20 \sqrt{3}}{3}; N$

C. $|\vec{F_{1}}| = |\vec{F_{2}}| = \frac{40 \sqrt{3}}{3} N;$

D. $|\vec{F_{1}}| = \frac{60}{\sqrt{3}} N, |\vec{F_{2}}| = \frac{40 \sqrt{3}}{3} N .$

Hiển thị đáp án

Đáp án: A

Giải thích:

15 Bài tập Tích của một vectơ với một số (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Ta có: $\vec{F_{1}} + \vec{F_{2}} + \vec{F_{3}} = \vec{0}$

$\Leftrightarrow \vec{F_{1}} + \vec{F_{2}} = - \vec{F_{3}}$

Mà $\vec{F_{1}} + \vec{F_{2}} = \vec{O A} + \vec{O B} = \vec{O D}$ (OBDA là hình bình hành)

$\Rightarrow \vec{O D} = - \vec{F_{3}}$

⇒ Hai vecto $\vec{O D}$ và $\vec{F_{3}}$ là hai vecto đối nhau

$\Rightarrow |\vec{O D}| = |- \vec{F_{3}}|$ và $\hat{B O D} = 60^{0}$ .

Ta lại có: $\vec{B D} = \vec{F_{1}}$

Xét ΔOBD, có:

$O B = \frac{B D}{\tan 60^{0}} = \frac{20}{\sqrt{3}} (N) \Rightarrow |\vec{F_{2}}| = \frac{20}{\sqrt{3}} N .$

$O D = \frac{B D}{\sin 60^{0}} = \frac{40 \sqrt{3}}{3} (N) \Rightarrow |\vec{F_{3}}| = \frac{40 \sqrt{3}}{3} N .$

Vậy độ lớn vecto $\vec{F_{2}}, \vec{F_{3}}$ lần lượt là $\frac{20}{\sqrt{3}} N, \frac{40 \sqrt{3}}{3} N .$

Câu 12. Cho vectơ $\vec{a} \neq \vec{0}$ với số thực k như thế nào thì vectơ $k \vec{a}$ ngược hướng với vectơ $\vec{a}$ .

A. k = 1;

B. k = 0;

C. k < 0;

D. k > 0.

Hiển thị đáp án

Đáp án: C

Giải thích:

Tích của một vectơ

\vec{a} \neq \vec{0}

với số thực k < 0 là một vec tơ kí hiệu

k \vec{a}

ngược hướng với vectơ

\vec{a}

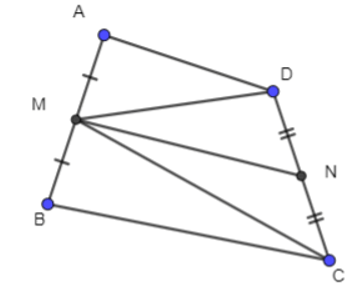
Câu 13. Cho tứ giác ABCD. Gọi M là trung điểm của cạnh AB, CD. Đẳng thức nào dưới đây là sai?

A. $\vec{B C} + \vec{A D} = \vec{M N}$ ;

B. $\vec{B C} + \vec{A D} = 2 \vec{M N}$ ;

C. $\vec{B C} + \vec{A D} = 3 \vec{M N}$ ;

D. $\vec{B C} + \vec{A D} = 4 \vec{M N}$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

15 Bài tập Tích của một vectơ với một số (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Ta có $\vec{B C} + \vec{A D} = \vec{B M} + \vec{M C} + \vec{A M} + \vec{M D}$

$= (\vec{B M} + \vec{A M}) + (\vec{M C} + \vec{M D})$

$= \vec{0} + 2 \vec{M N}$

$= 2 \vec{M N}$

Vậy $\vec{B C} + \vec{A D} = 2 \vec{M N}$

Câu 14. Cho hai vectơ $\vec{a}$ và $\vec{b}$ khác vec tơ – không. Hai vec tơ nào dưới đây cùng phương?

A. $2 \vec{a} + \vec{b}$ và $\frac{1}{3} \vec{a} - \frac{1}{2} \vec{b}$ ;

B. $- \vec{a} + \vec{b}$ và $- 2 \vec{a} + 3 \vec{b}$ ;

C. $\frac{1}{6} \vec{a} - \vec{b}$ và $- \vec{a} + 6 \vec{b}$ ;

D. $\vec{a} + \vec{b}$ và $\vec{a} - \vec{b}$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có:

- 6 (\frac{1}{6} \vec{a} - \vec{b}) = - \vec{a} + \vec{b}

. Do đó vectơ

\frac{1}{6} \vec{a} - \vec{b}

và

- \vec{a} + 6 \vec{b}

cùng phương.

Câu 15. Cho hình vẽ sau:

15 Bài tập Tích của một vectơ với một số (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 10

Phát biểu nào dưới đây là đúng?

A. $5 \vec{M P} = 4 \vec{M N}$ ;

B. $\vec{P M} = 4 \vec{P N}$ ;

C. $\vec{P N} = - \frac{1}{5} \vec{M N}$ ;

D. Cả A, B và C đều sai

Hiển thị đáp án

Đáp án: A

Giải thích:

+) Ta có hai vectơ $\vec{M P}$ và $\vec{M N}$ cùng hướng và $M P = \frac{4}{5} M N$ . Suy ra $\vec{M P} = \frac{4}{5} \vec{M N}$ hay $5 \vec{M P} = 4 \vec{M N}$ . Do đó A đúng.

+) Ta có hai vectơ $\vec{P M}$ và $\vec{P N}$ ngược hướng và PM = 4PN. Suy ra $\vec{P M} = - 4 \vec{P N}$ . Do đó B sai.

+) Ta có hai vectơ $\vec{P N}$ và $\vec{M N}$ cùng hướng và $P N = \frac{1}{5} M N$ . Suy ra $P N = \frac{1}{5} M N$ . Do đó D sai.

Các câu hỏi trắc nghiệm Toán 10 sách Kết nối tri thức có đáp án, chọn lọc khác:

660

Tải tài liệu

« Trang trước

Trang sau »

Trắc nghiệm Toán 10 Bài 9: Tích của một vectơ với một số

Có thể bạn quan tâm