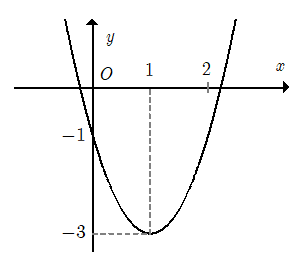Trắc nghiệm Toán 10 Bài 16: Hàm số bậc hai

Bộ 15 bài tập trắc nghiệm Toán 10 Bài 16: Hàm số bậc hai có đáp án đầy đủ gồm các câu hỏi trắc nghiệm đầy đủ các mức độ nhận biết, thông hiểu, vận dụng, vận dung cao sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 10 Bài 16.

471

Tải tài liệu

« Trang trước

Trang sau »

Trắc nghiệm Toán 10 Bài 16: Hàm số bậc hai - Kết nối tri thức

Câu 1. Cho hàm số y = f(x). Biết f(x + 2) = x² – 3x + 2 thì f(x) bằng:

A. y = f(x) = x² + 7x – 12;

B. y = f(x) = x² – 7x – 12;

C. y = f(x) = x² + 7x + 12;

D. y = f(x) = x² – 7x + 12.

Hiển thị đáp án

Đáp án: D

Giải thích:

Đặt x + 2 = t ⇔ x = t – 2

Khi đó, ta có f(t) = (t – 2)² – 3(t – 2) + 2 = t² – 7t + 12

Vậy f(x) = x² – 7x + 12.

Câu 2. Tọa độ đỉnh I của hàm số y = – 3x² + 4x – 1

A. $I (- \frac{2}{3}; \frac{1}{3})$

B. $I (\frac{2}{3}; \frac{1}{3})$

C. $I (\frac{4}{3}; - 1)$

D. $I (\frac{2}{3}; \frac{4}{3})$

Hiển thị đáp án

Đáp án: B

Giải thích:

Tọa độ đỉnh $I (- \frac{b}{2a}; - \frac{Δ}{4a})$

Ta có giá trị $- \frac{b}{2 a} = - \frac{4}{2. (- 3)} = \frac{2}{3}$

giá trị $- \frac{Δ}{4 a} = - \frac{4^{2} - 4. (- 3) . (- 1)}{4. (- 3)} = \frac{1}{3}$

Vậy toạ độ đỉnh I $(\frac{2}{3}; \frac{1}{3})$

Câu 3. Cho hàm số y = 2x² – 4x – 1. Kết luận nào đúng trong các kết luận sau

A. Hàm số đồng biến trên khoảng (0; + ∞);

B. Hàm số đồng biến trên khoảng (– ∞; 1);

C. Hàm số nghịch biến trên khoảng (– ∞; 0);

D. Hàm số nghịch biến trên khoảng (– ∞; 2).

Hiển thị đáp án

Đáp án: C

Giải thích:

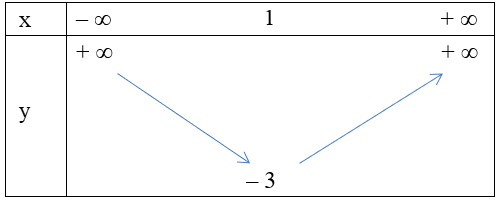
Tọa độ đỉnh của hàm số là I(1; – 3)

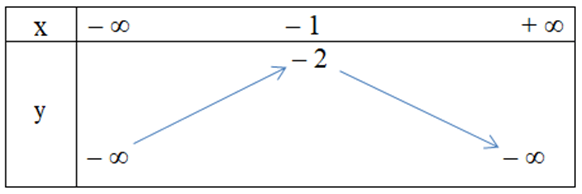
Bảng biến thiên

15 Bài tập Hàm số bậc hai (Trắc nghiệm Toán lớp 10 có đáp án) | Kết nối tri thức

Từ bảng biến thiên ta có hàm số nghịch biến trên khoảng (– ∞; 1) nên cũng nghịch biến trên khoảng (– ∞; 0).

Câu 4. Cho parabol y = ax² + bx – 3. Xác định hệ số a, b biết parabol có đỉnh

I(– 1; – 5)

A. a = 1; b = 2;

B. a = 1; b = – 2;

C. a = – 2; b = 4;

D. a = 2; b = 4.

Hiển thị đáp án

Đáp án: D

Giải thích:

Tọa độ đỉnh của parabol là $I (- \frac{b}{2a}; - \frac{Δ}{4a})$

Ta có

$\{\begin{cases} - \frac{b}{2 a} = - 1 \\ - \frac{b^{2} - 4 a c}{4 a} = - 5 \\ a \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} b = 2 a \\ 4 a^{2} - 8 a = 0 \\ a \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} b = 2 a \\ [\begin{array}{l} a = 0 \\ a = 2 \end{array} \\ a \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} a = 2 \\ b = 4 \end{cases}$

Vậy a = 2 và b = 4.

Câu 5. Hàm số y = – x² + 2x + 1 đồng biến trên khoảng

A. (– ∞; + ∞);

B. (– ∞; 1);

C. (1; + ∞);

D. (– ∞; 2).

Hiển thị đáp án

Đáp án: B

Giải thích:

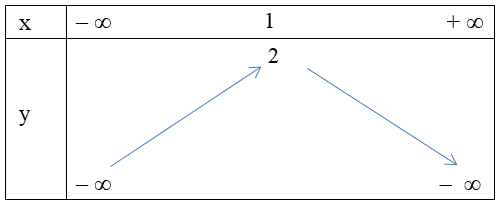
Tọa độ đỉnh của hàm số là I(1; 2)

Bảng biến thiên

15 Bài tập Hàm số bậc hai (Trắc nghiệm Toán lớp 10 có đáp án) | Kết nối tri thức

Từ bảng biến thiên ta có hàm số tăng từ trái sang phải trên khoảng (– ∞; 1) nên hàm số đồng biến trên khoảng (– ∞; 1).

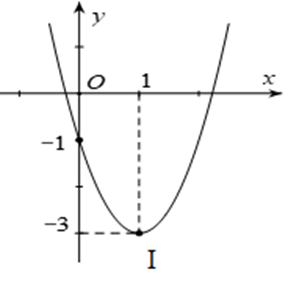
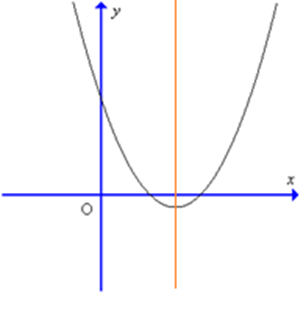
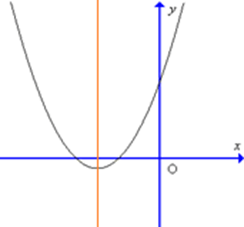
Câu 6. Cho parabol có đồ thị như hình sau:

15 Bài tập Hàm số bậc hai (Trắc nghiệm Toán lớp 10 có đáp án) | Kết nối tri thức

Tọa độ đỉnh I của parabol

A. I(– 1; – 3);

B. I(1; 0);

C. I(0; – 3);

D. I(1; – 3).

Hiển thị đáp án

Đáp án: D

Giải thích:

Từ đồ thị suy ra tọa độ đỉnh của hàm số là I(1; – 3).

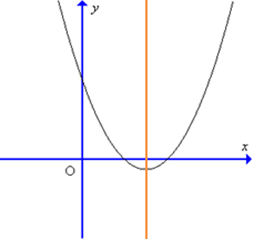
Câu 7. Cho hàm số y = f(x) có đồ thị như hình sau:

15 Bài tập Hàm số bậc hai (Trắc nghiệm Toán lớp 10 có đáp án) | Kết nối tri thức

Hàm số đồng biến trên khoảng

A. $(- \infty; - \frac{3}{2})$

B. $(- \infty; - \frac{25}{4})$

C. $(- \frac{3}{2} : + \infty)$

D. $(- \frac{25}{4}; + \infty)$

Hiển thị đáp án

Đáp án: C

Giải thích:

Đồ thị hàm số đi lên từ trái qua phải trên khoảng

(- \frac{3}{2}; + \infty)

nên hàm số đồng biến trên khoảng

(- \frac{3}{2}; + \infty)

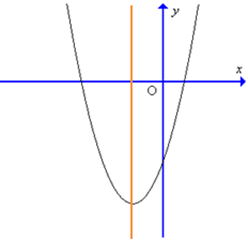
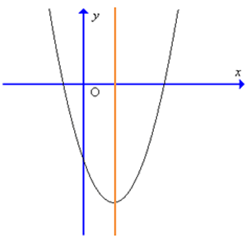
Câu 8. Cho hàm số y = ax² + bx + c có đồ thị như hình sau:

15 Bài tập Hàm số bậc hai (Trắc nghiệm Toán lớp 10 có đáp án) | Kết nối tri thức

Kết luận nào sau đây đúng về hệ số a, b:

A. a > 0; b > 0;

B. a < 0; b > 0;

C. a > 0; b < 0;

D. a > 0; c <0.

Hiển thị đáp án

Đáp án: C

Giải thích:

Vì bề lõm của đồ thị hướng lên trên nên a > 0;

Trục đối xứng của hàm số (đường màu đỏ) nằm bên phải trục Oy nên ta có trục đối xứng nhận giá trị dương hay $x = - \frac{b}{2 a} > 0$ mà a > 0 nên b < 0.

Vậy a > 0 và b < 0.

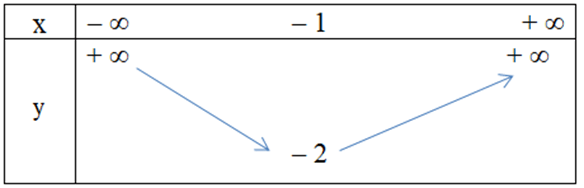
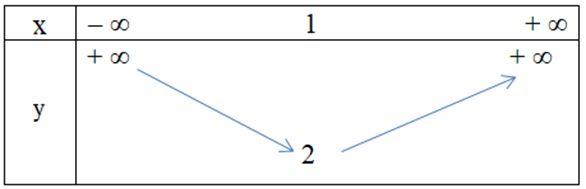
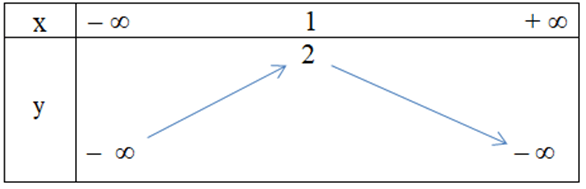
Câu 9. Hàm số y = x² + 2x – 1 có bảng biến thiên là

B. 15 Bài tập Hàm số bậc hai (Trắc nghiệm Toán lớp 10 có đáp án) | Kết nối tri thức

Hiển thị đáp án

Đáp án: A

Giải thích:

Tọa độ đỉnh của hàm số là I(– 1; – 2)

Vì hệ số a > 0 nên hàm số đồng biến trên khoảng (– 1; + ∞) và nghịch biến trên khoảng (– ∞; – 1) ta có bảng biến thiên

15 Bài tập Hàm số bậc hai (Trắc nghiệm Toán lớp 10 có đáp án) | Kết nối tri thức

Câu 10. Đồ thị hàm số y = 4x² – 3x – 1 có dạng nào trong các dạng sau đây?

Hiển thị đáp án

Đáp án: D

Giải thích:

Giao điểm của đồ thị với trục tung tại A(0; – 1) nên đồ hàm số cắt trục tung tại điểm có tung độ âm. Do đó chỉ có hình C và hình D thỏa mãn.

Hàm số có trục đối xứng $x = \frac{3}{8} > 0$ nên trục đối xứng nằm về phần dương của trục Ox.

Do đó hình D là hình vẽ đúng.

Câu 11. Parabol y = ax² + bx + c đạt giá trị nhỏ nhất bằng 4 tại x = – 2 và đi qua

A(0; 6) có phương trình là

A. $y = \frac{1}{2} x^{2} + 2 x + 6$

B. y = x² + 2x + 6

C. y = $\frac{1}{2}$ x² + 6x + 6

D. y = x² + x + 4

Hiển thị đáp án

Đáp án: A

Giải thích:

Parabol y = ax² + bx + c đạt giá trị nhỏ nhất bằng 4 tại x = – 2 và đi qua A(0; 6) nên ta có hệ phương trình sau:

$\{\begin{cases} a > 0 \\ \frac{- b}{2 a} = - 2 \\ a . {(- 2)}^{2} - 2 b + c = 4 \\ a {.0}^{2} + 0. b + c = 6 \end{cases} \Leftrightarrow \{\begin{cases} a > 0 \\ 4 a - b = 0 \\ 4 a - 2 b + c = 4 \\ c = 6 \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{1}{2} \\ b = 2 \\ c = 6 \end{cases}$

Vậy $y = \frac{1}{2} x^{2} + 2 x + 6$ .

Câu 12. Trục đối xứng của parabol y = x² – 4x + 1

A. x = 2

B. x = – 2

C. x = 4

D. x = – 4

Hiển thị đáp án

Đáp án: A

Giải thích:

Trục đối xứng

x = - \frac{b}{2a} = - \frac{- 4}{2} = 2

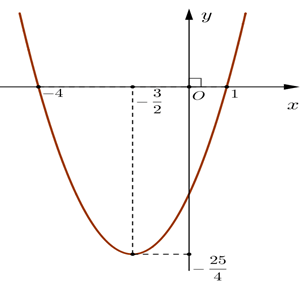
Câu 13. Cho hàm số y = ax² + bx + c có đồ thị như hình dưới đây. Hàm số đó là hàm số nào?

15 Bài tập Hàm số bậc hai (Trắc nghiệm Toán lớp 10 có đáp án) | Kết nối tri thức

A. y = x² – 4x – 1;

B. y = 2x² – 4x – 1;

C. y = – 2x² – 4x – 1;

D. y = 2x² – 4x + 1.

Hiển thị đáp án

Đáp án: B

Giải thích:

Nhận xét:

Parabol có bề lõm hướng lên vậy a > 0. Loại đáp án C

Parabol giao trục tung tại A(0; – 1). Loại đáp án D

Parabol có trục đối xứng x = 1.

Xét đáp án A hàm số có trục đối xứng x = 2. Loại đáp án A

Đáp án B có trục đối xứng x = 1

Câu 14. Biết rằng P: y = ax² + bx + 2 (a > 1) đi qua điểm M(–1; 6) và có tung độ đỉnh bằng $- \frac{1}{4}$ . Tính tích P = a.b.

A. P = – 3

B. P = – 2

C. P = 192

D. P = 28

Hiển thị đáp án

Đáp án: C

Giải thích:

Vì P đi qua điểm M(– 1; 6) và có tung độ đỉnh bằng $- \frac{1}{4}$ nên ta có hệ

$\{\begin{cases} a - b + 2 = 6 \\ - \frac{Δ}{4 a} = - \frac{1}{4} \end{cases} \Leftrightarrow \{\begin{cases} a - b = 4 \\ b^{2} - 4 a c = a \end{cases}$

$\Leftrightarrow \{\begin{cases} a = 4 + b \\ b^{2} - 8 (4 + b) = 4 + b \end{cases} \Leftrightarrow \{\begin{cases} a = 4 + b \\ b^{2} - 9 b - 36 = 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} a = 16 \\ b = 12 \end{cases}$ (thỏa mãn a > 1) $\{\begin{cases} a = 1 \\ b = - 3 \end{cases}$ hoặc (loại).

Suy ra P = a.b = 16.12 = 192.

Câu 15. Biết rằng hàm số y = ax² + bx + c (a ≠ 0) đạt cực đại bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A(0; – 1). Tính tổng S = a + b + c.

A. S = – 1;

B. S = – 4;

C. S = 4;

D. S = 2.

Hiển thị đáp án

Đáp án: D

Giải thích:

Vì hàm số đạt cực đại tại x = 2 nên bề lõm của parabol quay xuống dưới, do đó a < 0.

Từ giả thiết ta có hệ

$\{\begin{cases} - \frac{b}{2 a} = 2 \\ - \frac{Δ}{4 a} = 3 \\ c = - 1 \end{cases} \Leftrightarrow \{\begin{cases} b = - 4 a \\ b^{2} - 4 a c = - 12 a \\ c = - 1 \end{cases} \Leftrightarrow \{\begin{cases} b = - 4 a \\ 16 a^{2} + 16 a = 0 \\ c = - 1 \end{cases}$

$\Leftrightarrow \{\begin{cases} a = 0 \\ b = 0 \\ c = - 1 \end{cases}$ (loại) hoặc $\{\begin{cases} a = - 1 \\ b = 4 \\ c = - 1 \end{cases}$ (thỏa mãn)